МО. Решение данной задачи методом перебора
 Скачать 164.74 Kb. Скачать 164.74 Kb.
|
|
Дана функция вида 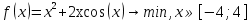 , необходимо найти минимум данной функции методом перебора. , необходимо найти минимум данной функции методом перебора.Рассмотрим решение данной задачи методом перебора. Метод перебора или равномерного поиска является простейшим из прямых методов оптимизации и состоит в следующем. Разобьем отрезок 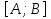 , на , на 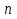 равных частей точками деления равных частей точками деления 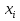 , где , где 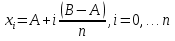 . .Вычислив значения 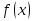 , в точках , в точках 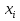 путем сравнения найдем точку путем сравнения найдем точку 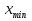 , где , где 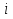 - это число от 0 до - это число от 0 до 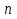 , такую, что , такую, что 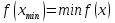 Погрешность определения точки минимума 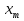 функции методом перебора не превосходит величины функции методом перебора не превосходит величины 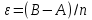 . .Реализуем программу для данного алгоритма с исходными данными задачи с предоставлением пользователю возможности выбора значения 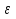 . Программу реализуем в консольном виде на языке программирования Си. Блок схема программы представлена на изображение №1, а код программы представлен в листинге №1. Результат работы программы для . Программу реализуем в консольном виде на языке программирования Си. Блок схема программы представлена на изображение №1, а код программы представлен в листинге №1. Результат работы программы для 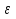 .=0.01 представлен на изображение №2. .=0.01 представлен на изображение №2. Листинг №1.
Изображение №2 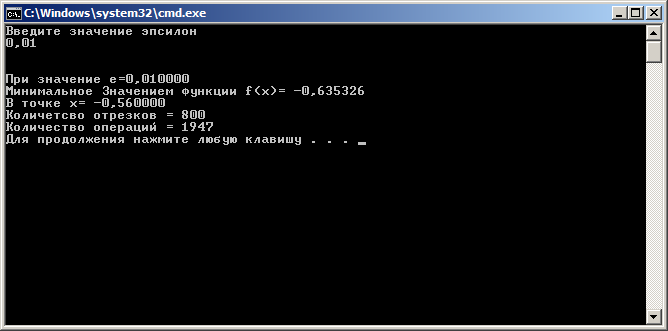 Дана функция вида 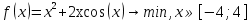 , необходимо найти минимум данной функции методом средней точки. , необходимо найти минимум данной функции методом средней точки.Суть метода средней точки основывается на алгоритме исключения интервалов, на каждой итерации которого рассматривается одна пробная точка R на интервале 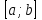 . . Рассмотрим алгоритм поиска минимума функции методом средней точки. Пусть в интервале [a,b] имеются две точки A и B, в которых производные 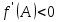 и и 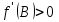 . Оптимальная точка R расположена между A и B. . Оптимальная точка R расположена между A и B.Шаг 1. Положить A=a, B=b, причем 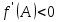 и и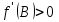 , ,Шаг 2. Вычисляем среднюю точку интервала 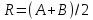 Шаг 3. Вычисляем значение 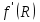 Шаг 4. Если 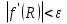 , то закончить поиск. В противном случае, если , то закончить поиск. В противном случае, если 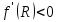 , положить A=R, и перейти к шагу 2, , положить A=R, и перейти к шагу 2,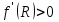 , положить B=R и перейти к шагу 2. , положить B=R и перейти к шагу 2.Как следует из алгоритма процедура поиска по методу средней точки происходит до тех пор, пока не будет найдена точка R удовлетворяющая условию 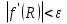 и как следствие условию и как следствие условию 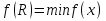 . .Реализуем программу для данного алгоритма с исходными данными задачи с предоставлением пользователю возможности выбора значения 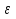 . Программу реализуем в консольном виде на языке программирования Си. Блок схема программы представлена на изображение №, а код программы представлен в листинге №2. Результат работы программы для . Программу реализуем в консольном виде на языке программирования Си. Блок схема программы представлена на изображение №, а код программы представлен в листинге №2. Результат работы программы для 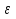 .=0.01 представлен на изображение №3. .=0.01 представлен на изображение №3.
Изображение №3. 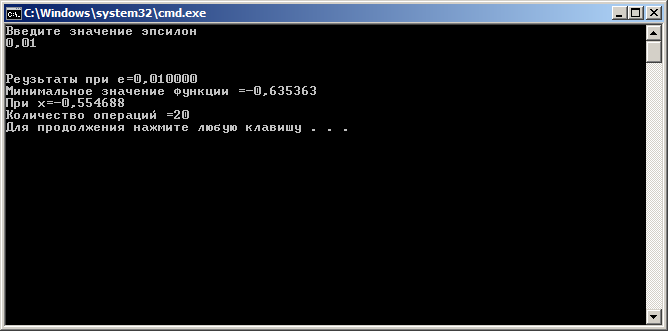 Рассмотрим сравнительную таблицу зависимости количества вычислений для разных параметров 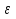 , для обоих видов алгоритмов. , для обоих видов алгоритмов.
Задание №2. Решить задачу линейного программирования, используя симплекс-метод. 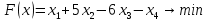 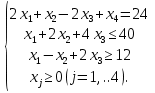 Определим минимальное значение целевой функции F(X) = x1+5x2-6x3-x4 при следующих условиях-ограничений. Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≥) вводим базисную переменную x6 со знаком минус. 2x1+x2-2x3+x4 = 24 x1+2x2+4x3+x5 = 40 x1-x2+2x3-x6 = 12 Расширенная матрица системы ограничений-равенств данной задачи:
Приведем систему к единичной матрице методом жордановских преобразований. 1. В качестве базовой переменной можно выбрать x4. 2. В качестве базовой переменной можно выбрать x5. 3. В качестве базовой переменной можно выбрать x6. Получаем новую матрицу:
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,5,6). Выразим базисные переменные через остальные: x4 = -2x1-x2+2x3+24 x5 = -x1-2x2-4x3+40 x6 = x1-x2+2x3-12 Подставим их в целевую функцию: F(X) = x1+5x2-6x3-(-2x1-x2+2x3+24) или F(X) = 3x1+6x2-8x3-24 Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным. Вместо переменной x6 следует ввести переменную x3. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
Выразим базисные переменные через остальные: x4 = -3x1+x6+36 x5 = x1-4x2-2x6+16 x3 = -1/2x1+1/2x2+1/2x6+6 Подставим их в целевую функцию: F(X) = x1+5x2-6(-1/2x1+1/2x2+1/2x6+6)-(-3x1+x6+36) или F(X) = 7x1+2x2-4x6-72 3x1+x4-x6=36 -x1+4x2+x5+2x6=16 1/2x1-1/2x2+x3-1/2x6=6 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x4, x5, x3 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,6,36,16,0). Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план не оптимален, так как в индексной строке находятся положительные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x6, так как это наибольший коэффициент. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai6 и из них выберем наименьшее: min (- , 16 : 2 , - ) = 8 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.
4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x6. Строка, соответствующая переменной x6 в плане 1, получена в результате деления всех элементов строки x5 плана 0 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x6 записываем нули. Таким образом, в новом плане 1 заполнены строка x6 и столбец x6. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (2), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
1. Проверка критерия оптимальности. Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 0, x2 = 0, x3 = 10, x4 = 44 F(X) = 1•0 + 5•0 -6•10 -1•44 = -104 Ответ: минимальное значение функция принимает при x1 = 0, x2 = 0, x3 = 10, x4 = 44. Проверяем результат решения задачи в MS Excel с помощью надстроки «Поиск решений». Результат расчетов представлены на рисунке №4. Рисунок №4. 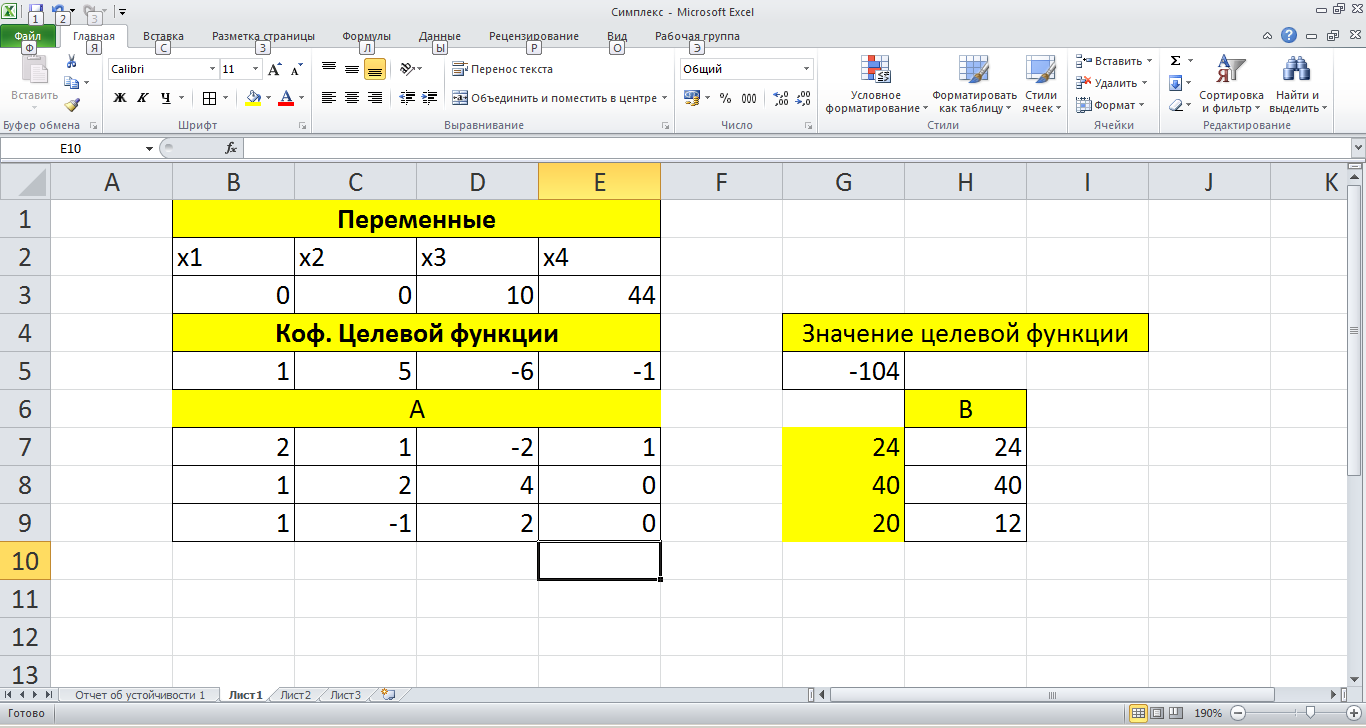 Уфимский государственный авиационный технический университет Кафедра АСУ Пояснительная записка к расчетно-графической работе по дисциплине «Методы оптимизации» Вариант №38. Выполнил: Студент группы ПИ-404з Муллагалимов Р.Ф. Проверил: __________ Абдулнагимов А.И. «___»__________ Уфа 2018г. |
