Задачи линейного программирования. ЛП. Решите графическим методом задачу линейного программирования
 Скачать 2.53 Mb. Скачать 2.53 Mb.
|
Вариант 5Задание 1. Решите графическим методом задачу линейного программирования (x1≥0, x2≥0). Провести анализ на чувствительность 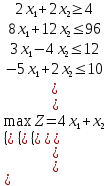 Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). Построим уравнение 2x1+2x2 = 4 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 2. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 2. Соединяем точку (0;2) с (2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:2 • 0 + 2 • 0 - 4 ≤ 0, т.е. 2x1+2x2 - 4≥ 0 в полуплоскости выше прямой. Построим уравнение 8x1+12x2 = 96 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 8. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 12. Соединяем точку (0;8) с (12;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:8 • 0 + 12 • 0 - 96 ≤ 0, т.е. 8x1+12x2 - 96≤ 0 в полуплоскости ниже прямой. Построим уравнение 3x1-4x2 = 12 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = -3. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 4. Соединяем точку (0;-3) с (4;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:3 • 0 - 4 • 0 - 12 ≤ 0, т.е. 3x1-4x2 - 12≤ 0 в полуплоскости ниже прямой. Построим уравнение -5x1+2x2 = 10 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 5. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = -2. Соединяем точку (0;5) с (-2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:-5 • 0 + 2 • 0 - 10 ≤ 0, т.е. -5x1+2x2 - 10≤ 0 в полуплоскости ниже прямой.  или 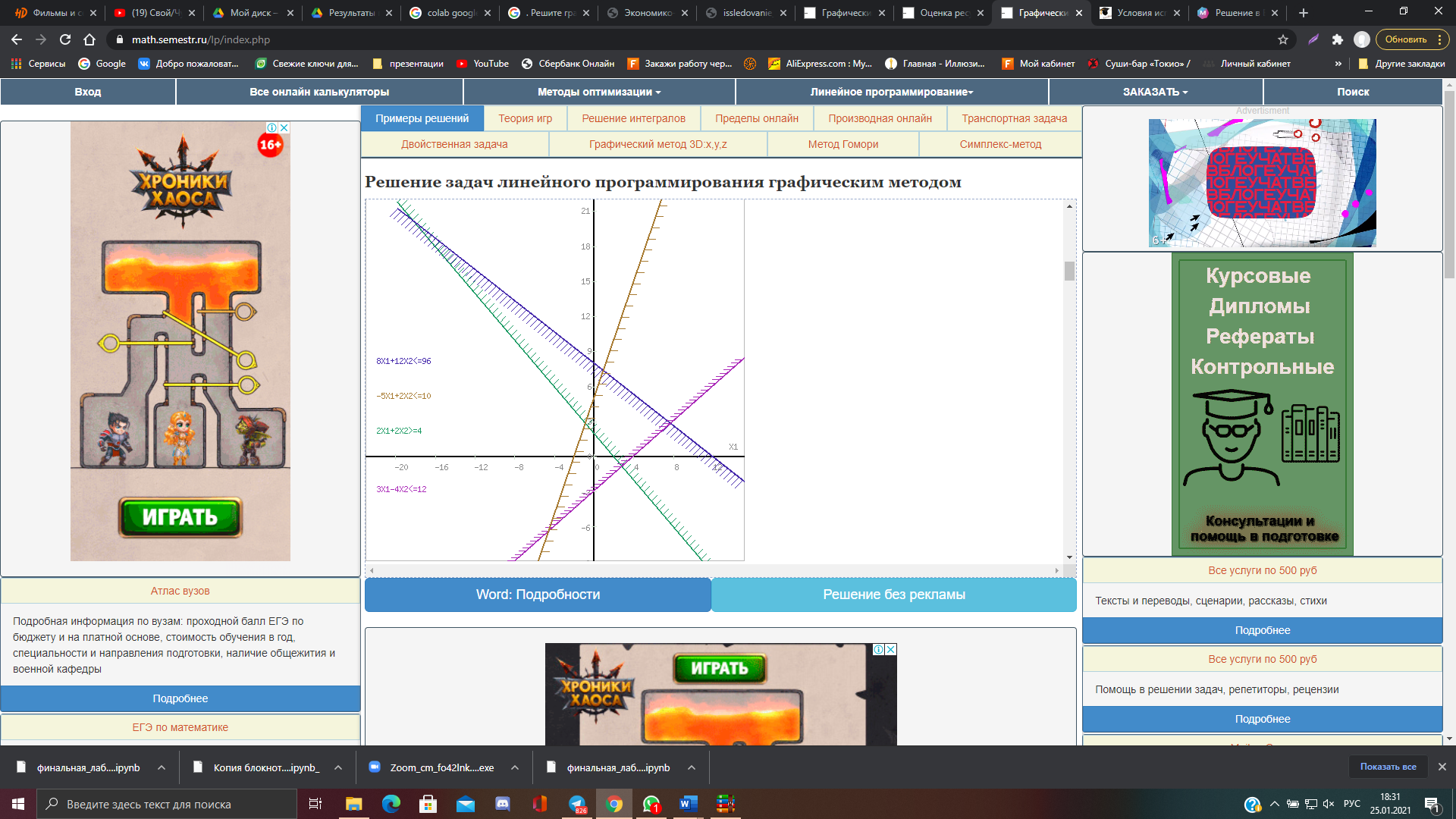 Шаг №2. Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений. 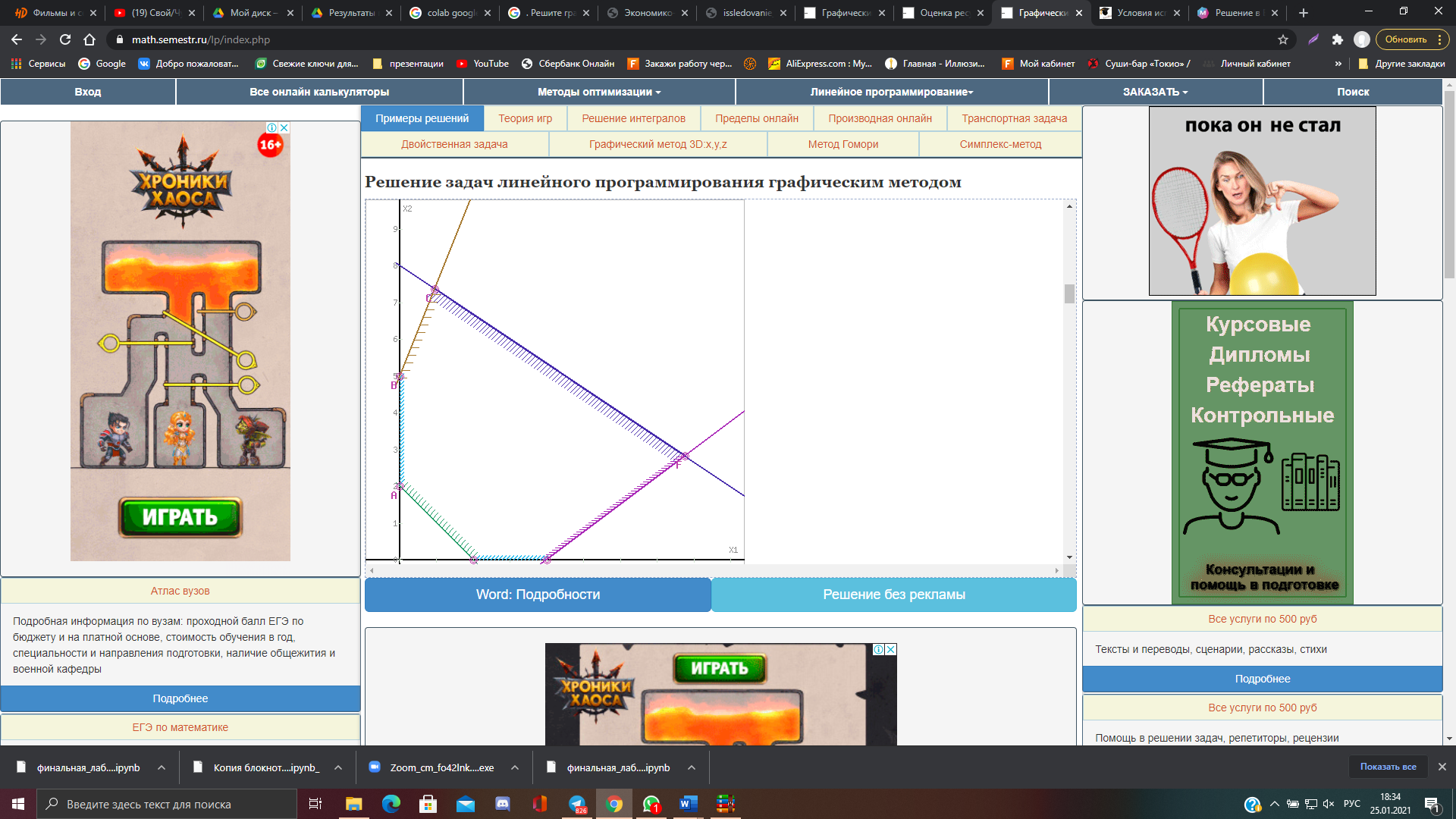 Шаг №3. Рассмотрим целевую функцию задачи F = 4x1+x2 → max. Построим прямую, отвечающую значению функции F = 4x1+x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (4;1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. 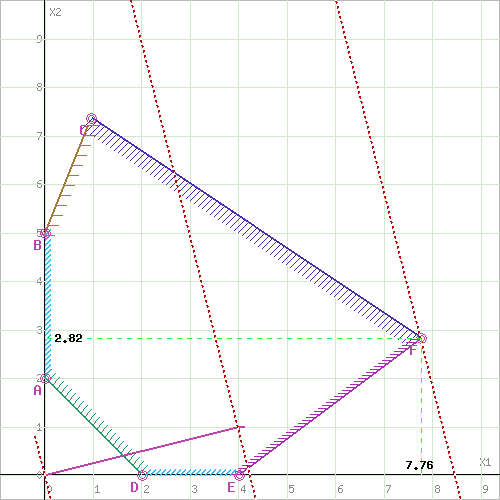 Прямая F(x) = const пересекает область в точке F. Так как точка F получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых: 8x1+12x2=96 3x1-4x2=12 Решив систему уравнений, получим: x1 = 7.7647, x2 = 2.8235 Откуда найдем максимальное значение целевой функции: F(X) = 4*7.7647 + 1*2.8235 = 33.8824 Изменение коэффициентов целевой функции. Изменение значений коэффициентов c1 и c2 приводит к изменению угла наклона прямой z. Существует интервалы изменения коэффициентов c1 и c2, когда текущее оптимальное решение сохраняется. Задача анализа чувствительности и состоит в получении такой информации. Необходимо определить интервал оптимальности для отношения c1 / c2 (или c2 и c1). Если значение отношения c1 / c2 не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным. Таким образом, в рамках анализа на чувствительность к изменениям коэффициентов целевой функции могут исследоваться вопросы: 1. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения. 2. На сколько следует изменить тот или иной коэффициент целевой функции, чтобы изменить статус некоторого ресурса. На предыдущем рисунке видно, что функция достигает своего оптимума в точке, которая является пересечением прямых (8x1+12x2=96) и (3x1-4x2=12). При изменении коэффициентов целевой функции эта точка останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона этих прямых. Алгебраически это можно записать следующим образом: при условии c1 ≠ 0 или при условии c2 ≠ 0 Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности. При c2 = 1 или -3/4 ≤ c1 ≤ 2/3 При c1 = 4 или -16/3 ≤ c2 ≤ 6 Оценка ресурсов. На данном этапе важно проанализировать следующие аспекты: 1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции. 2. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции. Оценка ресурса M2 Концевые точки отрезка определяют интервал осуществимости для ресурса M2. Количество сырья, соответствующего точке (4,0), равно 8·4 + 12·0 = 32 Таким образом, интервал осуществимости для ресурса M2 составляет ≤ M2 ≤ 32 Вычислим значение целевой функции в этих точках: F(4,0) = 4·4 + 1·0 = 16 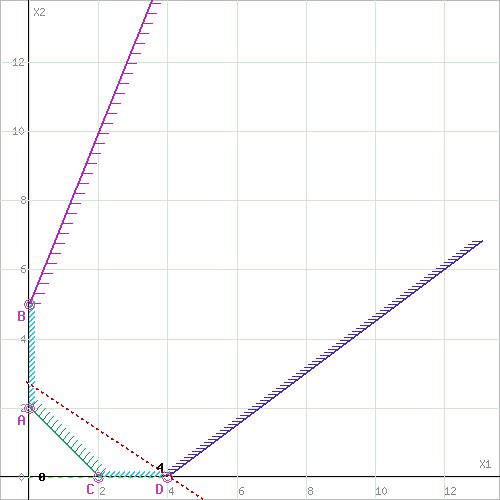 Изменение области решений при увеличении запасов ресурса M2 Оценка ресурса M3 Концевые точки отрезка определяют интервал осуществимости для ресурса M3. Количество сырья, соответствующего точке (0.947,7.368), равно 3·0.947 -4·7.368 = -26.632 Количество сырья, соответствующего точке (12,0), равно 3·12 + -4·0 = 36 Таким образом, интервал осуществимости для ресурса M3 составляет -26.632 ≤ M3 ≤ 36 Вычислим значение целевой функции в этих точках: F(0.947,7.368) = 4·0.947 + 1·7.368 = 11.158 F(12,0) = 4·12 + 1·0 = 48 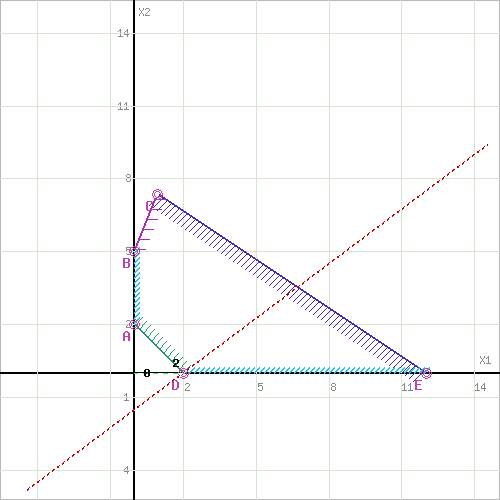 зменение области решений при увеличении запасов ресурса M3 Рассмотрим теперь вопрос об уменьшении правой части неактивного ограничения (1). Не изменяя оптимального решения, прямую L1 можно опустить до пересечения с оптимальной точкой. При этом правая часть ограничения (1) станет равной 2x1+2x2=21.176470588235, что позволит записать ограничение (1) в виде 2x1+2x2≥21.176470588235. Рассмотрим теперь вопрос об уменьшении правой части неактивного ограничения (4). Не изменяя оптимального решения, прямую L4 можно опустить до пересечения с оптимальной точкой. При этом правая часть ограничения (4) станет равной -5x1+2x2=-33.176470588235, что позволит записать ограничение (1) в виде -5x1+2x2≤-33.176470588235. yi определяет ценность каждой дополнительной единицы дефицитного ресурса. Чем больше значение yi, тем выше его приоритет при вложении дополнительных средств. Теория двойственности. Составим двойственную задачу к прямой задаче. -2y1+8y2+3y3-5y4≥4 -2y1+12y2-4y3+2y4≥1 -4y1+96y2+12y3+10y4 → min y1 ≤ 0 y2 ≥ 0 y3 ≥ 0 y4 ≥ 0 Отметим, что решение двойственной задачи дает оптимальную систему оценок ресурсов. Для решения двойственной задачи используем вторую теорему двойственности. Подставим оптимальный план прямой задачи в систему ограниченной математической модели: -2*7.76 -2*2.82 = -21.18 < -4 1-ое ограничение выполняется как строгое неравенство, т.е. ресурс 1-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y1 = 0 8*7.76 + 12*2.82 = 96 = 96 2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y2 > 0). 3*7.76 -4*2.82 = 12 = 12 3-ое ограничение прямой задачи выполняется как равенство. Это означает, что 3-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y3 > 0). -5*7.76 + 2*2.82 = -33.18 < 10 4-ое ограничение выполняется как строгое неравенство, т.е. ресурс 4-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y4 = 0 Поскольку x1>0, первое ограничение в двойственной задаче будет равенством. Поскольку x1>0, второе ограничение в двойственной задаче будет равенством. С учетом найденных оценок, новая система примет вид: y1 = 0, y4 = 0 -2y1+8y2+3y3-5y4 = 4 -2y1+12y2-4y3+2y4 = 1 96y2+12y3 → min или 8y2+3y3 = 4 12y2-4y3 = 1 96y2+12y3 → min Решая систему графическим способом, находим оптимальный план двойственной задачи:  Или 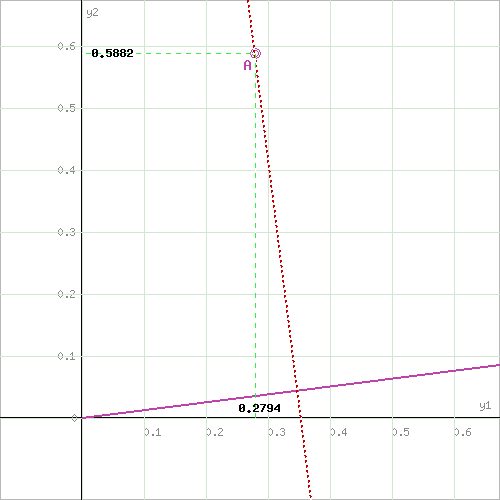 Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: 8y1+3y2=4 12y1-4y2=1 Решив систему уравнений, получим: y1 = 0.2794, y2 = 0.5882 Откуда найдем минимальное значение целевой функции: F(X) = 96*0.2794 + 12*0.5882 = 33.8824 y2 = 0.28 y3 = 0.59 Z(Y) = 96*0.28+12*0.59 = 33.88 Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов. Обоснование эффективности оптимального плана. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим: 1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что продукт №1 экономически выгодно производить, а его использование предусмотрено оптимальным планом прямой задачи (x1 > 0) 0*0 + 8*0.28 + 3*0.59 + 0*0 = 4 = 4 2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что продукт №2 экономически выгодно производить, а его использование предусмотрено оптимальным планом прямой задачи (x2 > 0) 0*0 + 12*0.28 + (-4)*0.59 + 0*0 = 1 = 1 Задача 2. Для изготовления продукции вида Pj 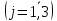 используется сырье трех видов Si используется сырье трех видов Si  , запасы которого ограничены и составляют соответственно bi , запасы которого ограничены и составляют соответственно bi  условных единиц. Расход сырья вида Si условных единиц. Расход сырья вида Si  на единицу готовой продукции Pj на единицу готовой продукции Pj 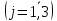 задан и равен aij. Доход от реализации единицы готовой продукции вида Pj составляет αj задан и равен aij. Доход от реализации единицы готовой продукции вида Pj составляет αj 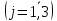 условных единиц. Построить математическую модель задачи, определяющую план производства продукции, обеспечивающий максимальную прибыль от реализации всей продукции. Решить ее симплексным методом. Составить двойственную задачу и найти ее решение по найденному оптимальному решению исходной задачи. условных единиц. Построить математическую модель задачи, определяющую план производства продукции, обеспечивающий максимальную прибыль от реализации всей продукции. Решить ее симплексным методом. Составить двойственную задачу и найти ее решение по найденному оптимальному решению исходной задачи.
В основе симплекс-метода лежит идея поиска базисного решения с последующим переходом от одного базиса к другому таким образом, чтобы целевая функция при этом все время увеличивалась, если речь идет о задаче максимизации. Для начала работы требуется, чтобы заданная система ограничений выражалась равенствами, причем в этой системе ограничений должны быть выделены базисные неизвестные. Решение задачи при помощи симплексметода распадается на ряд шагов. На каждом шаге от данного базиса Б переходят к другому, новому базису Б1 с таким расчетом, чтобы значение функции f(x) уменьшалось, т. е. fБ1≥fБ. Для перехода к новому базису из старого базиса удаляется одна из переменных и вместо нее вводится другая из числа свободных. После конечного числа шагов находится некоторый базис Б(k) , для которого fБ(k) есть искомый максимум для линейной функции f, а соответствующее базисное решение является оптимальным либо выясняется, что задача не имеет решения [7]. Переход от одного базисного решения к другому удобно осуществлять с помощью симплексных таблиц (табл. 1.4). Каждая такая таблица представляет базисное решение. В симплексной таблице введены следующие обозначения: Сбаз – коэффициенты при базисных переменных в целевой функции; хб – базисные переменные; b – свободные члены соответствующих ограничений; с1 … сn – коэффициенты при переменных в целевой функции; х1 … хn – переменные; а11 … аmn – коэффициенты при соответствующих переменных из системы ограничений; Zk - cn – индексная строка, каждый элемент которой получают расчетным путем. Zk определяют как сумму попарных произведений элементов первого столбца (Сбаз) и соответствующих элементов столбца при переменных; b/а – оценочные отношения, которые рассчитываются для определения ключевой строки путем отношения элементов столбца свободных членов (В) к соответствующим элементам ключевого столбца. 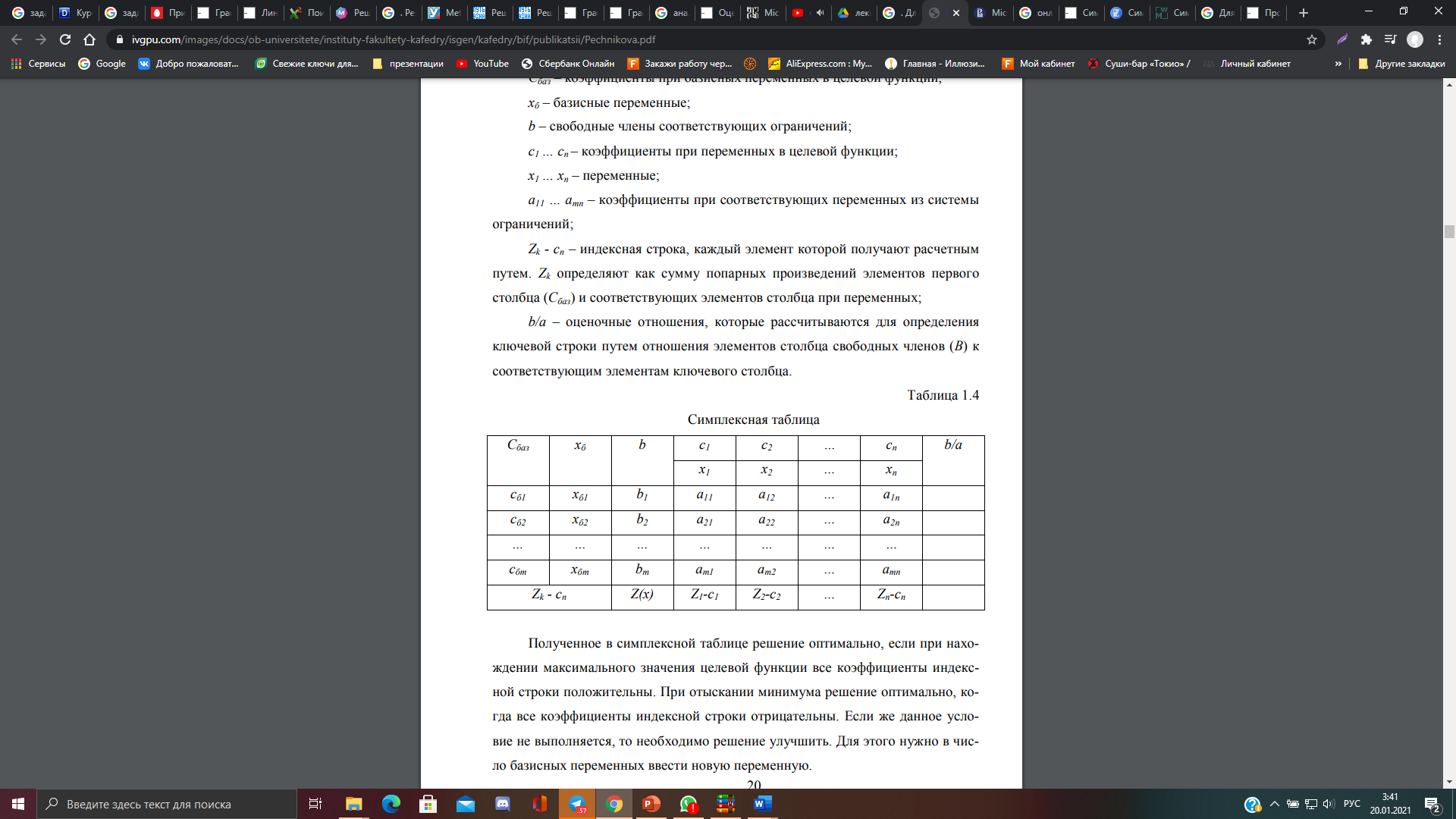 Полученное в симплексной таблице решение оптимально, если при нахождении максимального значения целевой функции все коэффициенты индексной строки положительны. При отыскании минимума решение оптимально, когда все коэффициенты индексной строки отрицательны. Если же данное условие не выполняется, то необходимо решение улучшить. Для этого нужно в число базисных переменных ввести новую переменную. Новая переменная, которая войдет в базисное решение, определяется следующим образом. В индексной строке отыскивается максимальное по абсолютной величине отрицательное число (при отыскании максимума целевой функции) или наибольшее положительное число (при отыскании минимума целевой функции). Соответствующий выбранному числу столбец симплексной таблицы называется ключевым. Далее следует установить, какую же из прежних базисных переменных заменит новая базисная переменная. С этой целью определяют ключевую строку. Ключевая строка отыскивается по отношению свободных членов к соответствующим положительным элементам ключевого столбца. Наименьшее отношение определяет ключевую строку. На пересечении ключевой строки и ключевого столбца расположен генеральный элемент. Для перехода от одной симплексной таблицы к другой существуют следующие правила: 1. Для нахождения элементов вводимой строки (соответствующей старой ключевой) необходимо все элементы ключевой строки поделить на генеральный элемент. 2. Элементы ключевого столбца, кроме находящегося в ключевой строке, переносятся в новую таблицу в виде нулей. 3. Те столбцы старой таблицы, у которых элемент в ключевой строке равен нулю, переносятся в новую таблицу без изменений. 4. Все остальные элементы новой таблицы находятся расчетным путем по следующей формуле:  где ан – новый элемент, ас – соответствующий старый элемент, ак.столб. – элемент ключевого столбца, ак.стр. – элемент ключевой строки, аг – генеральный элемент. Составленную новую симплексную таблицу проверяют, вычисляя индексную строку. Далее устанавливают, получено оптимальное решение или нет. Решение в симплексной таблице находится в столбце свободных членов: в индексной строке дано значение целевой функции, а все остальные элементы определяют значения базисных переменных. Для того чтобы решить задачу симплексным методом, необходимо выполнить следующее: 1. Привести задачу к каноническому виду. 2. Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решения ввиду несовместимости системы ограничений). 3. Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода. Если выполняется признак единственности оптимального решения, то решение задачи заканчивается. Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения. Рассмотрим решение задачи линейного программирования симплексным методом. https://ivgpu.com/images/docs/ob-universitete/instituty-fakultety-kafedry/isgen/kafedry/bif/publikatsii/Pechnikova.pdf РЕШЕНИЕ: Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6. Перепишем ограничения в каноническом виде: 3·x1 + 2·x2 + 3·x3 + x4 = 250 2·x1 + 3·x2 + x3 + x5 = 340 x1 + 2·x2 + 3·x3 + x6 = 220 Ищем начальное базисное решение: Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4 Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5 Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6 Начальная симплекс-таблица
Вычисляем дельты: Δi = C4·a1i + C5·a2i + C6·a3i - Ci Δ1 = C4·a11 + C5·a21 + C6·a31 - C1 = 0·3 + 0·2 + 0·1 - 7 = -7 Δ2 = C4·a12 + C5·a22 + C6·a32 - C2 = 0·2 + 0·3 + 0·2 - 8 = -8 Δ3 = C4·a13 + C5·a23 + C6·a33 - C3 = 0·3 + 0·1 + 0·3 - 5 = -5 Δ4 = C4·a14 + C5·a24 + C6·a34 - C4 = 0·1 + 0·0 + 0·0 - 0 = 0 Δ5 = C4·a15 + C5·a25 + C6·a35 - C5 = 0·0 + 0·1 + 0·0 - 0 = 0 Δ6 = C4·a16 + C5·a26 + C6·a36 - C6 = 0·0 + 0·0 + 0·1 - 0 = 0 Δb = C4·b1 + C5·b2 + C6·b3 - C7 = 0·250 + 0·340 + 0·220 - 0 = 0 Симплекс-таблица с дельтами
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -7 отрицательна. ( План оптимален, если в таблице отсутствуют отрицательные дельты.) Шаг 1 Определяем разрешающий столбец - столбец, в котором находится минимальная дельта: 2, Δ2: -8 Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения столбца 2 В найденном столбце ищем строку с наименьшим значением Q: Qmin = 110, строка 3. На пересечении найденных строки и столбца находится разрешающий элемент: 2 В качестве базисной переменной x6 берём x2.
Делим строку 3 на 2. Из строк 1, 2 вычитаем строку 3, умноженную на соответствующий элемент в столбце 2. Вычисляем новые дельты: Δi = C4·a1i + C5·a2i + C2·a3i - Ci Δ1 = C4·a11 + C5a21 + C2·a31 - C1 = 0·2 + 0 1/2+8·1/2- 7 = -3 Δ2 = C4·a12 + C5·a22 + C2·a32 - C2 = 0·0 + 0·0 + 8·1 - 8 = 0 Δ3 = C4·a13 + C5·a23 + C2·a33 - C3 = 0·0 + 0·(-7/2) + 8·3/2- 5 = 7 Δ4 = C4·a14 + C5·a24 + C2·a34 - C4 = 0·1 + 0·0 + 8·0 - 0 = 0 Δ5 = C4·a15 + C5·a25 + C2·a35 - C5 = 0·0 + 0·1 + 8·0 - 0 = 0 Δ6 = C4·a16 + C5·a26 + C2·a36 - C6 = 0·(-1) + 0·(-3/2) + 8·1 2 - 0 =4 Δb = C4·b1 + C5·b2 + C2·b3 - C7 = 0·30 + 0·10 + 8·110 - 0 = 880 Симплекс-таблица с обновлёнными дельтами
Текущий план X: [ 0, 110, 0, 30, 10, 0 ] Целевая функция F: 7·0 + 8·110 + 5·0 + 0·30 + 0·10 + 0·0 = 880 Проверяем план на оптимальность: план не оптимален, так как Δ1 = -3 отрицательна. Шаг 2 Определяем разрешающий столбец - столбец, в котором находится минимальная дельта: 1, Δ1: -3 Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения столбца 1 В найденном столбце ищем строку с наименьшим значением Q: Qmin = 15, строка 1. На пересечении найденных строки и столбца находится разрешающий элемент: 2 В качестве базисной переменной x4 берём x1.
Делим строку 1 на 2. Из строк 2, 3 вычитаем строку 1, умноженную на соответствующий элемент в столбце 1. Вычисляем новые дельты: Δi = C1·a1i + C5·a2i + C2·a3i - Ci Δ1 = C1·a11 + C5·a21 + C2·a31 - C1 = 7·1 + 0·0 + 8·0 - 7 = 0 Δ2 = C1·a12 + C5·a22 + C2·a32 - C2 = 7·0 + 0·0 + 8·1 - 8 = 0 Δ3 = C1·a13 + C5·a23 + C2·a33 - C3 = 7·0 + 0·(- 7/2) + 8·3/2 - 5 = 7 Δ4 = C1·a14 + C5·a24 + C2·a34 - C4 = 7·1/2 + 0·(- 1/4) + 8·(- 1/4) - 0 = 3/2 Δ5 = C1·a15 + C5·a25 + C2·a35 - C5 = 7·0 + 0·1 + 8·0 - 0 = 0 Δ6 = C1·a16 + C5·a26 + C2·a36 - C6 = 7·(- 1/2) + 0·(- 5/4) + 8·3/4 - 0 = 5/2 Δb = C1·b1 + C5·b2 + C2·b3 - C7 = 7·15 + 0·5/2 + 8·205/2 - 0 = 925 Симплекс-таблица с обновлёнными дельтами
Текущий план X: [ 15, 205/2, 0, 0, 5/2, 0 ] Целевая функция F: 7·15 + 8·205/2 + 5·0 + 0·0 + 0·5/2 + 0·0 = 925 Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален. Ответ: x1 = 15, x2 = 102,5, x3 = 0, F = 925 Задача 3. Решить задачу, используя алгоритм двойственного симплекс-метода   Задача 4. Для исходной задачи составить двойственную. Решить обе задачи симплексным методом или двойственным симплексным методом и по решению каждой из них найти решение другой. Одну из задач решить графическим методом. Провести анализ на чувствительность для задачи, решенной табличным симплекс-методом. 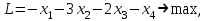 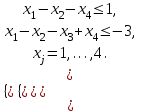 |
