Расчетное задание. Физика_Raschetnoe zadanie (вар-1). Решение Дано 32t t 3, рад t о 2 с r 0,1 м
 Скачать 107.5 Kb. Скачать 107.5 Kb.
|
|
Титульный лист ВАРИАНТ 1 Колесо радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается выражением =А+Bt+Ct3, где А=3 рад, В=2 рад/с, С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время 2 сек после начала движения: угловую скорость, линейную скорость, угловое ускорение, тангенциальное и нормальное ускорения. Решение: Дано: φ =3+2t+ t3, рад tо = 2 с R = 0,1 м Найти: ω(tо), V(tо), ε(tо), an(tо), aτ(tо) 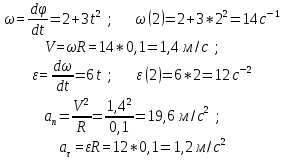 Ответ: Ответ: 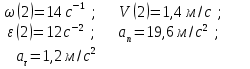 По ободу шкива, насаженного на общую ось с колесом, намотана нить, к концу которой подвешен груз массой 1 кг. На какое расстояние должен опуститься груз, чтобы колесо со шкивом получило скорость 60 рад/мин, если момент инерции колеса со шкивом 0,42 кг·м2, а радиус шкива 0,1 м? 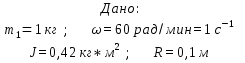 Решение: Сила, приложенная к системе, постоянная, следовательно, движение будет равноускоренным: 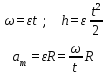 ← ← 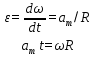 ; mg = a_m *m+ ε J /R; ; mg = a_m *m+ ε J /R; m g = m*ω R/t + (ω / t) J /R → t = ( m*ω *R + m J/R)/(m g) ; t = ( 1*1*0,1 +1*0,42/0,1)/9,81 = 0,438 c — за такое время угловая скорость шкива достигнет ω = 1 с-1. Ответ: груз опустится на 0,022 м = 22 мм Человек, бегущий со скоростью 8 км/ч, догоняет тележку массой 80 кг, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее. Масса человека 60 кг. С какой скоростью станет двигаться тележка? С какой скоростью стала бы двигаться тележка, если бы человек бежал навстречу тележке? 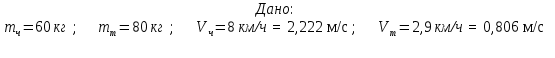 Найти: Vт+ч; Vт-ч Решение: По закону сохранения импульса, Vт+ч*( mт+ mч) = Vт * mт +Vч* mч →  Ответ: 5,08 км/час (1,41 м/с) и 1,77 км/час (0,49 м/с) Кислород массой 250 г, имеющий температуру 200 К, был адиабатически сжат. При этом была совершена работа 25 кДж. Найти конечную температуру газа. 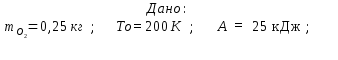 Найти Т1 Решение: Работа при адиабатическом сжатии (расширении) описывается формулой: А = CV (m/μ)*(T0- T1) → (T0- T1) = A/ (CV (m/μ) ) ; T1 = T0- A/ (CV (m/μ) ) = 200 -(-25000)/(20,95*(0,25/0,032) ) = 215.27 K Ответ: T1 = 215.27 K К источнику тока с ЭДС 1,5 В присоединили катушку с сопротивлением R=0,1 Ом. Амперметр показал силу тока, равную I1=0,5 А. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, сила тока I в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления r1 и r2 первого и второго источников тока. Решение: Составим систему уравнений: 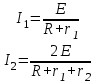 → → 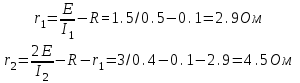 Ответ: П 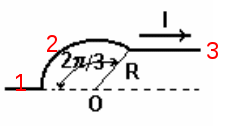 о бесконечно длинному проводу, изогнутому так, как показано на рисунке, течет ток I=200 А. Определить магнитную индукцию в точке О. Радиус дуги R=10 см. о бесконечно длинному проводу, изогнутому так, как показано на рисунке, течет ток I=200 А. Определить магнитную индукцию в точке О. Радиус дуги R=10 см.Решение: B_1 = 0 ; 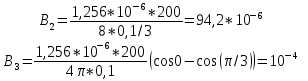 Ответ: Электрон, пройдя ускоряющую разность потенциалов U=400 В, попал в однородное магнитное поле с индукцией В=1,5 мТл. Определить: 1) радиус кривизны траектории; 2) частоту n вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции. Найти: R; n. Q/m =1,759×10^11 Кл/кг Решение: Из равенства сил FL = Q*V*B и Fц = m V2/ R → R = m V/ ( Q* B) Q*U = m V2/ 2 → Ответ: П 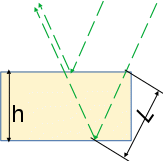 учок монохроматических (l=0,6 мкм) световых волн падает под углом 300 на находящуюся в воздухе мыльную пленку (n=1,3). При какой наименьшей толщине пленки отраженные световые волны будут максимально ослаблены интерференцией? максимально усилены? учок монохроматических (l=0,6 мкм) световых волн падает под углом 300 на находящуюся в воздухе мыльную пленку (n=1,3). При какой наименьшей толщине пленки отраженные световые волны будут максимально ослаблены интерференцией? максимально усилены?Решение: Отраженные световые волны будут максимально ослаблены интерференцией в том случае, когда 2L = λc/2; L = λc/4. L= h/cos 300 ; λc = λ /n → h= λ cos 300 /(4n) ; h= 0,6* cos 300 /(4*1,3) = 0.1 мкм — условие максимального ослабления. Для максимального усиления отраженные световыех волн условием будет 2L = λc; L = λc/2 → h= 0,6* cos 300 /(2*1,3) = 0.2 мкм Ответ: hmin= 0.1 мкм; 0.2 мкм Рентгеновское излучение (l=1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны lmax рентгеновского излучения в рассеянном пучке. Дано: =1 нм = 1 * 10-9 м Найти: λmax Решение: По формуле Комптона, длина волны после рассеяния λ“ равна λ“ = λ+2* λc* sin2 (φ/2), где λc = 2.43* 10-12 м. λmax = λ“ ( φ=180о) = λ+2* λc* 1 = 1 * 10-9 + 2*2.43* 10-12 = 1,005* 10-9 м Ответ: λmax = 1,005 нм |
