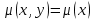Диффуры. Решение дифференциального уравнения
 Скачать 213.94 Kb. Скачать 213.94 Kb.
|
Определение: Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов): F(x, y(x), y’(x), y’’(x), … y(n)(x)) = 0 (1) т.е. уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала). Пример: y(4) – y + x = 0 - уравнение четвёртого порядка. Частным решением уравнения (1) на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция Общим решением (общим интегралом) уравнения (1) называется такое соотношение Ф(x, y, C1, C2, …Cn) = 0 (2) что: 1) Любое решение (2) 2) Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C1, C2, …, Cn.

Функция P(x, y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение: P(tx,ty)=tnP(x,y). Дифференциальное уравнение первого порядка y’=f(x, y) называется однородным, если правая часть удовлетворяет соотношению f(tx,ty)=f(x,y) для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y: f(tx,ty)=t0f(x,y)=f(x,y). Однородное дифференциальное уравнение можно также записать в виде: 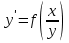 ; ;или через дифференциалы: P(x,y)dx+Q(x,y)dy=0, где P(x,y) и Q(x,y) − однородные функции одинакового порядка.
ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная y’(x) входят в уравнение в первой степени: 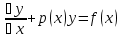 (1) (1)Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции: 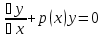 (2) (2)Неоднородное ДУ — ДУ, которое содержит не равный тождественно нулю свободный член имеет вид (1) Свойства решений: Св-ва решений ЛОДУ: 1) Пусть y(x) – решение ур-ния (2), тогда для любой постоянной С функция y1(x)=C*y(x) – также является решением ур-ния (2). 2)Пусть y1 и y2 - частные решения ур-ния (2), тогда линейная комбинация этих решений также является частным решением ур-ния (2):  , где , где  и и 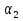 - постоянные - постоянныеСв-ва решений ЛНДУ: Структура общего решения ЛНДУ (ур-ние (1)) представлена в виде суммы общего решения ЛОДУ (2) и частного решения ЛНДУ (1), т.е. имеет следующий вид: yон = yoo + yчн , где yон – общее решение линейного неоднородного ДУ; yoo – общее решение линейного однородного ДУ yчн - частное решение линейного неоднородного ДУ Методы решений
Пусть дано ур-ние y’ + p(x)y = f(x) (1) Шаг 1 Решаем уравнение, обнулив правую часть y’ + p(x)y = 0 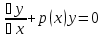 ; ;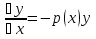 ; ; ; ;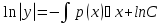 ; ;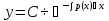 (3) (3)Шаг2 Константу С представляем в виде функции С(х), тогда (3) имеет вид: 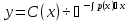 (4) (4)Подставим (4) в исходное ур-ние (1): 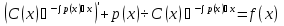 Получим 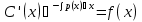 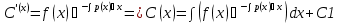 Вернем С(х) в ур-ние (4): 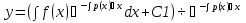 – общее решение ЛНДУ (уон), где – общее решение ЛНДУ (уон), гдеyоо = 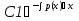 , ,yчн = 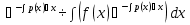
Решение ур-ния (1) ищется в виде: 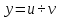 , где , где 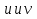 – неизвестные функции от х – неизвестные функции от х  , ,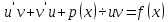 , ,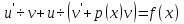 , ,Пусть выражение в скобке  = 0, тогда получаем систему: = 0, тогда получаем систему: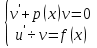  , ,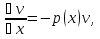  (*) (*)Пусть С = 1 (т.к. нужна только одна функция) Подставив (*) во 2 ур-ние системы, получим: 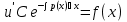  Таким образом, yон = 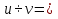 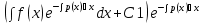 Уравнение Бернулли Уравнением Бернулли называется ДУ вида 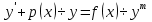 , где , где 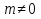 , , 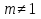 (при m = 0 уравнение линейно, при m = 1 - с разделяющимися переменными). (при m = 0 уравнение линейно, при m = 1 - с разделяющимися переменными).Решается следующим способом: производится замена 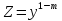 , ,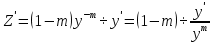  – ЛНДУ от функции Z, которое решается одним из вышеуказанных методов. – ЛНДУ от функции Z, которое решается одним из вышеуказанных методов.
Уравнением в полных дифференциалах называется ур-ние вида 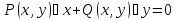 , ,(P(x, y), Q(x, y) - непрерывно дифференцируемы) в случае, если его левая часть является полным дифференциалом некоторой функции u(x, y), т.е. если существует такая функция u(x, y), что 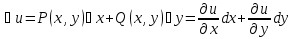 Условие для ур-ния в полных дифференциалах:  Для нахождения функции u(x, y) решается система уравнений 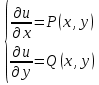 Из первого уравнения системы восстанавливаем функцию 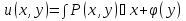 с точностью до произвольной дифференцируемой по y функции 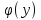 (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); затем из второго уравнения определяется (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); затем из второго уравнения определяется 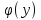 . . В случае, когда не выполняется условие  и ур-ние не является ур-нием в полных дифференциалах, то иногда можно подобрать интегрирующий множитель и ур-ние не является ур-нием в полных дифференциалах, то иногда можно подобрать интегрирующий множитель 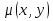 такой что, если на него домножить исходное ур-ние: такой что, если на него домножить исходное ур-ние: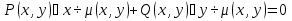 , то получится ур-ние в полных дифференциалах. , то получится ур-ние в полных дифференциалах.Нахождение интегрирующего множителя (два случая)
Найдем частную производную по у: 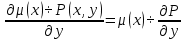 И по х: 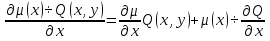 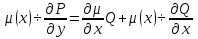 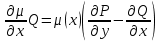 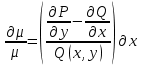 Т.к. 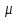 зависит от x, то и правая часть должна зависеть от х, обозначим ее как зависит от x, то и правая часть должна зависеть от х, обозначим ее как 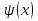  – ур-ние с разделяющимися переменными – ур-ние с разделяющимися переменнымиТ.к 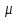 зависит только от x, то производная зависит только от x, то производная 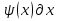 – обычная, а не частная. – обычная, а не частная.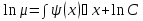 Таким образом,  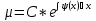
получим  
Уравнение вида F(x,y,y′)=0, где F − непрерывная функция, называется уравнением первого порядка, не разрешенным относительно производной. Если это уравнение можно решить относительно y′, то мы получаем одно или несколько явных дифференциальных уравнений вида y′=f(x,y), решаемое известными способами. В случае, когда уравнение невозможно привести к явной форме, чтобы его решить, используется метод введения параметра: 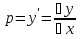 Допустим ур-ние разрешено относительно у. Введем замену 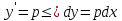 и получим и получим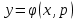 . .Найдем дифференциал левой и правой частей 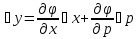 Т.к. 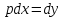 , то , то  – поучившееся ДУ решается одним из известных методов и находится – поучившееся ДУ решается одним из известных методов и находится  . .Полученный ответ записывается в виде 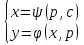 (по возможности следует исключить из системы переменную p). (по возможности следует исключить из системы переменную p).Уравнение Лагранжа Дифференциальное уравнение вида 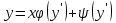 , где , где 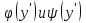 − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа. − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа. Полагая 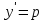 и дифференцируя по переменной x, получаем общее решение уравнения в параметрической форме: и дифференцируя по переменной x, получаем общее решение уравнения в параметрической форме: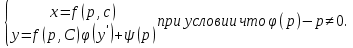 Уравнение Клеро Уравнение Клеро имеет вид:  , , где 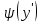 − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда 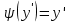 . Оно решается аналогичным образом с помощью введения параметра. Общее решение определяется выражением . Оно решается аналогичным образом с помощью введения параметра. Общее решение определяется выражением 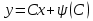 , в котором С – произвольная постоянная. , в котором С – произвольная постоянная.
Общее решение любого дифференциального уравнения первого порядка у' = f(х;у) содержит бесчисленное множество частных решений. Возникает естественный вопрос: как из этого множество частных решений выделить интересующее нас конкретное частное решение? Очевидно, требуется какое-то дополнительное условие. Если дифференциальное уравнение первого порядка у' = f(х;у) задано вместе с начальным для него условием 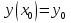 , то говорят, что для данного уравнения задана Задача Коши: , то говорят, что для данного уравнения задана Задача Коши: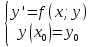 Решить её - это значит найти те частные решения дифференциального уравнения у' = f(х;у) , которые еще удовлетворяют и заданному начальному условию 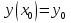 . .Теорема существования и единственности решения задачи Коши: 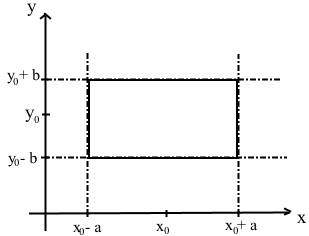 1) Пусть функция f(х,у) определена и непрерывна в некоторой области 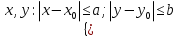 плоскости x0yи точка (x0; y0)принадлежит этой области. плоскости x0yи точка (x0; y0)принадлежит этой области.Тогда: существует решение задачи Коши, определенное на интервале (x0 − δ, x0 + δ) (где δ = min{a; b/m}, m = const). 2) Если в доб. к условию 1) частная производная fy(х,у) определена и непрерывна в той же области, то решение задачи Коши единственно в этом интервале (x0 − δ, x0 + δ).
Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y '(x), y ''(x), …, y(n)(x)) = 0 Метод решения уравнений, допускающих понижение порядка, состоит в том, что в исходном уравнении делается такая замена z(x) или p(y), относительно которой получается ур-ние более низкого порядка. 1 случай В уравнение не входит искомая функция y, т.е. уравнение имеет вид: F(x, y(k), y(k+1), . . . , y(n)) = 0. Тогда порядок уравнения можно понизить с помощью замены y(k) = z(x). 2 случай В уравнение не входит независимая переменная x, т.е. уравнение имеет вид F(y, y’, y’’, . . . , y(n)) = 0. Тогда порядок уравнения понижается с помощью замены y’ = p(y). 3 случай Уравнение однородно относительно y и его производных, т.е. F(x, ky, ky’, ky’’, . . . , ky(n)) = kmF(x, y, y’, y’’, . . . , y(n)). Тогда порядок ур-ния понижается подстановкой y’ = yz, где z – новая неизвестная функция. 4 случай Уравнение однородно относительно x и y в обобщенном смысле, т.е. F(kx, kmy, km−1y’, km−2y’’, . . . , km−ny(n)) = kmF(x, y, y’, y’’, . . . , y(n)). Для этого ур-ния делается замена x = et, y = zemt, где z = z(t) – новая неизвестная ф-ция, а t – новая независимая переменная. Данная замена приводит к уравнению, не содержащему независимую переменную t. Порядок такого уравнения понижается одним из ранее рассмотренных способов.
Функции f1(x), . . . , fn(x) называются линейно независимыми, если их линейная комбинация α1f1(x) + . . . + αnfn(x) = 0 только в случае, когда α1 = α2 = . . . = αn = 0. Функции f1(x), . . . , fn(x) называются линейно зависимыми, если существуют такие α1, α2 , . . .αn , не все равные нулю, что линейная комбинация α1f1(x) + . . . + αnfn(x) = 0. Пусть функции y1(x), y2(x), . . . , yn(x) имеют производные до (n − 1)-го порядка. Тогда определитель 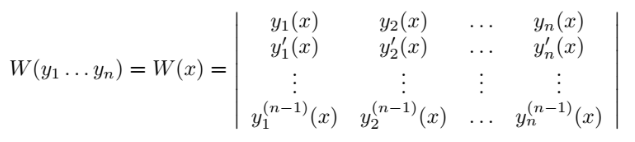 называется определителем Вронского. называется определителем Вронского.Теорема1 Если система функций линейно зависима, то их определитель Вронского равен нулю. Лемма1 Если y1(x), y2(x), . . . , yn(x) — линейно независимые решения уравнения Ly = 0, то определитель Вронского W(y1, . . . , yn) не обращается в нуль ни в одной точке области существования решений уравнения. (Если a1(x), . . . , an(x) ∈ (a, b), то W(y1, . . . , yn) не равн 0 ни при каком x0∈ (a, b)).
Формула Лиувилля устанавливает связь между вронскианом W(x), построенном на базе частных решений y1(x),y2(x),…yn(x) и коэффициентом a1(x) в дифференциальном уравнении. 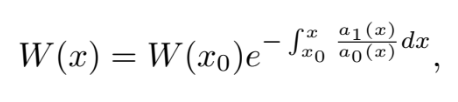 где a1(x) — коэффициент при y(n−1) в уравнении Ly = 0.
Система n линейно независимых решений линейного однородного дифференциального уравнения порядка n называется фундаментальной системой решений. Опред: Функции y1(x), . . . , yn(x) наз. линейно независимыми, если их линейная комбинация C1y1(x)+ . . . + Cnyn(x)= 0 тогда и только тогда, когда C1 = … Cn. Cистема n решений данного линейного однородного дифференциального уравнения порядка n является фундаментальной тогда и только тогда, когда ее определитель Вронского не равен нулю. Любое решение линейного однородного дифференциального уравнения порядка n есть линейная комбинация его фундаментальных решений. Линейное однородное дифференциальное уравнения порядка n не можетиметь более чем n линейно независимых частных решений. |