Решение для атома водорода
 Скачать 75 Kb.
|
|
Решение для атома водорода. Оператор Лапласа 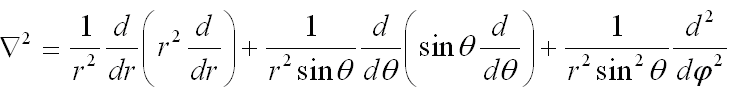 можно преобразовать к сферической системе координат, он будет иметь вид: С учетом всего вышеизложенного мы для атома водорода можем записать теперь уравнение Шредингера:  которое представляет собой дифференциальное уравнение второго порядка в частных производных. Уравнения такого типа решают обычно путем разделения переменных, т.е. волновую функцию  ищут в виде: , (2)где каждый из сомножителей зависит лишь от одной переменной. Для простоты вывода = R**. Подставим выражение для в общее уравнение: 1/r2* /r*(r2R/r) + 1/(r2sin)*/( sin*/)*R + +1/(r2sin2)*2/2)*R + (2 /r + 2E)R =0 Помножим обе части этого уравнения на 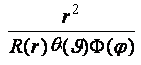 тогда получим /r*(r2 R /r)/R + 1/(sin)*/( sin*/)/ + +1/(sin2)*2/2)/ + r2*(2 /r + 2E) =0 /r*(r2 R/r)/R + r2*(2 /r + 2E) = 1/(sin)*/( sin*/)/ - 1/(sin2)*2/2)/ Легко убедится, что левая часть равенства зависит только от переменной r, а правая - от переменных и . Но части равенства, зависящие от разных переменных, будут, в общем случае, равны друг другу тогда и только тогда, когда левая и правая части равны некоторой константе c = l(l+1) Поэтому из общего уравнения получим два уравнения: /r*(r2 R/r)/R + r2*(2 /r + 2E) = с= l(l+1) (3)  домножим последнее уравнение на sin2 получим Левая и правая части равенства зависят от разных переменных  и  . И поэтому они должны быть равны константе. Положим, что эта константа положительна и равна m2, тогда можно получить два уравнения 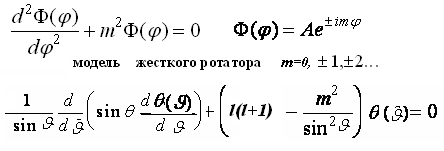 Из уравнения видно, что () =f(l,m). Тем самым мы исходное уравнение Шредингера (1), зависящее от трех переменных, свели к трем уравнениям. Будем теперь решать уравнение (3), зависящее от координаты  .После домножения на r2 уравнения для радиальной части получим  Решение этого уравнения также следует искать в виде ряда по степеням :Решение для радиальной части волновой функции  , которое с условием нормировки запишется как  где  - присоединенный полином Лягера, который в явном виде равен  И окончательно для нормированных радиальных составляющих волновой функции мы получим: R(r) = f(n,l).   Окончательно: R(r) = f(n,l), () =f(l,m), Ф() = f(m) или (r,,) = R(r)(n,l)*()(l,m)*Ф()(m) = f(n,l,m) |