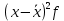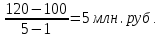СТАТИСТИКА. СТАТИСТИКА ЗАДАЧИ. Решение Для расчета используем формулу средней арифметической взвешенной где за значение признака примем середину интервала, рассчитанную
 Скачать 51.35 Kb. Скачать 51.35 Kb.
|
|
БЛОК 1 Рассчитайте среднюю величину и дисперсию.
Решение Для расчета используем формулу средней арифметической взвешенной где за значение признака примем середину интервала, рассчитанную  Для удобства расчетов составим вспомогательную таблицу.
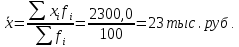 Дисперсия – средний квадрат отклонения индивидуальных значений признака от средней арифметической: 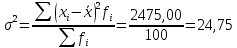 2.Рассчитайте моду.
Решение Мода: Мо = хо + i 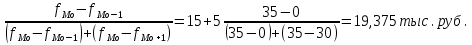 где х0 – нижняя граница модального интервала; i – величина интервала; fм0 – частота (плотность) модального интервала; f(м0-1) – частота интервала, предшествующего модальному; f(м0+1) – частота интервала, следующего за модальным. Модальный интервал – интервал с максимальной частотой, то есть интервал 15-20 тыс.руб 3. Рассчитайте медиану.
Решение Медиана: Ме = хо + i 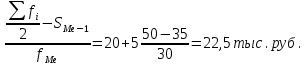 где Хmе – нижняя граница медианного интервала (медианный интервал – это интервал, на который приходится половина накопленных частот 100/2=50, на интервал 20-25 тыс.руб. приходится 35+30=65% накопленных частот); i – величина интервала; S(mе-1) – накопленная частота интервала, предшествующего медианному; 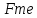 – частота медианного интервала. – частота медианного интервала.4. Рассчитайте первую квартиль.
Решение 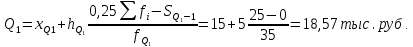 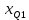 – нижняя границам квартильного интервала (квартильный интервал 15-20 тыс.руб., поскольку на него приходится 25% накопленных частот); – нижняя границам квартильного интервала (квартильный интервал 15-20 тыс.руб., поскольку на него приходится 25% накопленных частот);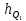 – величина квартильного интервала; – величина квартильного интервала;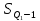 –сумма накопленных частот ряда, предшествующих квартильному интервалу; –сумма накопленных частот ряда, предшествующих квартильному интервалу;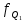 – частота квартильного интервала. – частота квартильного интервала.5. Рассчитайте третью квартиль.
Решение 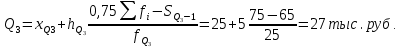 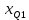 – нижняя границам квартильного интервала (квартильный интервал 25-30 тыс.руб., поскольку на него приходится 75% накопленных частот (30+35+25=90%)); – нижняя границам квартильного интервала (квартильный интервал 25-30 тыс.руб., поскольку на него приходится 75% накопленных частот (30+35+25=90%));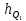 – величина квартильного интервала; – величина квартильного интервала;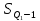 –сумма накопленных частот ряда, предшествующих квартильному интервалу; –сумма накопленных частот ряда, предшествующих квартильному интервалу;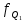 – частота квартильного интервала. – частота квартильного интервала.6. Рассчитайте первую дециль.
Решение Децилем называется структурная переменная, делящая распределение на 10 равных частей по числу единиц в совокупности. Децилей 9, а децильных групп 10. Децили определяются по формулам, аналогичным формуле для расчета медианы и квартилей. Децильный интервал для первого дециля придется на первый интервал (15-20 тыс.руб.) 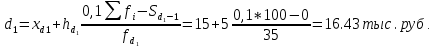 7.Рассчитайте девятую дециль.
Децилем называется структурная переменная, делящая распределение на 10 равных частей по числу единиц в совокупности. Децилей 9, а децильных групп 10. Децили определяются по формулам, аналогичным формуле для расчета медианы и квартилей. Децильный интервал для девятого дециля придется на интервал (25-30 тыс.руб.), поскольку на него приходится 90% накопленных частот (35+30+25=90%). 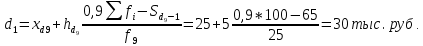 8. В интервале от 10 до 20 тыс. руб. находилась заработная плата 15 работников, в интервале от 20 до 40 тыс. руб. – 20 работников, в интервале от 40 до 60 тыс. руб. – 5 работников. Чему равна средняя заработная плата всех работников? Решение Для расчета используем формулу средней арифметической взвешенной где за значение признака примем середину интервала, рассчитанную  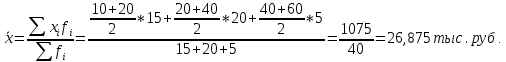 9. Средняя величина равна 100 рублей, а дисперсия средней величины – 225, чему равен коэффициент вариации? Решение Среднее квадратичное отклонение показывает, как колеблется основная масса единиц относительно средней арифметической: 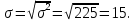 Коэффициент вариации используется для сравнительной характеристики и оценки степени однородности совокупности. 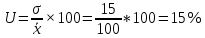 10. Коэффициент вариации составил 20%, а средняя величина – 33 руб. Чему равно среднее квадратическое отклонение? Решение Коэффициент вариации используется для сравнительной характеристики и оценки степени однородности совокупности. 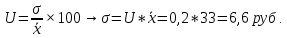 11. Коэффициент вариации составил 35%, а средняя величина – 70 руб. Чему равна дисперсия? Решение Дисперсия – средний квадрат отклонения индивидуальных значений признака от средней арифметической: 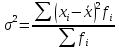 Среднее квадратичное отклонение показывает, как колеблется основная масса единиц относительно средней арифметической: 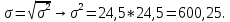 Коэффициент вариации используется для сравнительной характеристики и оценки степени однородности совокупности. 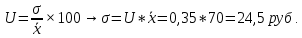 12. В интервале от 15 до 20 тыс. руб. находилась заработная плата 7 работников, в интервале от 20 до 45 тыс. руб. – 10 работников, в интервале от 45 до 65 тыс. руб. – 10 работников. Чему равна средняя заработная плата всех работников? Решение Для расчета используем формулу средней арифметической взвешенной где за значение признака примем середину интервала, рассчитанную  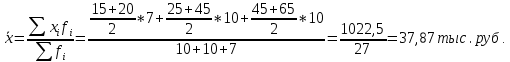 13. Модальный интервал в ряду распределения от 15 до 20 тыс. руб., доля численности населения, которая получает такой доход 30,4%, от 10 до 15 тыс. руб. получает 15,4% населения, а от 20 до 25 тыс. руб. – 10,4% населения. Рассчитайте точное значение модального дохода. Решение Мода: Мо = хо + i 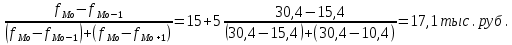 где х0 – нижняя граница модального интервала; i – величина интервала; fм0 – частота (плотность) модального интервала; f(м0-1) – частота интервала, предшествующего модальному; f(м0+1) – частота интервала, следующего за модальным. 14. До 25 тыс. руб. получает доход 40% населения, в интервале от 25 до 30 тыс. руб. доход получает 15% населения. Чему равна медиана? (Всего населения 100%) Решение Медиана: Ме = хо + i 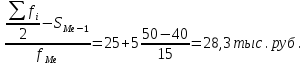 где Хmе – нижняя граница медианного интервала (медианный интервал – это интервал, на который приходится половина накопленных частот 100/2=50, на интервал 25-30 тыс.руб. приходится 40+15=55% накопленных частот); i – величина интервала; S(mе-1) – накопленная частота интервала, предшествующего медианному; 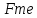 – частота медианного интервала. – частота медианного интервала.БЛОК 2 Чему равен цепной темп роста для 2019 г., если известно, что объем исследуемого показателя в 2019 г. =120 млн. руб., в 2018 г. = 100 млн. руб., в 2017 г. = 150 млн. руб. 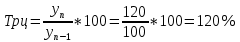 Чему равна базисный темп роста для 2019 г., если известно, что объем исследуемого показателя в 2019 г. =120 млн. руб., в 2018 г. = 100 млн. руб., в 2017 г. = 150 млн. руб. Решение: 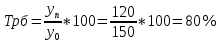 3. Временной ряд состоит из 5 уровней, уровень первого периода = 100 млн. руб., уровень последнего периода = 120 млн. руб., чему равен средний темп роста? Решение  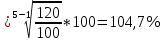 4. Временной ряд состоит из 5 уровней, уровень первого периода = 100 млн. руб., уровень последнего периода = 120 млн. руб., чему равен базисный абсолютный прирост последнего периода и среднегодовой абсолютный прирост? Решение
5. На 1 января товарные запасы оценивались в 300 тыс. руб., на 1 февраля – 320 тыс. руб., на 1 марта – 325 тыс. руб., на 1 апреля – 280 тыс. руб. Чему равен средний уровень товарных запасов в 1 квартале года? Решение Поскольку представленный ряд является моментным расчет проведем по формуле средней хронологической: 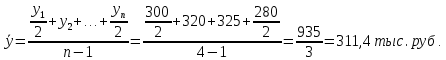 6. На 1 января численность населения города была 105,9 тыс. чел., на 1 марта – 105,7 тыс. чел., на 1 мая – 106,1 тыс. чел., на 1 июля– 106,4 тыс. чел. Чему равна средняя численность населения города? Поскольку представленный ряд является моментным расчет проведем по формуле средней хронологической. При этом представленные данные позволяют рассчитать среднюю численность населения за первое полугодие: 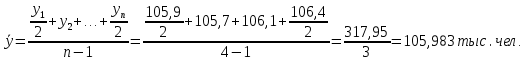 7. Коэффициенты роста к предыдущему году составили: в 2014 г. – 1,004 в 2015 г. -1,021, в 2016 г. – 1,033, в 2017 г. – 1,089. Чему равен базисный темп роста в 2017 г. (к 2013 г.)? Решение Произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста. 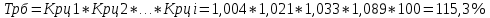 Базисный темп роста составляет 15,3%. 8. Коэффициенты роста к предыдущему году составили: в 2014 г. – 1,004 в 2015 г. -1,021, в 2016 г. – 1,033, в 2017 г. – 1,089. Чему равен средний темп роста в 2014-2017 гг.? Решение Средний темп роста равен: 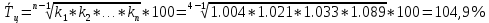 Средний темп роста за период составляет 104,9% 9. На 1 января товарные запасы оценивались в 250 тыс. руб., на 1 февраля – 275 тыс. руб., на 1 марта – 280 тыс. руб., на 1 апреля – 285 тыс. руб. Чему равен средний уровень товарных запасов в 1 квартале года? Решение Поскольку представленный ряд является моментным расчет проведем по формуле средней хронологической: 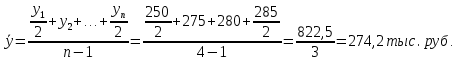 10. Темп роста показателя в 2020 г. По сравнению с 2015 г. Составил 155,3%. На сколько % в среднем ежегодно увеличивался показатель? Решение 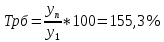  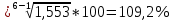 Среднегодовой прирост составил 9,2% 11. Темп роста показателя в 2018 г. По сравнению с 2015 г. Составил 88,7%. На сколько % в среднем уменьшался показатель ежегодно? Решение 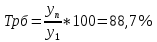  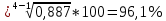 Среднегодовое сокращение показателя – 3,9%. 12. Цепные темпы роста составили в 2012 г. 105,6%, в 2013 г. 102,3%, в 2014 г. 98,8%. На сколько % вырос показатель за период 2011-2014 гг.? Решение Произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста. 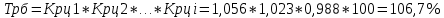 Базисный темп роста составляет 6,7%. 13. Цепные темпы роста составили в 2012 г. 105,6%, в 2013 г. 102,3%, в 2014 г. 98,8%. На сколько % в среднем ежегодно изменялся показатель за период 2011-2014 гг.? Решение Средний темп роста равен: 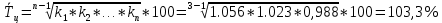 Средний темп прироста за период составляет 3,3% ежегодно 14. Абсолютное значение 1% прироста в 2015 г. составило 105,4 тыс. рублей, а абсолютный прирост показателя в 2015 г. был 200 тыс. руб. Чему равен цепной темп роста в 2015 г.? Решение Абсолютное значение 1% прироста 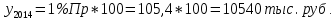 Абсолютный прирост составит: 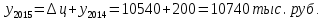 Цепной темп роста в 2015 году составит 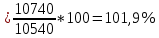 БЛОК 3 Оборот розничной торговли в мае составил 150 тыс. руб., в июне – 200 тыс. руб. Чему равен сводный индекс оборота товаров? Решение 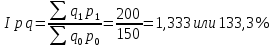 Оборот увеличился на 33,3% Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс цен? Решение Сводный индекс цен Пааше составит: 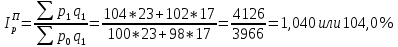 Цены в целом возросли на 4,0% Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс физического объема? Решение Сводный индекс физического объема Лайсперса составит: 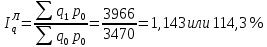 Совокупный объем продаж возрос на 14,3%. Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс оборота товаров? Решение Общий индекс товарооборота составит: 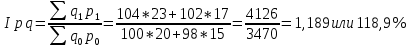 Товарооборот возрос на 18,9% Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Рассчитайте индивидуальные индексы цен? Решение Индивидуальный индекс цен рассчитывается по формуле: 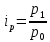 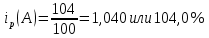 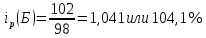 Цены товаров возросли на 4,0 и 4,1% соответственно. Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Рассчитайте индивидуальные индексы физического объема. Решение Индивидуальный индекс физического объема рассчитывается по формуле:  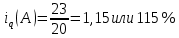 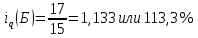 Физический объем продаж товаров возрос на 15,0 и 13,3% соответственно. Оборот товаров в базисном периоде составил 100 тыс. руб., затем тот же натуральный объем (физический объем товаров в базисном периоде) оценили в ценах отчетного периода – 135,4 тыс. руб. Как изменились цены на все товары в среднем в отчетном периоде по сравнению с базисным? Какой индекс цен можно посчитать с помощью этих данных? Решение Индекс цен по Лайсперсу рассчитывается по формуле: 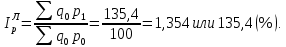 Цены на все товары возросли на 35,4% Если цены в отчетном периоде выросли на 3,4%, а индекс физического объема составил 98,3%. Чему равен индекс стоимости оборота товаров и услуг? Решение Названные индексы взаимосвязаны: 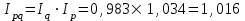 или 101,6%, то есть рост стоимости составил 1,6%. или 101,6%, то есть рост стоимости составил 1,6%.Цены на первый товар в отчетном периоде выросли на 3%, второй товар – 4%, а на третий цены снизились на 1%. Известно, что в базисном периоде оборот первого товара составил – 100 руб., второго – 150 руб., третий – 95 рублей. Чему равен общий индекс цен? Расчет проведем по формуле: 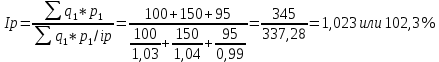 Общий рост цены составит 2,3% Цены на первый товар в отчетном периоде выросли на 3%, второй товар – 4%, а на третий цены снизились на 1%. Известно, что в отчетном периоде оборот первого товара составил – 100 руб., второго – 150 руб., третий – 95 рублей. Чему равен общий индекс цен? Расчет проведем по формуле: 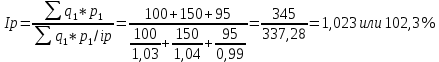 Общий рост цены составит 2,3% Выручка от реализации в отчетном периоде снизилась на 5,4%, а индекс цен составил 104,3%. Как изменился физический объем проданных товаров? Решение Названные индексы взаимосвязаны: 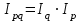 Откуда 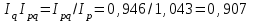 или 90,7% Снижение физического объема продаж составит 9,3% |