Решение для разных начальных условий с помощью ms excel. Начальные значения констант возьмем равными N031, P03, a0,1, b0,3, c0,01, d0,01
 Скачать 38.29 Kb. Скачать 38.29 Kb.
|
|
Практическая работа 2.2 Задание 1 Пусть N(t) – численность жертв (зайцев), P(t) – численность хищников в момент времени t (рысь). Тогда модель Лотки–Вольтерры имеет вид: 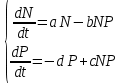 (1) (1)где а, b, c, d – положительные постоянные. Напомним, что система уравнений (1) основана на следующих допущениях: при отсутствии хищников жертвы размножаются неограниченно согласно уравнению 𝑑𝑁/𝑑𝑡 = 𝑎𝑁, которое называют иногда уравнением Мальтуса; хищники при отсутствии жертв вымирают согласно уравнению 𝑑𝑃/𝑑𝑡 = −𝑑𝑃; слагаемые, пропорциональные произведению NP, рассматриваются как превращение энергии одного источника в энергию другого (эффект влияния популяции хищников на популяцию жертв, то есть результат их встречи, состоит в уменьшении скорости прироста 𝑑𝑁/𝑑𝑡 численности жертв на величину NP, пропорциональную численности хищников). Теперь в этих уравнениях (1): N – численность популяции объектов охоты («жертв»); P – численность древних охотников («хищников») в рассматриваемом ареале; cNP – скорость рождения «хищников»; dP – смертность «хищников»; aN – скорость гибели «жертв» (считается, что их пищевая база неограниченна); bNP – скорость гибели «жертв» за счет их истребления «хищниками» (считается, что это единственная причина смертности «жертв»). Введем дополнительные обозначения: N0 – численность популяции зайцев (жертв), M 0 – численность популяции волков (хищников) в стартовый момент времени; Nt , Pt – численности популяций в t -й момент времени. Предполагается, что зайцы располагают неограниченным пространством и неограниченным количеством пищи, а также, что волки питаются зайцами. Два дифференциальных уравнения моделируют временную динамику численности двух биологических популяций жертвы N0 и хищника P0. Предполагается, что жертвы размножаются с постоянной скоростью a, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом b), и умирают естественным образом (смертность определяется константой d). В формуле для прироста численности зайцев появляется отрицательное слагаемое, учитывающее количество зайцев, ставших пищей для волков c. Рассчитаем решение для разных начальных условий с помощью MS Excel. Начальные значения констант возьмем равными N0=31, P0=3, a=0,1, b=0,3, c=0,01, d=0,01. Для начала введем начальные значения популяций для хищника и для жертвы, за тем в соответствии с системой уравнений введем формулы для каждой популяции. Количество шагов примем равным 140. В результате получаем следующую таблицу значений для каждой популяции в момент времени t:
Исходя из данных таблицы получаем следующий график: 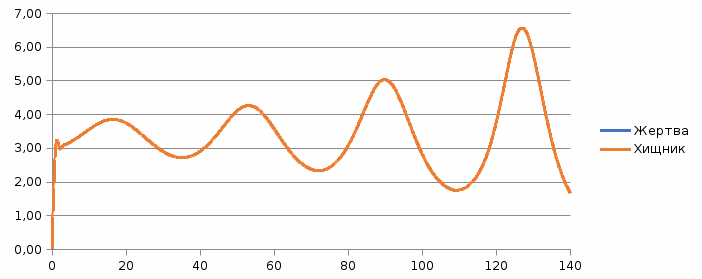 Из моделирования можно сделать следующие выводы: - Фазовые кривые системы уравнений Лотки-Вольтерра замкнуты. - Численность популяций хищников и жертв меняется периодически. - Период колебаний зависит от начальной численности популяций и коэффициентов системы . - Средняя численность популяции не зависит от начального значения, но зависит от коэффициентов системы. Задание 2 Для модели бесклассового сообщества характерна низкая плотность населения и общинная (родовая) организация человеческого сообщества. Человек полностью зависел от природы, шла постоянная борьба за выживание, а главным из добываемых ресурсов была пища. Человек был частью экосистемы и отличался от других стайных хищников, по-существу, лишь умением использовать для собственных нужд огонь и примитивные орудия труда. Изменение численности населения в конкретном ареале, в основном, определялось состоянием ресурсной базы и может быть описано моделью «хищник-жертва» - системой уравнений (1). Теперь в этих уравнениях: - N - численность популяции объектов охоты («жертв»); - P - численность древних охотников («хищников») в рассматриваемом ареале; - cNP - скорость рождения «хищников»; - dP - смертность «хищников»; - aN - скорость гибели «жертв» (считается, что их пищевая база неограниченна); - bNP - скорость гибели «жертв» за счет их истребления «хищниками» (считается, что это единственная причина смертности «жертв». Решения этих уравнений анализировались в 1 задании. Поскольку охотники-собиратели потребляли то, что было произведено в природе без их участия, численность популяции определялась внешними условиями, повлиять на которые они не могли. В модели численность охотников-собирателей колеблется около среднего значения P0 = a/b. Заметим, что именно этим объясняется относительная стабильность численности населения Земли на протяжении всего каменного века до эпохи неолита. Когда человек приручил животных и научился возделывать культурные растения, он превратился из охотника-собирателя в скотовода и земледельца. Таким образом, значительно увеличился коэффициент а и равновесная численность людей, поскольку величина коэффициента b, характеризующего потребление, осталась примерно на прежнем уровне. Задание 3 Простая модель борьбы двух противников называется моделью Ланчестера-Осипова. В модели Ланчестера-Осипова состояние системы описывается точкой (x, у) положительного квадранта плоскости. Координаты этой точки x и у - численности противостоящих армий. Уравнения модели имеют следующий вид: 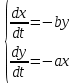 (4) (4)где а и b - мощность оружия армии x и армии у, соответственно. Другими словами, каждый солдат армии x убивает за единицу времени а солдат армии у (и соответственно каждый солдат армии у убивает b солдат армии x). Таким образом, общая эффективность всех выстрелов армии x дается как ax, а для армии у - как by. Предполагается, что непрерывная аппроксимация достаточно хороша, и скорость изменения численности войск пропорциональна эффективности выстрелов противной стороны. Жесткая модель (4) допускает точное решение в виде: 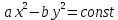 (5) (5)Изменение численности армий x и у происходит вдоль гиперболы, заданной уравнением (5). По какой именно гиперболе пойдет война, зависит от начальной точки. Гиперболы разделены прямой 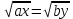 . Если начальная точка лежит выше этой прямой, то гипербола выходит на ось у. Это означает, что в ходе войны численность армии x уменьшается за конечное время до нуля - армия у выигрывает, противник уничтожен. Если же начальная точка лежит ниже прямой, то выигрывает армия х. На прямой же война заканчивается истреблением обеих армий. Но на это требуется бесконечно большое время: конфликт продолжает тлеть, когда оба противника уже обессилены. Из соотношения (5) следует, что на прямой . Если начальная точка лежит выше этой прямой, то гипербола выходит на ось у. Это означает, что в ходе войны численность армии x уменьшается за конечное время до нуля - армия у выигрывает, противник уничтожен. Если же начальная точка лежит ниже прямой, то выигрывает армия х. На прямой же война заканчивается истреблением обеих армий. Но на это требуется бесконечно большое время: конфликт продолжает тлеть, когда оба противника уже обессилены. Из соотношения (5) следует, что на прямой 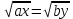 . Тогда первое уравнение системы (4) принимает вид: . Тогда первое уравнение системы (4) принимает вид: 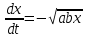 Его решением является: 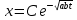 где С = const; x → 0 при t →∞. Из модели (4) следует вывод, что для борьбы с вдвое более многочисленным противником необходимо иметь в четыре раза более мощное оружие, с втрое более многочисленным - в девять раз и т.д. На это указывают квадратные корни в уравнении прямой. Ясно, что получившаяся жесткая модель сильно идеализирована, и её нельзя применять к реальной ситуации. В таком случае необходимо преобразовать систему к следующему виду: 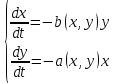 Эта система уравнений уже не решается в явном виде. Но модель за счет изменений a(x, у) и b(x, у) становится «мягкой». Кривые на плоскости (x, у) уже не гиперболы и разделяет их не прямая (рис. 6). Но основной качественный вывод остается прежним: ситуации «x выигрывает» и «у выигрывает» разделены нейтральной линией «обе армии уничтожают друг друга за бесконечное время». |
