Решение Для решения задачи используем интегральную формулу Муавра Лапласа
 Скачать 85 Kb.
|
|
2) Вероятность того, что пара обуви, наудачу из изготовленной партии, окажется 1-го сорта, равна 0,7. Определить вероятность того, что из 2100 пар, поступающих на контроль, число пар первосортной обуви окажется не менее 1000 и не более 1500. Решение: Для решения задачи используем интегральную формулу Муавра – Лапласа. Вероятность событий Рn (  ˂ m ˂  ) = Ф (х2) – Ф ( ) р = 0,7; 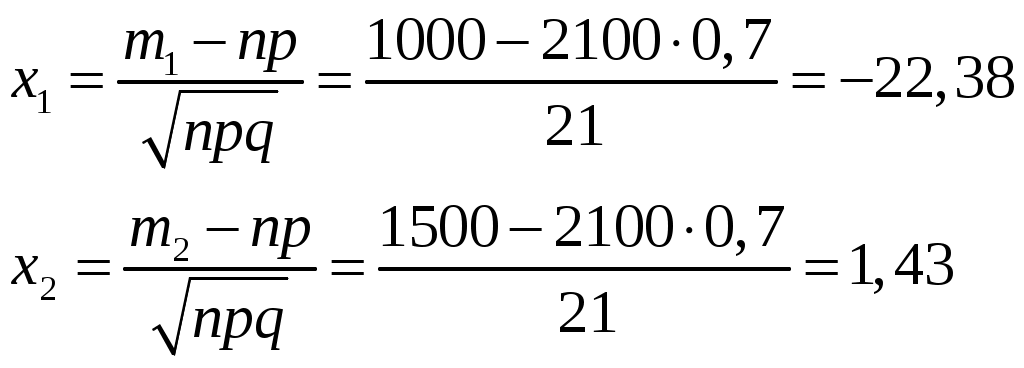n = 2100; = 1000; = 1500; q = 0,3 =21 Ф ( – х) = – Ф (х) , Ф (– 22,38) = – 0,5, Ф (1,43) = 0,4236 Ф (  ) – Ф ( ) = 0,5 + 0,4236 = 0,9236Ответ: Если число пар первосортной обуви окажется не менее 1000 и не более 1500, то из 2100 пар, поступающих на контроль, равна вероятности 0,9236. 1) В двух ящиках содержится по 20 деталей, из которых в первом ящике 16, а во втором 10 стандартных. Из первого ящика извлекается и перекладывается во второй ящик 2 детали. Определить вероятность того, что наудачу извлеченная после этого деталь из второго ящика будет стандартной. Решение. Испытание состоит в том, что наудачу выбирают из второго ящика деталь после перекладывания из 1-го ящика во второй 2 деталей. Пусть событие А - выбранный деталь – стандартная. Рассмотрим гипотезы: Событие Н1 – из 1 ящика во второй переложили 2 детали, среди которых 2 стандартных и ни одной нестандартной; Событие Н2 – из 1 ящика во второй переложили 2 детали, среди которых 1 белая и 1 чёрная; Событие Н3 – из 1 ящика во второй переложили 2 детали, среди которых 0 белых и 2 чёрных Так как события Н1, Н2 , Н3 образуют полную группу событий, и событие А может произойти с одним из этих событий, вероятность события А находим по формуле полной вероятности:  Определяем вероятности гипотез Н1, Н2 Н3 с помощью классического определения вероятности:  ,где: mi – число исходов, благоприятствующих появлению события Hi, n – общее число равновозможных исходов испытания. В 1 ящике находится 20 деталей, тогда общее число равновозможных исходов испытания равняется числу способов, которыми можно вынуть 2 детали из 20, то есть n =  Находим вероятность гипотезы Н1. 2 стандартные детали из 16 можно выбрать  способами, а 0 нестандартных из 4 -  =1 способом, тогда число исходов, благоприятствующих появлению события Н1, используя теорему умножения, будет равно:m =  Отсюда, вероятность события Н1 равна:  Аналогично находим вероятности гипотез Н2. Для события Н2 имеем: m2 =  Отсюда, вероятность события Н2 равна:  Для события Н3 имеем:   Контроль:  Находим условные вероятности события А при условии, что события Н1, Н2 ,  соответственно наступили, то есть вероятности с помощью классического определения вероятности: ,где: mi – число исходов, благоприятствующих появлению события А при условии, что событие Нi соответственно наступило; n – общее число равновозможных исходов испытания. При наступлении события Н1 во 2 ящике станет (10+2)=12 станд и 10 нестанд деталей, всего в урне 22 дет., тогда для события A | Н1 имеем: m1 = 12, a n = 22, отсюда  При наступлении события Н2 во 2 ящике станет (10+1)=11 станд. и (10+1)=11 нестанд, всего в урне 22 деталей, тогда для события A | Н2 имеем: m2 = 11, a n = 22, отсюда  Аналогично:  Таким образом, подставляя найденные вероятности в формулу полной вероятности, находим вероятность события А:  Ответ: Р(А) = 0,5273. |