Методы оптимизации. Решение Для учета изопериметрического ограничения введем дополнительную переменную состояния
 Скачать 313.54 Kb. Скачать 313.54 Kb.
|
|
Решение в матлабе для всех практик со скрином кода программы и с решением Практическая номер 3  Исходные данные: Уравнения движения: 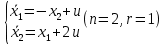 Граничные условия: 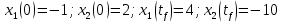 Критерий оптимальности в случае минимального времени равен: 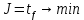 Решение: Для учета изопериметрического ограничения введем дополнительную переменную состояния: 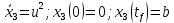 Таким образом, уравнения движения и граничные условия примут вид: 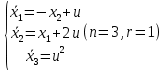 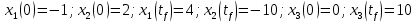 1) Гамильтониан 1) Гамильтониан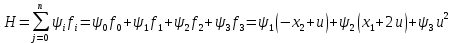 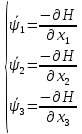 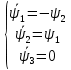 2) Условие стационарности 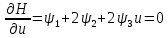 3) Из условия стационарности выразим 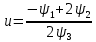 Подставив u в уравнения движения Эйлера-Лагранжа, получим систему уравнений: 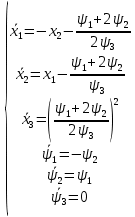 Решение данной системы дифференциальных уравнений с учетом граничных условий 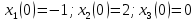 имеет вид: имеет вид: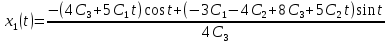 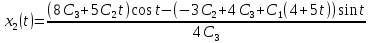 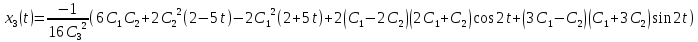 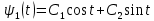 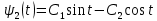 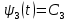 Управляющая переменная будет равна: 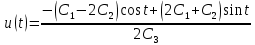 Применить граничные условия в конечный момент времени нельзя, так как неизвестно значение tf. Используя граничные условия в конечный момент времени 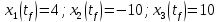 , запишем три уравнения , запишем три уравнения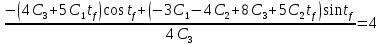 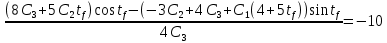 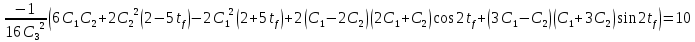 Так как конечное время не фиксировано, составим условие трансверсальности, обусловленное вариацией конечного времени: Так как конечное время не фиксировано, составим условие трансверсальности, обусловленное вариацией конечного времени: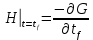 , где , где 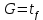 . .Таким образом: 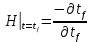 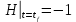 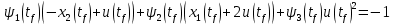 Подставив выражения 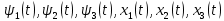 с заменой с заменой 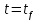 получим получим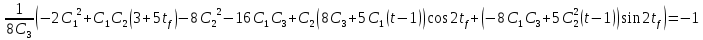 Запишем полученную систему из четырех уравнений (одно условие трансверсальности и три граничных условия) 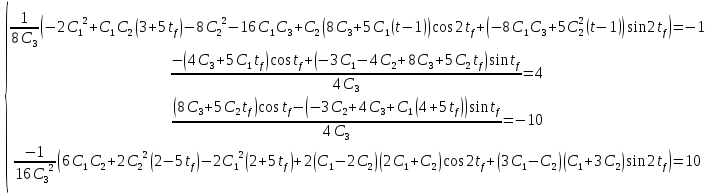 Практическая номер 4  Практическая номер 5  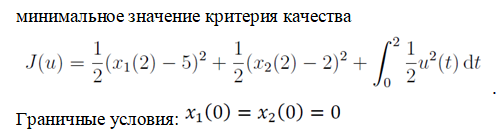 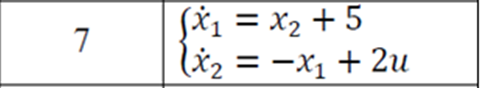 ------------------------------------------------------------------------------------------------------------------------------------------  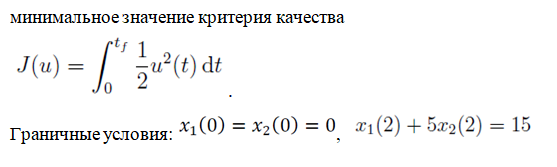 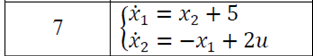 Практическая работа номер 7  |
