Контрольная по высшей математике. Контрольная работа_2_вариант5.docx. Решение Для вычисления данной частной производной, необходимо сначала продифференцировать функцию по y, затем 2 раза по z, а затем по x
 Скачать 281.22 Kb. Скачать 281.22 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ Кафедра высшей математики Контрольная работа по курсу ВЫСШАЯ МАТЕМАТИКА Вариант 5 Проверил: Выполнил: Ф.И.О. преподавателя Ст. гр. № __________ Ф.И.О.________________ Минск 2023 Задание1. Вычислить предел функции по правилу Лопиталя. 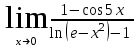 Решение Пусть функции f и g определены и непрерывны в некоторой окрестности  точки точки  за исключением, быть может, самой точки за исключением, быть может, самой точки  . Если существует предел . Если существует предел 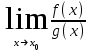 , то в целях устранения неопределенности , то в целях устранения неопределенности 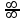 или или 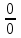 можно взять две производные – от числителя и знаменателя. При этом можно взять две производные – от числителя и знаменателя. При этом 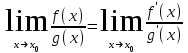 значение предела не изменится. Предел значение предела не изменится. Предел 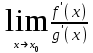 тоже должен существовать, в противном случае правило не применимо. тоже должен существовать, в противном случае правило не применимо.Подставим 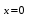 и получим неопределенность вида и получим неопределенность вида 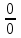 . .Найдем обе производные, от числителя и знаменателя. 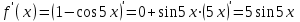 ; ;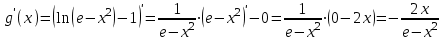 . .Применим правило Лопиталя и получим: 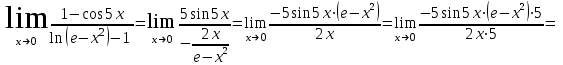 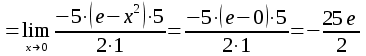 Ответ: 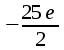 Задание2. Вычислить все частные производные второго порядка указанных функций. 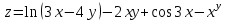 . .Решение Найдем частные производные первого порядка функции z: При нахождении 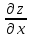 считаем аргумент y постоянным: считаем аргумент y постоянным: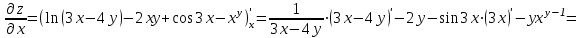 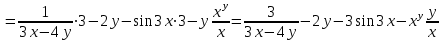 . .При нахождении 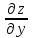 считаем аргумент x постоянным: считаем аргумент x постоянным: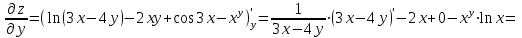 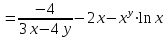 . .Найдем вторые и смешанную частную производную функции z: Для того, чтобы найти 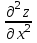 дифференцируем дифференцируем 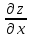 по x: по x: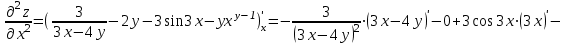 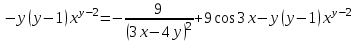 . .Для того, чтобы найти 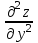 дифференцируем дифференцируем 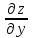 по y: по y: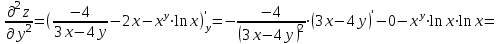 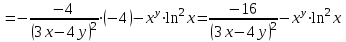 . .Для того, чтобы найти 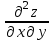 дифференцируем дифференцируем 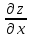 по у: по у: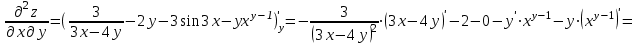 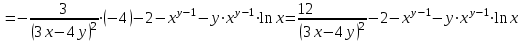 . .Ответ: 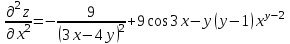 ; ;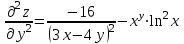 ; ;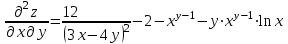 . .Задание3. Вычислить. 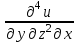 , если , если 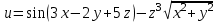 Решение Для вычисления данной частной производной, необходимо сначала продифференцировать функцию по y, затем 2 раза по z, а затем по x. При нахождении 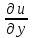 считаем аргументы z и x постоянными: считаем аргументы z и x постоянными: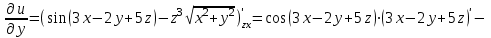 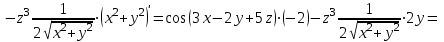 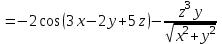 . .При нахождении 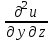 считаем аргументы y и x постоянными: считаем аргументы y и x постоянными: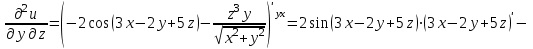 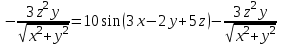 . .При нахождении 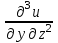 считаем аргументы y и x постоянными: считаем аргументы y и x постоянными: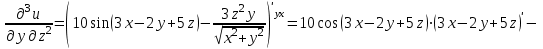 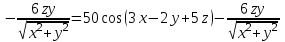 . .При нахождении 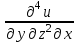 считаем аргументы y и z постоянными: считаем аргументы y и z постоянными: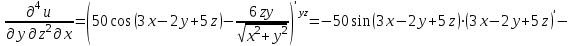 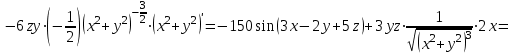 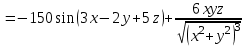 . .Ответ: 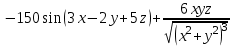 . .Задание4. Вычислить неопределенные интегралы: а) 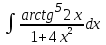 ; б) ; б) 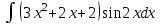 . .Решение а) 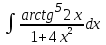 Выражение 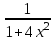 подведем под знак дифференциала, т.е.: подведем под знак дифференциала, т.е.: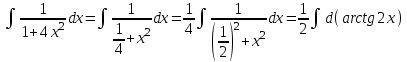 . .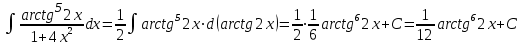 . .б) 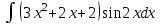 К данному интегралу применим метод интегрирования по частям: 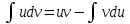 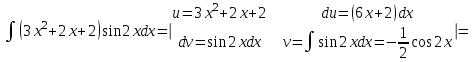 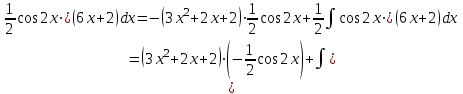 К полученному интегралу применим метод интегрирования по частям: К полученному интегралу применим метод интегрирования по частям: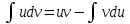 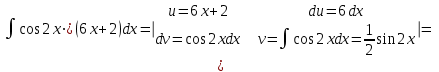 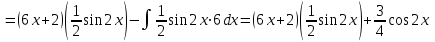 . .Получим: 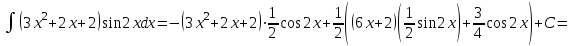 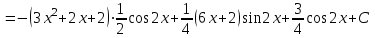 . .Ответ: а) 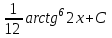 ; ;б) 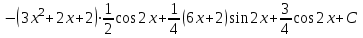 . .Задание5. Вычислить определенные интегралы: а) 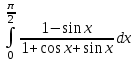 ; б) ; б) 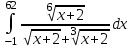 . .Решение а) Применяем универсальную тригонометрическую подстановку: 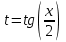 ; ; 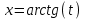 ; ; 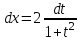 ; ; 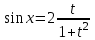 ; ; 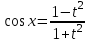 . .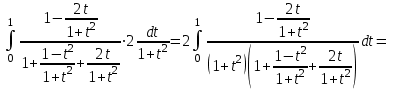 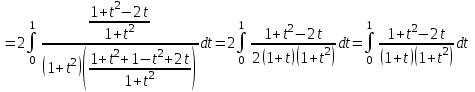 Используем метод разложения на простейшие. Разложим функцию на простейшие слагаемые: 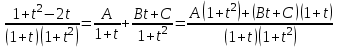 Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать: 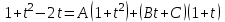 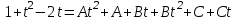 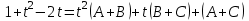 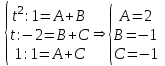 . .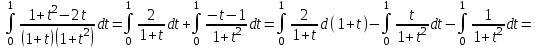 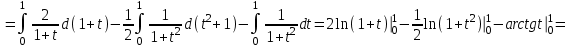 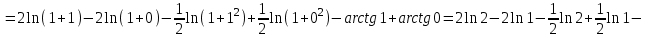 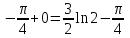 . .б) 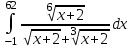 Введем замену: 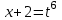 , тогда , тогда 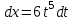 , , 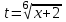 . .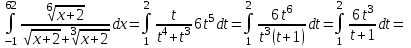 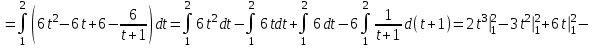 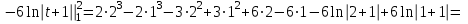 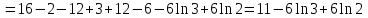 . .Ответ: а) 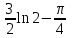 ; ;б) 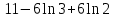 . .Задание6. Найти общее решение дифференциального уравнения: 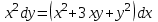 Решение 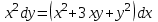 Сделаем замену: 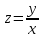 , , 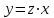 , , 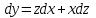 . .Получим: 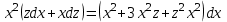 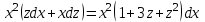 Первое решение x=0. Делим обе части на 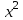 . .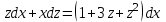 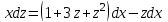 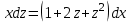 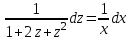 Проинтегрируем: 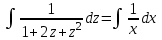 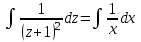 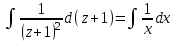 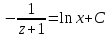 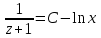 Учитывая, что 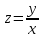 , получим: , получим: 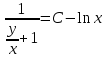 , ,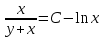 , ,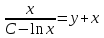 , ,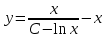 . .Ответ: 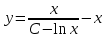 ; x=0. ; x=0.Задание7. Решить задачу Коши при начальном условии 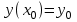 : :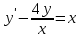 , , 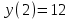 . .Решение Это линейное дифференциальное уравнение первого порядка относительно y, и оно имеет вид: 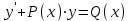 . .Решение будем искать в виде произведения двух функций 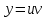 , где , где 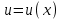 и и 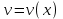 - неизвестные функции от переменной x. Тогда - неизвестные функции от переменной x. Тогда 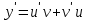 . Подставив y и . Подставив y и 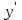 в исходное уравнение, получим: в исходное уравнение, получим: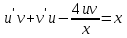 , ,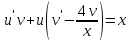 Функцию v найдем так, чтобы выражение в скобках равнялась нулю: 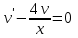 , ,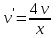 , ,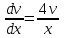 , ,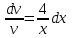 Получили уравнение с разделяющимися переменными. Проинтегрируем обе части и получим: 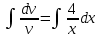 , ,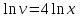 , ,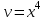 . .Подставим найденную функцию v в уравнение: 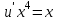 , ,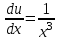 , ,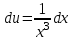 . .Проинтегрируем обе части и получим: 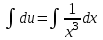 , ,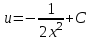 . .Тогда общее решение исходного дифференциального уравнения будет иметь вид: 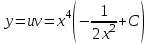 . .Найдем частное решение при условии: 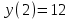 . .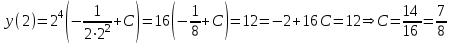 . .Таким образом, частное решение имеет вид: 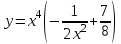 . .Ответ: 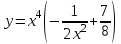 . .Задание8. Найти общее решение дифференциального уравнения. 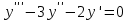 Решение Это линейное однородное дифференциальное уравнение третьего порядка с постоянными коэффициентами. Составим характеристическое уравнение и решим его. 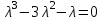 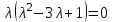 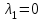 ; ; 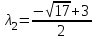 ; ; 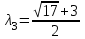 . .Получили 3 действительных корня. Общее решение однородного уравнения будет иметь вид: 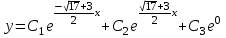 , ,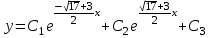 . .Ответ: 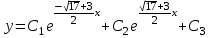 . .Задание9. Записать первые четыре члена ряда. Исследовать сходимость числовых рядов. 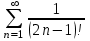 Решение Запишем первые четыре члена ряда: При n=1: 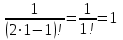 . .При n=2: 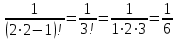 . .При n=3: 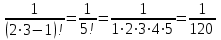 . .При n=4: 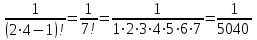 . .Вычислим интервал сходимости ряда с помощью признака Даламбера: 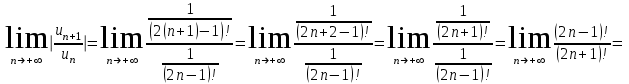 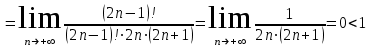 , значит, ряд сходится. , значит, ряд сходится.Ответ: сходится. Задание10. Найти радиус и область сходимости степенного ряда. 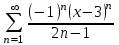 Решение Вычислим интервал сходимости ряда с помощью признака Даламбера: 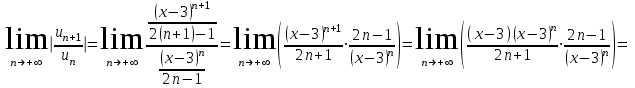 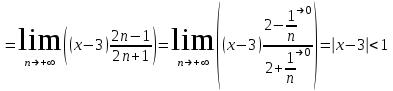 . .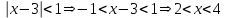 . .Радиус сходимости: 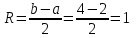 . .Исследуем сходимость на концах интервала. При x=2: 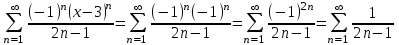 . . Рассмотрим два положительных числовых ряда 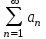 и и 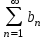 . Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу: . Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу: 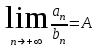 , то оба ряда сходятся или расходятся одновременно. , то оба ряда сходятся или расходятся одновременно.Возьмем расходящийся ряд 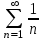 . .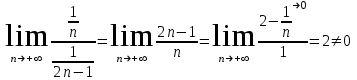 , значит, ряд , значит, ряд 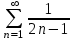 тоже расходится. тоже расходится.При x=4: 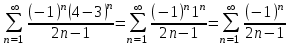 . .Рассмотрим первые три члена ряда: 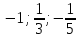 . .Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется: 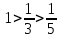 . .б) По второму признаку Лейбница предел ряда должен стремится к 0. 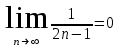 . .Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится. Но, т.к. 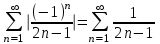 расходящийся ряд, то в данной точке ряд сходится условно. расходящийся ряд, то в данной точке ряд сходится условно.Область сходимости степенного ряда 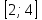 . .Ответ: 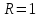 , область сходимости степенного ряда , область сходимости степенного ряда 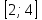 . . |
