Теорвер. Теория вероятности. Решение Доля деталей, произведенных на каждом заводе, от общего объема 1 30% 0,3 2 1 0,3 0,7
 Скачать 15.79 Kb. Скачать 15.79 Kb.
|
|
186(1) На склад поступают однотипные детали с двух заводов – №1 и №2. Завод №1 поставляет 30% деталей, из которых 10% имеют низкое качество. Завод №2 производит детали, из которых 80% имеют высокое качество. Найти вероятность того, что наугад взятая со склада деталь будет высокого качества. Решение: Доля деталей, произведенных на каждом заводе, от общего объема: №1: 30% = 0,3 №2: 1 – 0,3 = 0,7 Вероятности того, что изделие с заводов №1 и №2 будут высокого качества равны: 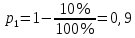 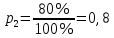 Вероятность того, что наугад взятая со склада деталь будет высокого качества: 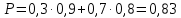 186(2) Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего равна 0,3; второй – 0,6; третий – 0,4 и четвертый – 0,25. Найти вероятности того, что в течение смены хотя бы один станок не потребует внимания мастера. Решение: Вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера (не все станки потребуют внимания): 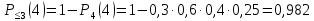 216(1) n = 900; p = 0,6. Определить вероятность того, что в 900 опытах событие произойдёт от 600 до 800 раз. Решение: q = 1 – p = 1 – 0,6 = 0,4 Используем интегральную теорему Лапласа: 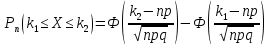 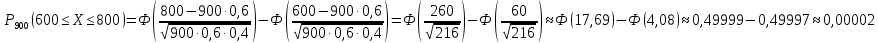 216(2) n = 800; p = 0,6. Определить вероятность того, что в 800 опытах относительная частота появления события А отклонится от вероятности р=0,6 не более чем на 0,05. Решение: q = 1 – p = 1 – 0,6 = 0,4 Используем следующую формулу: 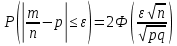 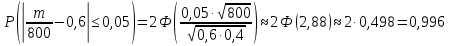 216(3) Бензоколонка заправляет легковые и грузовые автомобили. Вероятность того, что проезжающий легковой автомобиль заедет на заправку, равна 0,3. Оценить границы, в которых с вероятностью не меньше 0,79 находится доля заправившихся в течение суток легковых автомобилей, если за это время всего заправилось 100 автомобилей. Решение: q = 1 – p = 1 – 0,3 = 0,7 Используем следующую формулу: 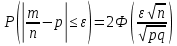 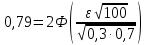  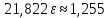  Тогда доля заправившихся в течение суток легковых автомобилей заключена в границах: 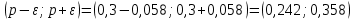 186(3) Среди 8 лотерейных билетов имеется 2 билета с выигрышем. Наудачу покупают три билета. Найти вероятность покупки одного выигрышного билета. Решение: Общее число исходов – количество способов выбора 3 билетов из 8: 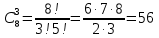 Благоприятствующие исходы – количество способов выбора 1 выигрышного билета из 2 билетов с выигрышем, а оставшиеся 2 билета должны быть выбраны из 6 невыигрышных: 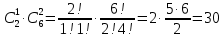 Вероятность покупки одного выигрышного билета равна отношению числа благоприятствующих событию исходов к общему числу исходов. 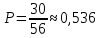 |
