открытый урок. Решение дробных рациональных уравнений. Цели
 Скачать 83.95 Kb.
|
|
Тема урока. Решение дробных рациональных уравнений. Цели: Образовательная: закрепление знаний и умений по решению дробных рациональных уравнений. Развивающая: развитие мыслительной деятельности. Воспитательная: воспитание самостоятельности и трудолюбия. Тип урока. Урок закрепления полученных знаний. Оборудование. Демонстрационные таблички, листы с заданиями, инструкциями к выполнению заданий и оцениванию результатов. 1.Организационный момент. Здравствуйте, ребята. Сегодня урок проведу у вас я. У нас сегодня присутствуют гости на уроке. Надеюсь, что это не повредит нашей работе, а наоборот поможет проявить наши лучшие качества. - Сегодня наше учебное занятие мы начнем с минутки доброты. Подумайте о чем-нибудь хорошем, ведь миром правит доброта и любовь. - Подумали? - И пусть это состояние останется до конца урока. Эпиграфом к уроку будут слова известного ученого Михаила Васильевича Ломоносоа. «Математику уже затем учить надо, что она ум в порядок приводит» А чтобы узнать чем мы сегодня будем заниматься на уроке, я предлагаю вам разгадать ребус. (Решение, уравнение). Ученики: Решать уравнения. Учитель: Что же мы будем делать на уроке? (Решать уравнения). (дробно рациональные) Тема нашего урока решение дробных рациональных уравнений. Так как вы уже умеете решать уравнения такого типа, то целью урока будет являться обобщение и систематизация знаний по данной теме. 2.Актуализация знаний Ответьте на вопросы: Какие уравнения называются рациональными уравнениями?( Уравнения называются рациональными, если его левая и правая части являются рациональными выражениями) Какие рациональные уравнения называются дробными?( Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называют дробным.) Назовите алгоритм решения дробных рациональных уравнений? Сколько корней имеют уравнения? Можете ли вы не решая его дать мне ответ? К этому вопросу вернемся чуть позже. Алгоритм решения дробных рациональных уравнений: 1.Определить допустимые значения (т.е. значения переменной, которые не обращают знаменатель в нуль, т.к. делить на нуль нельзя). 2. Найти общий знаменатель дробей. 3.Умножить обе части уравнения на общий знаменатель. 4. Решить полученное целое уравнение. 5. Исключить из его корней те, которые обращают в нуль общий знаменатель. 6. Записать ответ. Учитель: А теперь давайте вспомним какие типы уравнений вы уже умеете решать? 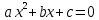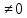(линейное ax+b=c (a,b,c некоторые числа, x-переменная) , квадратное(  где a,b,c –некоторые числа, x-переменная, a , дробно-рациональное)Задание 1. Определите тип уравнений. 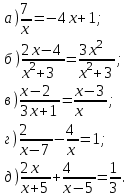 Учитель: Вы сказали, что один из пунктов алгоритма решения дробно-рационального уравнения является нахождение общего знаменателя. Я вам предлагаю найти общий знаменатель в уравнениях. (слайд ) 4.Закрепление изученного материала. Сейчас мы поработаем в парах. Работая в парах, вы можете помогать друг другу, но результаты записывайте каждый свои . В начале листа напишите свои фамилии, определите, кто в паре будет под №1, а кто под №2. При оценивании результаты пишите под своим номером. Успех на соревнованиях начинается со старта. Чтобы успешно решить дробное рациональное уравнение, с чего надо начать? (с нахождения ОДЗ). Найдите ОДЗ. Итак, мы начинаем. По таблице и своим решениям составьте высказывание одного известного учёного о трудолюбии. Прочитать вслух высказывание.
7 1 2 5 4 6 3 После отгадывания вывесить на доске высказывание. «Нет без явно усиленного трудолюбия ни талантов, ни гениев». Д.И. Менделеев. Физкультминутка. Во время физминутки дается задание последовательно перемещать взгляд с одной фигуры на другую (самостоятельно) или по названию фигуры (цвета) учителем. Упражнение можно выполнять сидя и стоя.  Упражнения: «8», «знак бесконечности», «геометрическая зарядка». Цель: снятие зрительного напряжения. Задание 1: нарисуйте движениями глаз на доске цифру 8. Задание 2: нарисуйте движениями глаз на доске знак бесконечности ∞. А теперь вернемся к вопросу о количестве корней. Уравнения также можно решить графическим способом. Отдельно построить график функции слева и справа и найти точки пересечения. Этим мы сейчас и займемся. С помощью программы «Граф» постройте графики функции, ответьте на вопрос сколько точек пересечения имеют графики и найдите чему равен x. 5.д/з Я предлагаю вам побывать в роли учителя математики и откорректировать предложенные вам решения уравнений, причем задание у всех разное. №611 (решить графически и с помощью алгоритма)
Рефлексия.(отметить на листе) 1. Я на уроке работал(а) (с желанием, без желания) 2. Я всё делал(а) сам (помогали) 3. Мне на уроке было интересно (скучно) 4. Моя оценка за урок Урок сегодня завершен, Но каждый должен знать: Познание, упорство, труд Всегда к успеху приведут! Самостоятельная работа. Учащимся предлагается дифференцированная самостоятельная работа, трех уровней сложности: А – обязательный минимум знаний по этой теме, В – упражнения среднего уровня сложности, С – упражнения высокого уровня сложности, Д – упражнения повышенной степени сложности. Для получения оценки «3» - необходимо выполнить 2 уравнения уровня А, на оценку «4» - необходимо решить 2 уравнения уровня В, на оценку «5» - допускается решение двух уравнений уровня С или одного уравнения уровня В и одного уравнения уровня С, а также возможность решения одного уравнения уровня Д. Каждый учащийся, оценивая свои возможности выбирает приемлемый для себя уровень. Уровень А 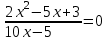 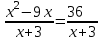 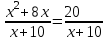 Уровень В     Уровень С    Уровень Д   7. Домашнее задание. Подведение итогов. Выставление оценок. Подведение итогов урока. Домашнее задание: Выбрать и решить два уравнения из предложенных
Решить уравнения в тетради. Сверить с ответами на доске. В графе «оценивание» каждый под своим номером записывает результаты: против правильно решённого уравнения ставите 1б, против неправильно решённого уравнения ставите прочерк - По просьбе учителя рассказываете решение каждого уравнения ( по желанию). Если ответ правильный, ставите 1б в графе «За ответ». Подведите итог (сколько всего баллов)
Инструкция к выполнению. 1. Определите ОДЗ в каждом уравнении и запишите в тетрадь как показано в таблице. 2. Запишите против каждого х 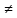 результат.3. Сверьте с ответами на доске. 4. Графу «оценивание» заполняете, как в первой таблице. 5. Пользуясь таблицей ниже и нумерацией перед х 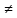, составьте высказывание известного учёного о трудолюбии. 1б, если верноВысказывание____________________ ________________________________ Подведите итог.
1.Решите дробное рациональное уравнение в тетради: № 4  2.Сравните с ответом на доске. 3.Поставьте отметку в табличке: если правильно + , если неправильно -. 4.Затем это уравнение 1 учащийся (по желанию) решает на доске. Вы сверяете своё решение, исправляете ошибки, если они есть, и ставите каждый себе оценку в табличке. 4.Подведение итогов. «5» - 18-21баллов; «4» - 14-17баллов; «3» - 10-13баллов. На первые 3 пункта отвечать: да или нет.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
–
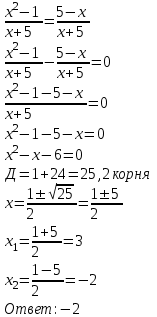
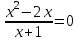
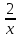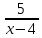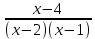
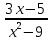=0
=0