РГР по Теории колебаний (резонансы в бурильной колонне). РГР_Теория_колебаний. Решение этого уравнения можно получить графически как совокупность точек пересечения двух функций (U и u условные единицы) 2)
 Скачать 94.83 Kb. Скачать 94.83 Kb.
|
|
1 Задание Требуется определить собственные частоты колебаний (продольных и крутильных) стальной колонны бурильных труб диаметром 54 мм СБТН-54 (D=0,054 м, d=0,045 м, Е=2∙1011 Па, удельная плотность материала труб 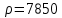 кг/м3, кг/м3, 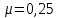 ) при бурении скважины до глубины 700 м с осевой нагрузкой С=10 кН станком УКБ-5П. ) при бурении скважины до глубины 700 м с осевой нагрузкой С=10 кН станком УКБ-5П.
2 Решение Резонансные частоты при колебаниях колонны бурильных труб имеют место при совпадении частот привода и частот собственных колебаний (продольных и крутильных) колонны труб. Продольные колебания колонны бурильных труб имеют место при изменении осевой нагрузки на забой, при котором наблюдается смещение отдельных сечений колонны вдоль ее продольной оси. Частотное уравнение для этого случая имеет вид: 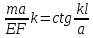 , (2.1) , (2.1)где m=C/g=1000 кг – сосредоточенная масса на нижнем конце колонны (в контакте с забоем), равная отношению осевой нагрузки С и ускорения силы тяжести; а – скорость продольной волны в материале колонны; Е – модуль упругости материала труб при растяжении – сжатии; F = площадь поперечного сечения колонны; l – ее длина, k – неизвестная частоты собственных колебаний колонны бурильных труб. Решение этого уравнения можно получить графически как совокупность точек пересечения двух функций (U и U* - условные единицы): 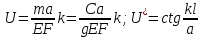 . (2.2) . (2.2)Частотное уравнение для крутильных колебаний получается аналогично уравнению (2.1) из волнового уравнения крутильных колебаний, откуда следует: 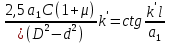 , (2.3) , (2.3)где а1 – скорость поперечной волны в материале колонны бурильных труб; k’ – неизвестная частота собственных крутильных колебаний колонны. По аналогии с продольными колебаниями введем следующие обозначения ( 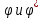 - условные единицы): - условные единицы):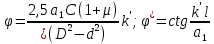 . (2.4) . (2.4)Для перевода частоты привода 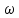 в частоту вращения колонны используется известное выражение: в частоту вращения колонны используется известное выражение: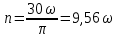 ,(2.5) ,(2.5)где n – частота вращения колонны бурильных труб, об/мин.    55,00 86,04 n, об/мин Расчеты по формулам (2.2 и 2.4) представим графически на рис. 1.            5,75 9 U* U ϕ* ϕ ω, с-1 ϕ, у.е. U, у.е. 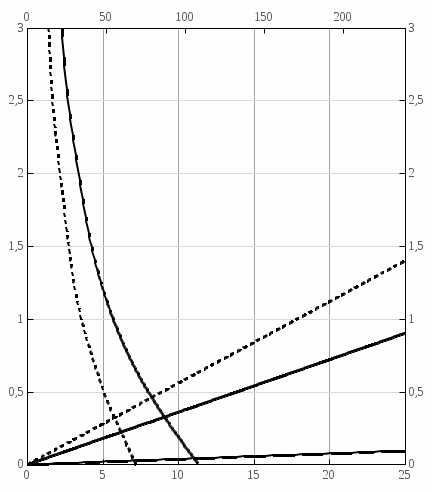 Рисунок 1. Резонансы при продольных (U, U*) и крутильных ( 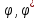 ) колебаниях колонны СБТН-54 при малых частотах вращения шпинделя ) колебаниях колонны СБТН-54 при малых частотах вращения шпинделяИз расчетов следует, что ω1=9 с-1 (n1=86 об/мин) и ω1’=5,75 с-1 (n1’= 55 об/мин). Составим таблицу для всех найденных точек по графику, изображенному на рис. 2 (см. приложение 1). В таблицу добавим также диапазоны частот ±10% от номинальных значений по паспорту установки, в которых могут появиться резонансные частоты. Таблица 1 – Результаты расчетов по формулам 2.2 и 2.4 графическим методом
Таким образом, резонансные частоты продольных колебаний колонны представлены в точках 2, 4, 6, 8. А резонансные частоты крутильных колебаний – в точках 4’, 5’, 6’, 9’, 10’, 11’, 12’, 13’. При появлении резонансов усиливаются амплитуды колебаний колонны, могущие вызвать обрывы самих труб и обрушение пород стенок скважины, что влечет за собой сложные аварии при бурении скважин. Приложение 1 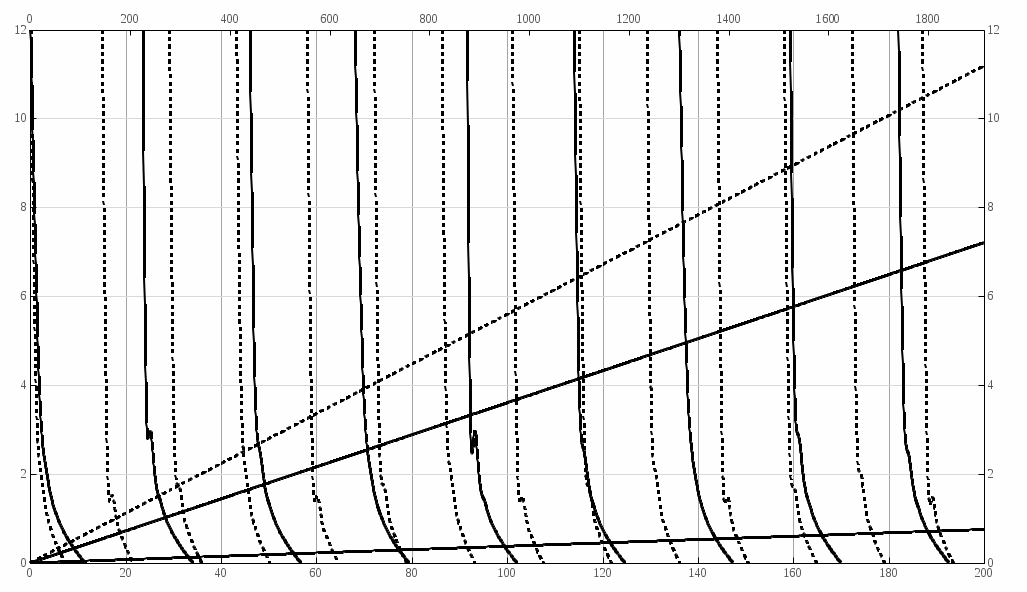 Рисунок 2. Резонансы при продольных (U, U*) и крутильных ( 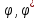 ) колебаниях колонны СБТН-54 на всем диапазоне частот вращения шпинделя буровой установки УКБ-5П ) колебаниях колонны СБТН-54 на всем диапазоне частот вращения шпинделя буровой установки УКБ-5П | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
