финансы 2 практическое. Решение Формула простых процентов имеет следующий вид где первоначальная сумма, руб., наращенная сумма, руб
 Скачать 18.11 Kb. Скачать 18.11 Kb.
|
Практическое задание 1Кредит размером 1,2 млн. руб. выдан 15 февраля до 7 ноября включительно под 17% годовых. Какую сумму должен вернуть должник в конце срока, если начисляются простые проценты. При решении задачи используйте три способа начисления процентов: первый способ: начисление точных процентов с точным числом дней ссуды; второй способ: начисление обыкновенных процентов с точным числом дней ссуды; третий способ: начисление обыкновенных процентов с приближенным числом дней ссуды. Решение: Формула простых процентов имеет следующий вид: 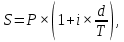 где 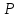 – первоначальная сумма, руб., – первоначальная сумма, руб.,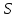 – наращенная сумма, руб., – наращенная сумма, руб.,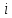 – годовая процентная ставка, доли единицы, – годовая процентная ставка, доли единицы,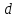 – количество дней пользования кредитом, – количество дней пользования кредитом,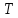 – временная база. – временная база.Осуществляем срок пользования кредитом: 1) если в расчет принимается точное число дней ссуды: 14 дней февраля (с 15 по 28-е число), 31 день марта, 30 дней апреля, 31 день мая, 30 дней июня, 31 день июля, 31 день августа, 30 дней сентября, 31 день октября, 7 дней ноября (с 1 по 7-е число). И из полученной суммы вычитаем единицу, поскольку дата выдачи и дата погашения кредита всегда считаются за один день. Суммируем и получаем: 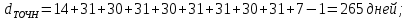 2) если в расчет принимается приближенное число дней ссуды: 14 дней февраля (с 15 по 28-е число), 8 месяцев (с марта по октябрь включительно) по 30 дней, 7 дней ноября (с 1 по 7-е число). Таким образом: 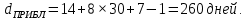 Первый способ – это английская практика начисления процентов. В данном случае осуществляется начисление точных процентов с точным числом дней ссуды. Это означает, что период начисления процентов равен фактическому сроку ( 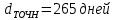 ), продолжительность года Т=365 дней. Наращенная сумма кредита равна: ), продолжительность года Т=365 дней. Наращенная сумма кредита равна: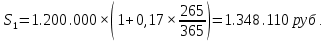 Второй способ – это французская практика, когда начисление обыкновенных процентов осуществляется с учетом точного числа дней ссуды. Это означает, что период начисления процентов равен фактическому сроку ( 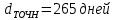 ), продолжительность года Т=360 дней. Наращенная сумма кредита равна: ), продолжительность года Т=360 дней. Наращенная сумма кредита равна: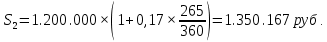 Третий способ – это немецкая практика, когда начисление обыкновенных процентов с учетом приближенного числа дней ссуды. Это означает, что один полный месяц равен 30 дням ( 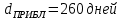 ), продолжительность года Т=360 дней. Наращенная сумма кредита равна: ), продолжительность года Т=360 дней. Наращенная сумма кредита равна: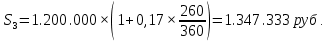 Таким образом, если используется английская практика начисления процентов, заемщик должен вернуть банку 1 348 110 руб.; если французская практика – 1 350 167 руб.; если немецкая практика – 1.347.333 руб. |
