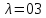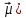финансовая математика. Финансовая математика контрольная. Высшего образования финансовый университет при правительстве российской федерации
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕОБРАЗОВАТЕЛЬНОЕБЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ А  ЛТАЙСКИЙ ФИЛИАЛ ЛТАЙСКИЙ ФИЛИАЛПо дисциплине «Финансовая математика» Студент _________________________ Пастухова Алёна Сергеевна(подпись) Группа18-1Б-ЭК02 Номер личного дела 100.02/180084Преподаватель канд.тех.наук, Жевнов Денис АнатольевичБарнаул 2021  Решение. По условию задачи Денежная сумма – разовая, проценты – простые. P=11000, S=12000 Период начисления 8 месяцев. Формула наращения для простых процентов: 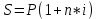 , где , гдеS – наращенная сумма в конце срока; Р – первоначальная сумма; n – срок ссуды (в годах); i – процентная ставка. Выделим из формулы наращения процентную ставку: i = (S/P-1)*n. Воспользуемся формулой наращения по простым процентам в MS Excel ( 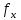 / Дата и время / ДОЛЯ ГОДА). Найдем значение n, учитывая, что вклад на 8 месяцев. В банке используются точные проценты с точным числом дней ссуды (английская практика). / Дата и время / ДОЛЯ ГОДА). Найдем значение n, учитывая, что вклад на 8 месяцев. В банке используются точные проценты с точным числом дней ссуды (английская практика).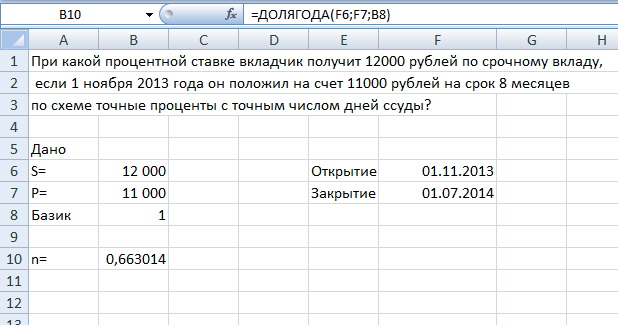 Рис. 1. Расчет доли года. Теперь определим процентную ставку по формуле i = (S/P-1)*n. Вставим формулу в ячейку В12. 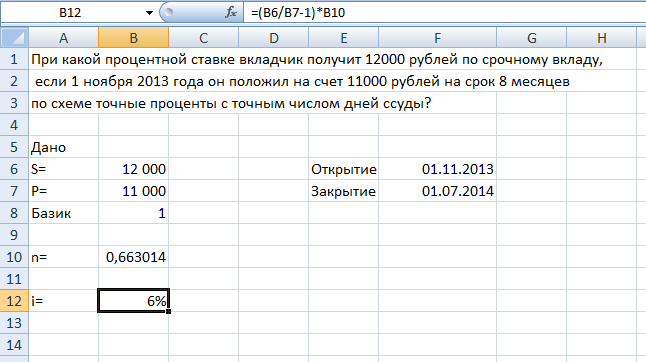 Рис.2. Расчет процентной ставки. Ответ: процентная ставка 6%.  Решение. Согласно условию задачи рассматривается операция наращения разовой суммы Р по номинальной процентной ставке j=9,5%. Величина Р не задана, соответствующая наращенная сумма S=100 000. Срок операции n=2.5 года, m=12(ежемесячное начисление процентов). Воспользуемся финансовой функцией ПС (Ставка; Кпер; Плт; Бс; Тип). Расчеты будем производить в MS Excel. Ставка – процентная ставка за период 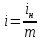 ; ;Кпер – общее число периодов платежей по аннуитету 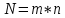 ; ;Плт – выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ренты; Бс – требуемое значение будущей стоимости или остатка средств после последней выплаты; 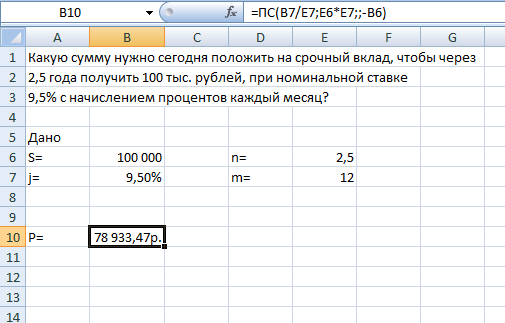 Рис.3. расчет первоначальной суммы вклада Ответ: сумма которую нужно положить на срочный вклад 78 933,47р.  Решение. Для нахождения суммы, которую получит векселедержатель будем использовать финансовую функцию ПС (Ставка; Кпер; Плт; Бс; Тип) в Excel. По условию задачи: S = 60000 рублей, j= 8,6%, n = 1,5, m=2. 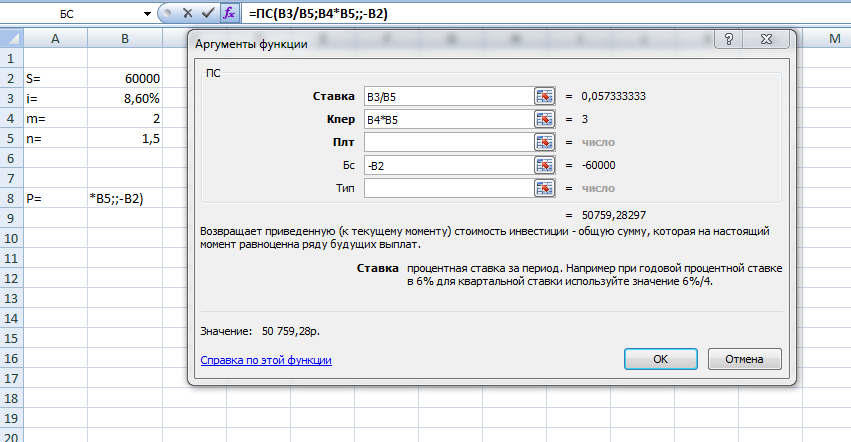 Рис. 3.1. Расчет денежной суммы, которую получит векселедержатель Ответ: Векселедержатель получит 50 759,28 руб  Решение. Денежная сумма –переодические платежи: R=5000 Срок n=15 лет. Проценты сложные, j=10%, m=12 раз в год. Для расчета цены, по которой был приобретен станок воспользуемся стандартной финансовой функцией ПС (Ставка; Кпер; Плт; Бс; Тип). 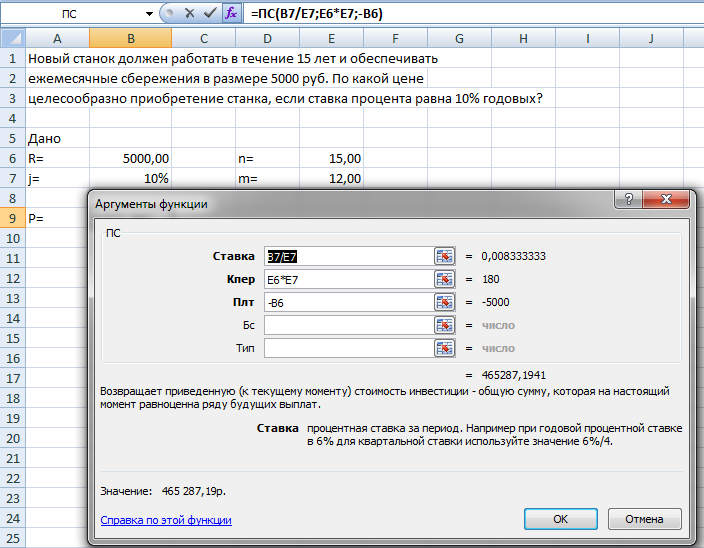 Рис.4 Расчет цены приобритения станка. Ответ: целесообразно приобрести станок по 465 287,19р.   Решение. Найдем матрицу рисков. Каждый элемент матрицы рисков определяется равенством 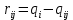 , т.е. получается вычитанием данного элемента , т.е. получается вычитанием данного элемента 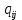 из максимального в каждом столбце. из максимального в каждом столбце.Решение проведем с помощью Excel. В ячейку В7 введем функцию =МАКС(В3:В6) и скопируем ее в ячейки С7:F7. 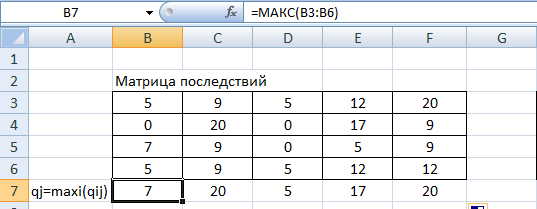 Рис.5. Определение максимального элемента. Получили: q1 = 7; q2 = 20; q3 = 5; q4 = 17; q5 = 20. Найдем каждый элемент матрицы рисков с помощью равенства 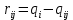 Например, для j-1 получим: 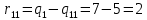 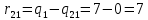 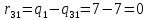 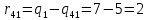 Все вычисления выполним в Excel. Так для элемента r11 в ячейке Н3 будет функция для вычисления =$В7$-В3. Для элемента r12 в ячейке I3 будет функция =$C7$-C3, Для элемента r13 в ячейке J3 будет функция =$D7$-D3, Для элемента r14 в ячейке K3 будет функция =$E7$-E3, Для элемента r15 в ячейке L3 будет функция =$F7$-F3. Формулы ячеек H3:L3 скопируем в соответствующие ячейки. И получим матрицу рисков. 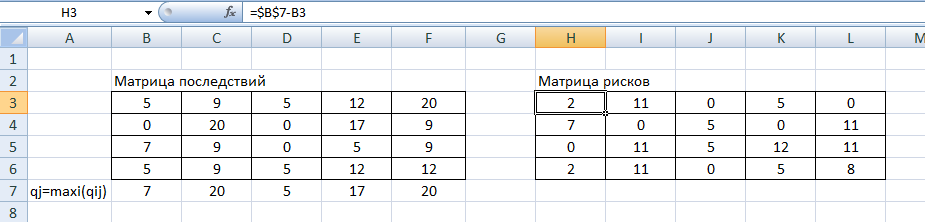 Рис.6. Результаты вычислений. Матрица рисов имеет вид: R= 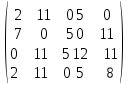 Проведите анализ ситуации полной неопределенности, применив правила по принятию решений Вальда, Сэвиджа и Гурвица (взять λ равному 0,5; 0,4 и 0,3). Определим решение по правилу Вальда. Проанализируем каждое решение, т.е в каждой строке матрицы Q найдем 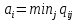 - самый маленький, но гарантированный доход. - самый маленький, но гарантированный доход.Правило Вальда рекомендует выбрать решение i0 с наибольшим ai : i0 =maxi(minjqij) В каждой строке матрицы Q найдем минимальное значение. В ячейку В10 введем функцию =МИН(B3:F3) и скопируем ее в ячейки В11, В12 и В13. 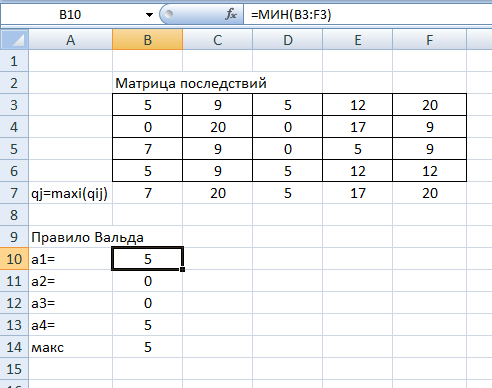 Рис.7. Результаты расчетов по правилу Вальда Получили: а1 = 5, а2 = 0, а3 = 0, а4 = 5. Среди всех чисел аi выберем наибольшее. Наибольшее значение а1 = а4 =5. Значит, правило Вальда рекомендует принять первое или четвертое решение. Определим решение по правилу Сэвиджа(правило минимального риска). Правило Сэвиджа рекомендует принять решение 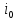 с наименьшим с наименьшим 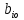 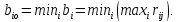 Рассматривая каждое решение, в каждой строке матрицы R найдем максимальный риск 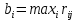 . . Расчеты выполним в Excel. В ячейку G10 введем функцию =МАКС(H3:L3) и скопируем ее в ячейки G11, G12 и G13. Получили: 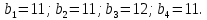 Выберем наименьшее 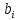 . Наименьшее значение . Наименьшее значение 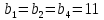 . .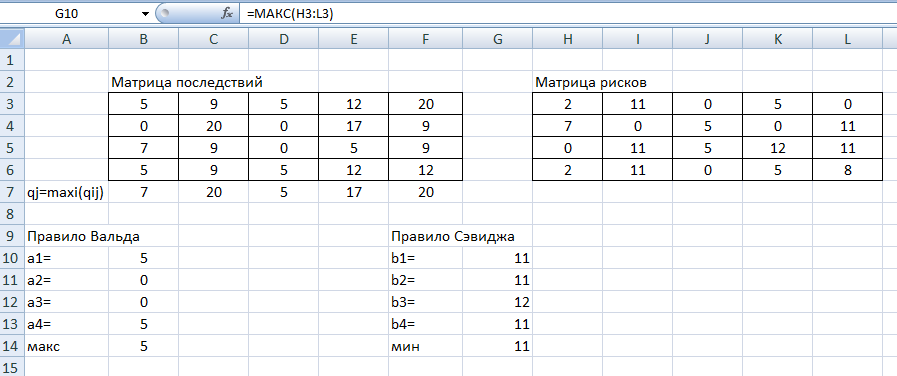 Рис.8. Результаты расчетов по правилу Сэвиджа. Правило Сэвиджа рекомендует принять первое, второе и четвертое решение. Применим правило Гурвица. (взять λ равному 0,5; 0,4 и 0,3). По правилу Гурвица взвешиваются пессимистический и оптимистический подходы и принимается решение i, при котором достигается максимум 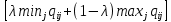 Рассмотрим различные значения 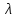 : :При 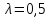 . .Проанализируем каждое решение. Для каждой строки матрицы Q вычислим величину параметра  . Для этого в ячейку В18 введем функцию =$B$17*МИН(B3:F3)+(1-$B$17)*МАКС(B3:F3). . Для этого в ячейку В18 введем функцию =$B$17*МИН(B3:F3)+(1-$B$17)*МАКС(B3:F3).И скопируем ее в ячейки В19, В20 и В21. Получили: 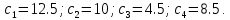 Максимальное значение 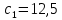 . .Следовательно, при 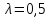 , правило Гурвица рекомендует первое решение. , правило Гурвица рекомендует первое решение.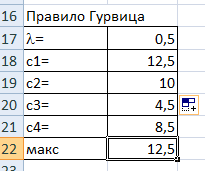 Рис.9 Аналогично проведем вычисления для остальных значений 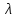 . .При 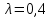 . .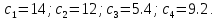 Максимальное значение 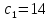 . . При 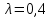 , правило Гурвица рекомендует первое решение. , правило Гурвица рекомендует первое решение.При 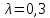 . .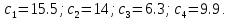 Максимальное значение 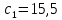 . .При 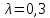 , правило Гурвица рекомендует первое решение. , правило Гурвица рекомендует первое решение.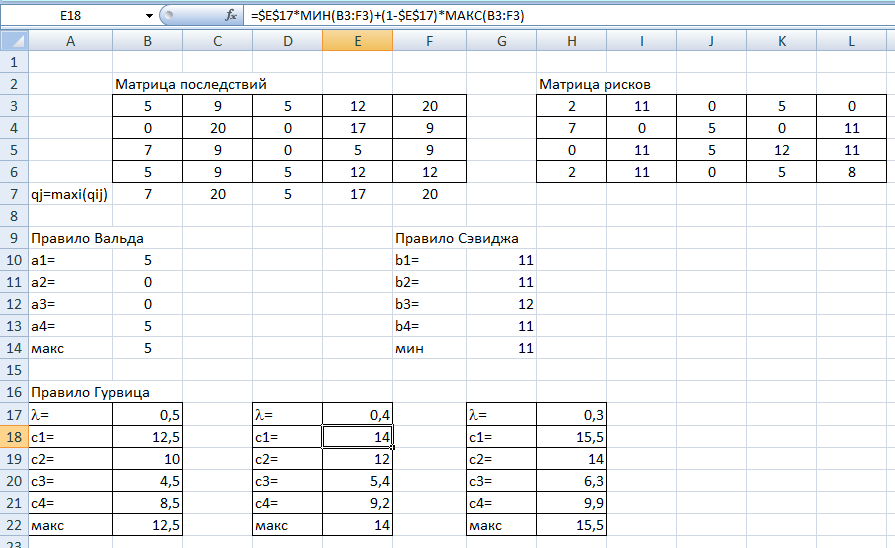 Рис.10. Результаты вычисление по правилу Гурвица Примененные правила не дают однозначной рекомендации. В таких случаях выбирается то решение, которое рекомендуется чаще других. Рекомендации оформим в виде таблицы.
Однозначно нужно выбрать первое решение. 3)Проведите анализ ситуации частичной неопределенности при известных вероятностях того, что реальная ситуация развивается по варианту j: 0,25; 0,2; 0,3; 0,15; 0,1 (примените правила максимизации среднего ожидаемого дохода и минимизации среднего ожидаемого риска). Решение сделаем в Excel. Подготовим матрицы последствий и рисков и введем вероятности того, что реальная ситуация развивается по варианту j: 0,25; 0,2; 0,3; 0,15; 0,1 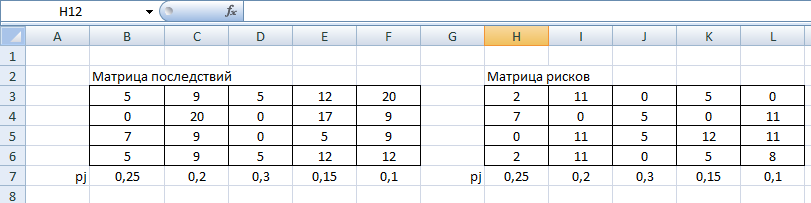 Рис. 11 Применим правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-го решения, является случайной величиной 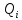 , с рядом распределения , с рядом распределения 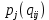 . Математическое ожидание . Математическое ожидание 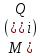 и есть средний ожидаемый доход, обозначаемый также и есть средний ожидаемый доход, обозначаемый также 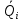 . Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход. . Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.Найдем средний ожидаемый доход для каждого решения при указанных вероятностях. Для этого в ячейку C10 введем функцию: =СУММПРОИЗВ($B$7:$F$7;B3:F3) и скопируем ее в ячейки C11, C12, C13. Получим: М(Q1) = 8,35; М(Q2) = 7,45; М(Q3) = 5,2; М(Q4) = 7,55. Определили, что максимальный средний ожидаемый доход равен 8,35 и соответствует первому решению. 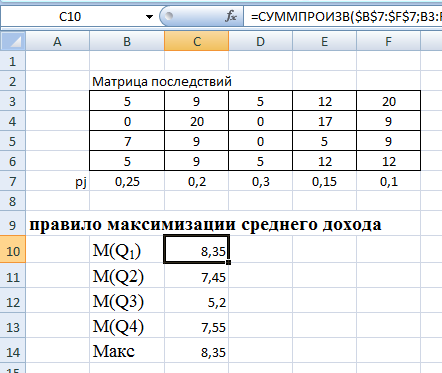 Рис.12. Результаты расчетов по правилу максимизации среднего ожидаемого дохода. Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-го решения является случайной величиной 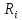 рядом распределения рядом распределения 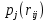 . Математическое ожидание, . Математическое ожидание, 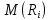 и есть средний ожидаемый риск, обозначаемый также и есть средний ожидаемый риск, обозначаемый также 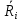 . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск. . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.Вычислим средние ожидаемые риски при указанных вероятностях для каждого решения. В ячейку I10 введем функцию: =СУММПРОИЗВ($H$7:$L$7;H3:L3) и скопируем ее в ячейки I11, I12, I13. Получим средние риски: М(R1) = 3,45; М(R2) = 4,35; М(R3) = 6,6; М(R4) = 4,25. Правило рекомендует принять решение, влекущее минимальный средний риск. Минимальный средний риск равен 3,45 и соответствует первому решению. 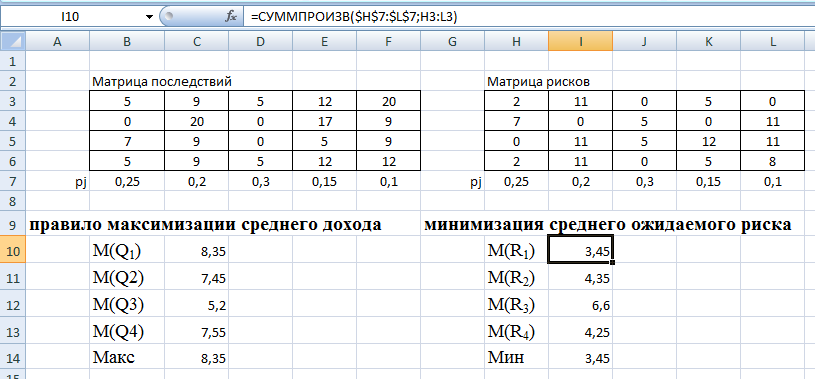 Рис.13. Результаты расчетов по правилу минимизации среднего ожидаемого риска. В условиях частичной неопределенности нужно выбирать только первое решение.  Решение. Портфель минимального риска с заданной доходностью находится по формуле Х = V-1(λI + ν 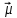 ). ).Для нахождения портфеля предварительно надо вычислить: - обратную матрицу V-1; - константы (при этом константы α, γ, 𝛿 – положительные числа): - α = ITV-1I, β = ITV-1 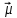 = = 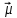 TV-1I, TV-1I,- γ = 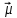 TV-1 TV-1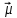 , 𝛿 = αγ – β2; , 𝛿 = αγ – β2;- λ = 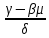 ; ν = ; ν = 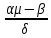 . .Вычисления проведем в Excel. Внесем исходные данные. Р  ис.14. Исходные данные ис.14. Исходные данныеВведем зависимости. Уравнение минимальной границы имеет вид: σ = 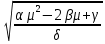
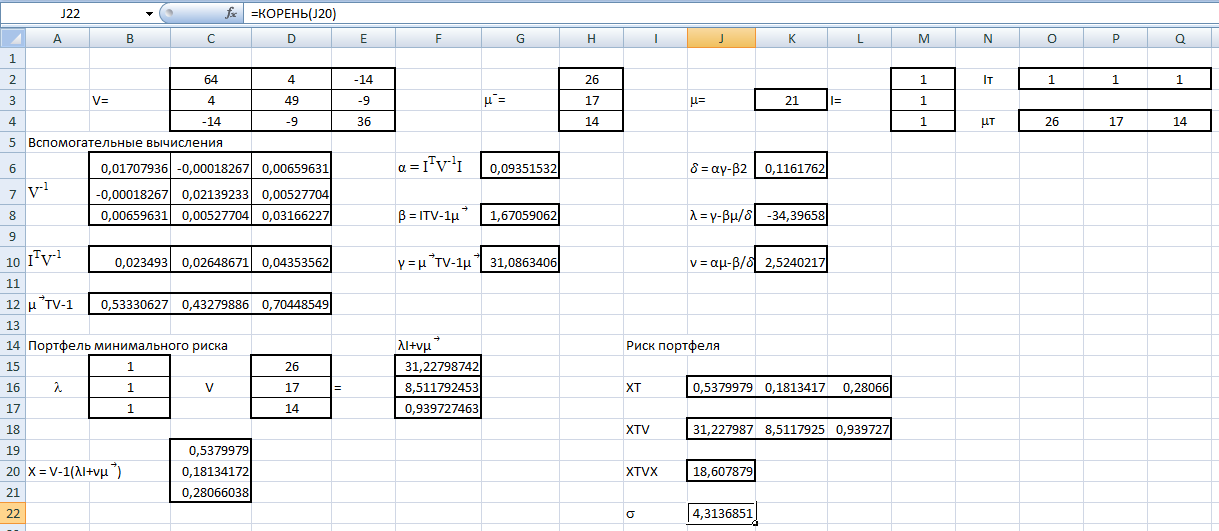 Рис.15. Результаты расчета портфеля минимального риска Получили: Х = (0,538; 0,181; 0,281). Чтобы обеспечить доходность портфеля 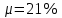 необходимо взять 53,8% бумаг первого вида; 18,1% - второго и 28,1% - третьего вида. необходимо взять 53,8% бумаг первого вида; 18,1% - второго и 28,1% - третьего вида.Риск каждой бумаги определим по ковариационной матрице: по диагонали стоят дисперсии, поэтому для рисков бумаг имеем: 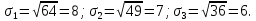 Риск портфеля равен 4,31 и оказался меньше риска первой бумаги (σ1=8), второй (σ1=7) и третьей (σ1=6) бумаг. При этом доходность портфеля μ=21% на 5% меньше доходности первой бумаги, на 4% больше доходности второй и на 7% больше доходности третьей бумаги. Уравнение минимальной границы имеет вид: σ = 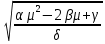 Подставляя в нее найденные значения констант α=0,09; β=1,67; γ=31,09; 𝛿=0,12 получим σ = 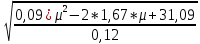 = = 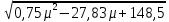 . .Итак, минимальная граница имеет вид σ = 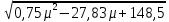 . . Решение. При ρ1 = 0,3, q1 = 150, К1 = 108; ρ2 = 0,2, q2 = 70, К2 = 104, m=2 воспользуемся формулой ρ = 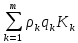 / / 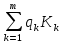 , где , где ρk – доходность облигации, qk – количество облигаций данного вида, Kk – курс облигации. Вычисления выполним в Excel. 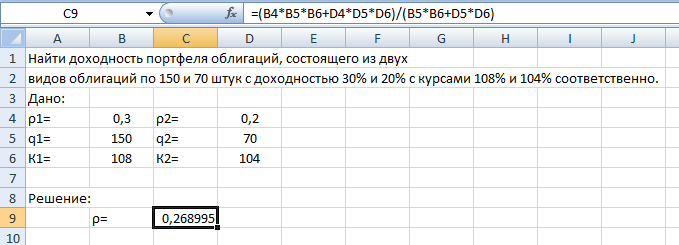 Рис.16. Результаты вычислений поиска доходности портфеля облигаций Ответ: Доходность портфеля облигаций равна ρ ≈ 0,269.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||