Решение. Графический метод
 Скачать 93.52 Kb. Скачать 93.52 Kb.
|
|
Решить задачу ЛП графически, симплекс-методом, в среде Microsoft Excel: 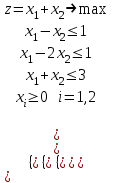 . .Решение. 1. Графический метод. Первый шаг при использовании графического метода заключается в геометрическом представлении допустимых решений, т. е. строении области (допустимых) решений, в которой одновременно удовлетворяются все ограничения модели. Искомая область (пространство) решений показана на рисунке. Условия не отрицательности переменных 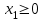 и и 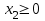 ограничивают область их допустимых значений первым квадрантом (представляющим собой по определению часть плоскости, расположенную над осью ограничивают область их допустимых значений первым квадрантом (представляющим собой по определению часть плоскости, расположенную над осью 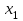 и правее оси и правее оси 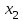 ). Другие границы пространства решений изображены на плоскости ). Другие границы пространства решений изображены на плоскости 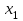 , , 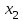 прямыми линиями, построенными по уравнениям, которые получаются при замене знака ≤ на знак = в остальных ограничениях. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных. Полученное таким образом пространство решений – многоугольник прямыми линиями, построенными по уравнениям, которые получаются при замене знака ≤ на знак = в остальных ограничениях. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных. Полученное таким образом пространство решений – многоугольник 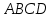 – показан на рисунке. – показан на рисунке.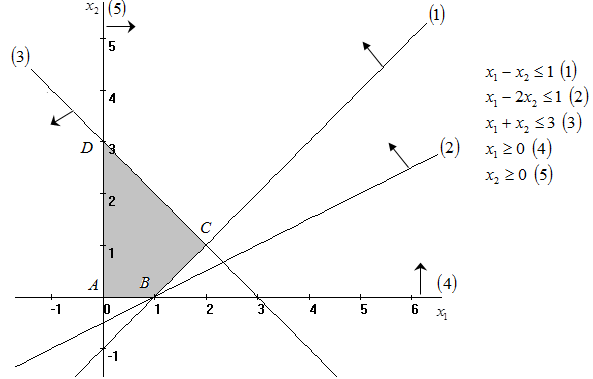 В каждой точке, принадлежащей внутренней области или границам многоугольника решений 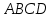 , все ограничения выполняются, поэтому решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, но, несмотря на это, можно найти оптимальное решение, если выяснить, в каком направлении возрастает целевая функция модели , все ограничения выполняются, поэтому решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, но, несмотря на это, можно найти оптимальное решение, если выяснить, в каком направлении возрастает целевая функция модели 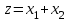 . На рисунке показано, как осуществляется такая операция. На график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение. . На рисунке показано, как осуществляется такая операция. На график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение. На рисунке были использованы следующие значения целевой функции: z=1 и z=3. Чтобы найти оптимальное решение, следует перемещать прямую в направлении возрастания целевой функции до тех пор, пока она не сместится в область недопустимых решений. На рисунке видно, что оптимальному решению соответствует бесконечное множество точек отрезка 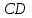 . Для вычисления оптимального (максимального) значения целевой функции вычислим ее значение в любой точке отрезка, например в точке . Для вычисления оптимального (максимального) значения целевой функции вычислим ее значение в любой точке отрезка, например в точке 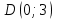 : : 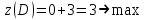 . .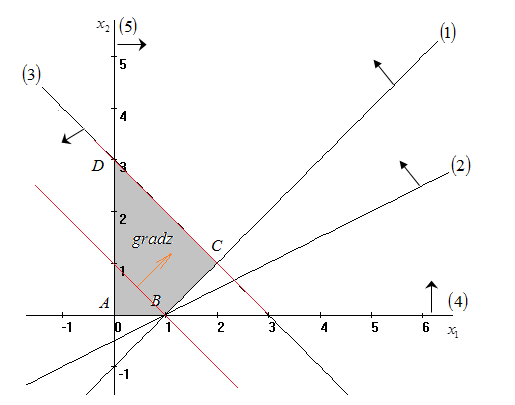 2. Симплекс-метод. Вводим в базис три вспомогательные базисные переменные 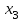 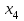 , , 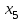 и записываем полученную каноническую модель задачи линейного программирования: и записываем полученную каноническую модель задачи линейного программирования: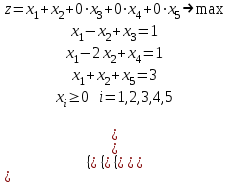 Строим первоначальную симплексную таблицу.
Поскольку имеем задачу на максимум и в оценочной строке есть отрицательные числа, то начальное опорное решение можно улучшить. Для этого переходим к следующей симплексной таблице. 1. Находим ключевой столбец (по наименьшему отрицательному числу в оценочной строке) – 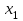 . .2. Для выбора ключевого элемента составляем отношение плановых значений к соответствующим положительным числам ключевого столбца и выбираем наименьшее число. В нашем случае ключевая строка – первая, поэтому ключевой элемент равен 1. 3. Вместо базисной неизвестной 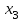 вводим вводим 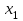 . .4. Формально заполняем базисные столбцы. 5. Заполняем ключевую строку (делим соответствующие числа на ключевой элемент). 6. Все другие строки заполняем методом Жордана-Гаусса.
1. Находим ключевой столбец (по наименьшему отрицательному числу в оценочной строке) – 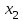 . .2. Для выбора ключевого элемента составляем отношение плановых значений к соответствующим положительным числам ключевого столбца и выбираем наименьшее число. В нашем случае ключевая строка – третья, поэтому ключевой элемент равен 2. 3. Вместо базисной неизвестной 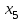 вводим вводим 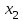 . .4. Формально заполняем базисные столбцы. 5. Заполняем ключевую строку (делим соответствующие числа на ключевой элемент). 6. Все другие строки заполняем методом Жордана-Гаусса.
В оценочной строке симплексной таблицы нет отрицательных значений, но для небазисной переменной 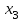 получилась нулевая оценка, то задача имеет бесконечное множество оптимальных решений. получилась нулевая оценка, то задача имеет бесконечное множество оптимальных решений.Из последней симплексной таблицы выписываем оптимальное решение: 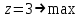 . . |
