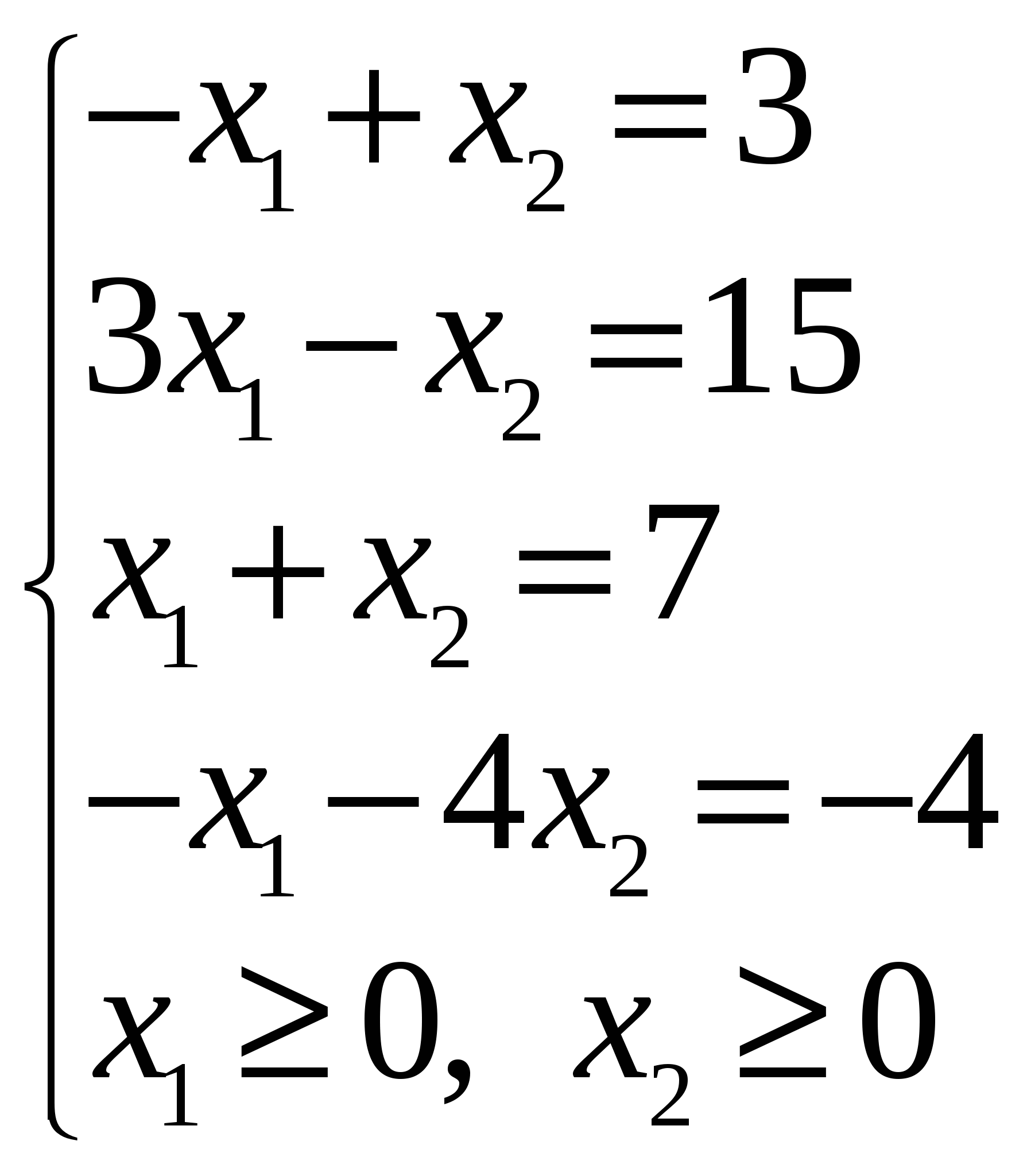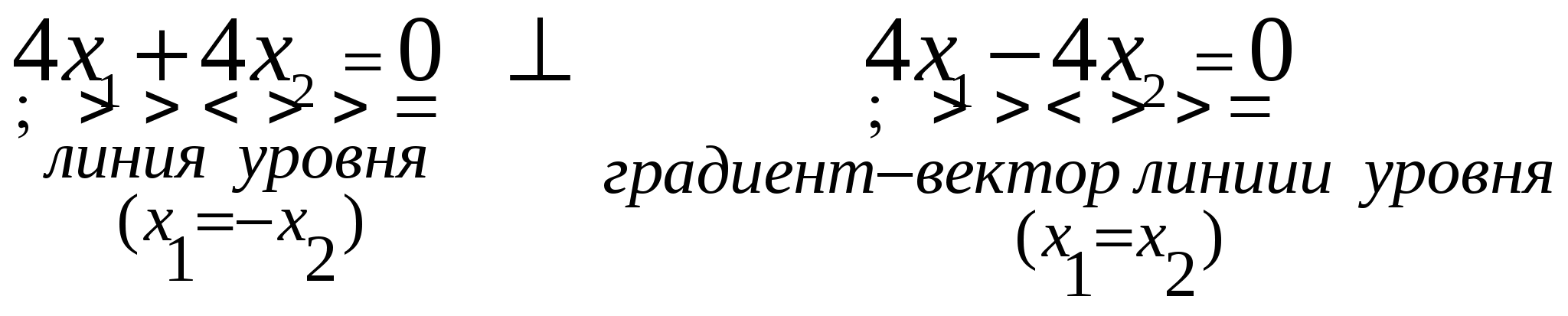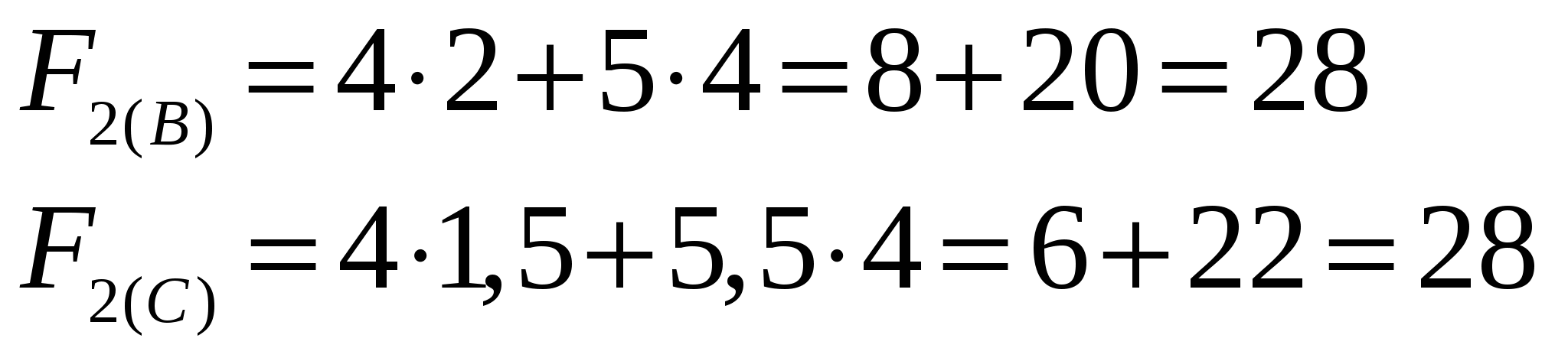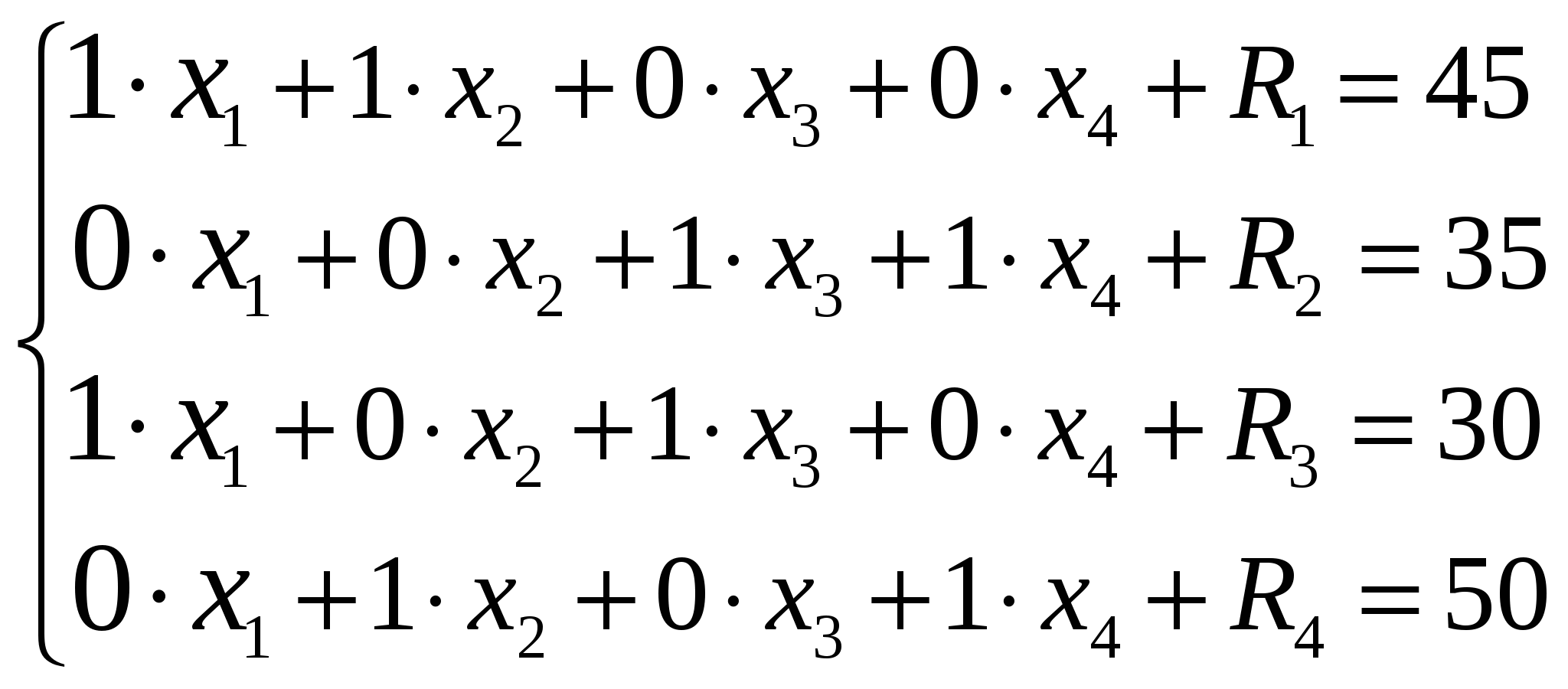Найти область допустимых решений Задачи Линейного Программирования из п.3
Построить линии уровня целевой функции Задачи Линейного программирования и вектор, показывающий направление роста целевой функции (отдельно для целевых функций из п. 3 А) и п.3 В).
Решить ЗЛП графическим методом. Выписать оптимальное решение, если оно существует, и оптимальное значение целевой функции.
а) 

б) 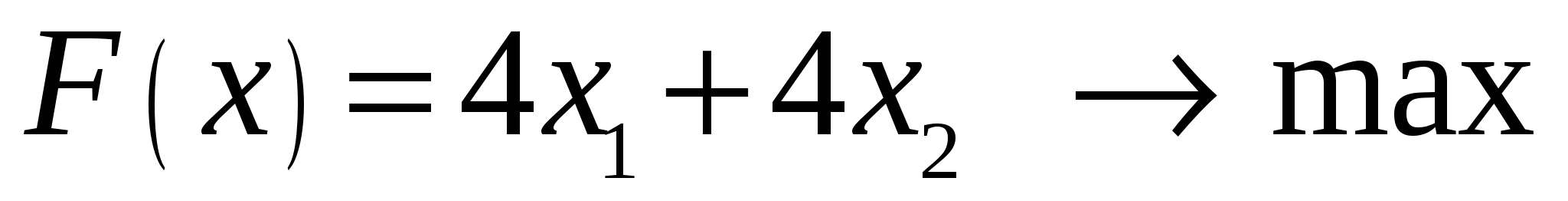 . При тех же ограничениях. . При тех же ограничениях.
Решить сбалансированную Транспортную Задачу. На складах  и и 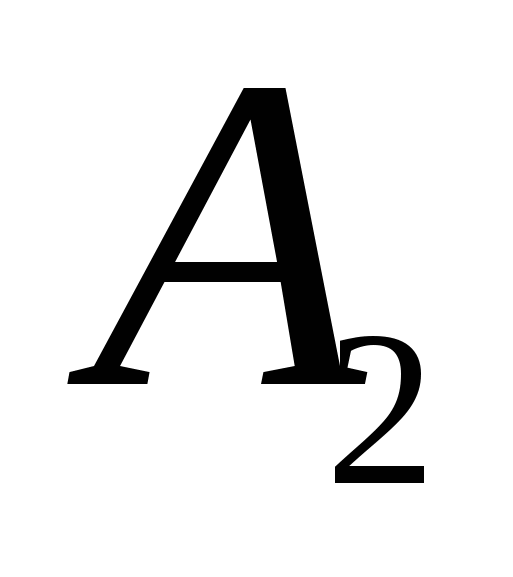 есть в наличии соответственно 45 и 35 тыс.ед. продукции. Два потребителя есть в наличии соответственно 45 и 35 тыс.ед. продукции. Два потребителя 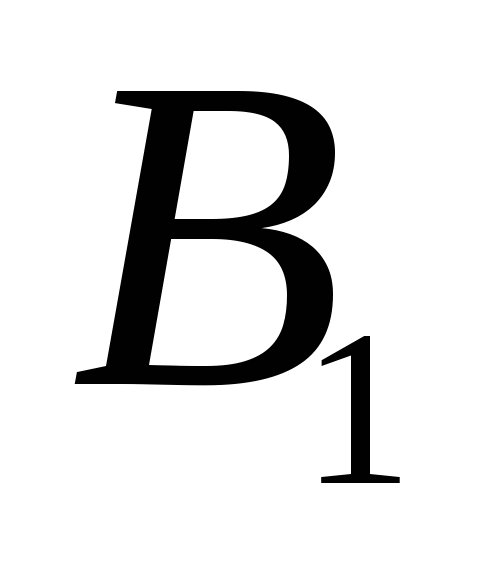 и и  хотели бы получить со склада соответственно 30 и 50 тыс.ед. продукции. Стоимость перевозки продукции с хотели бы получить со склада соответственно 30 и 50 тыс.ед. продукции. Стоимость перевозки продукции с  -го склада -го склада  -му потребителю задана матрицей -му потребителю задана матрицей  , где , где  - стоимость перевозки 1 тыс.ед.продукции в млн.руб. Как минимизировать стоимость перевозок? Найти оптимальное решение и значение целевой функции. - стоимость перевозки 1 тыс.ед.продукции в млн.руб. Как минимизировать стоимость перевозок? Найти оптимальное решение и значение целевой функции.
Написать ЗЛП, двойственную к ЗПЛ из п.3. Найти оптимальное решение и значение целевой функции, используя Теоремы двойственности.
№1.2.3.
Решение:
Строится многоугольная область допустимых значений на плоскости 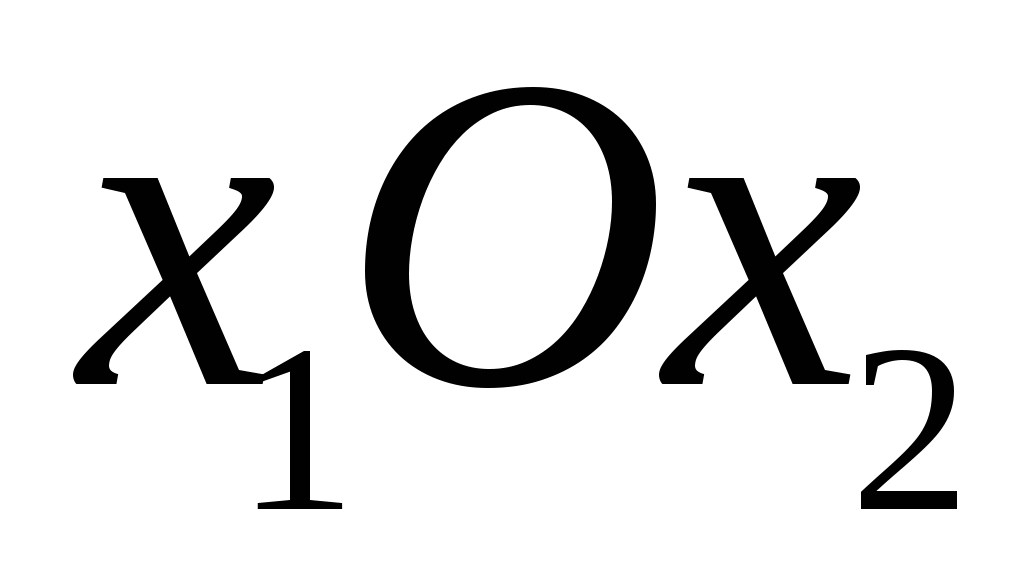 (рис.1) (рис.1)

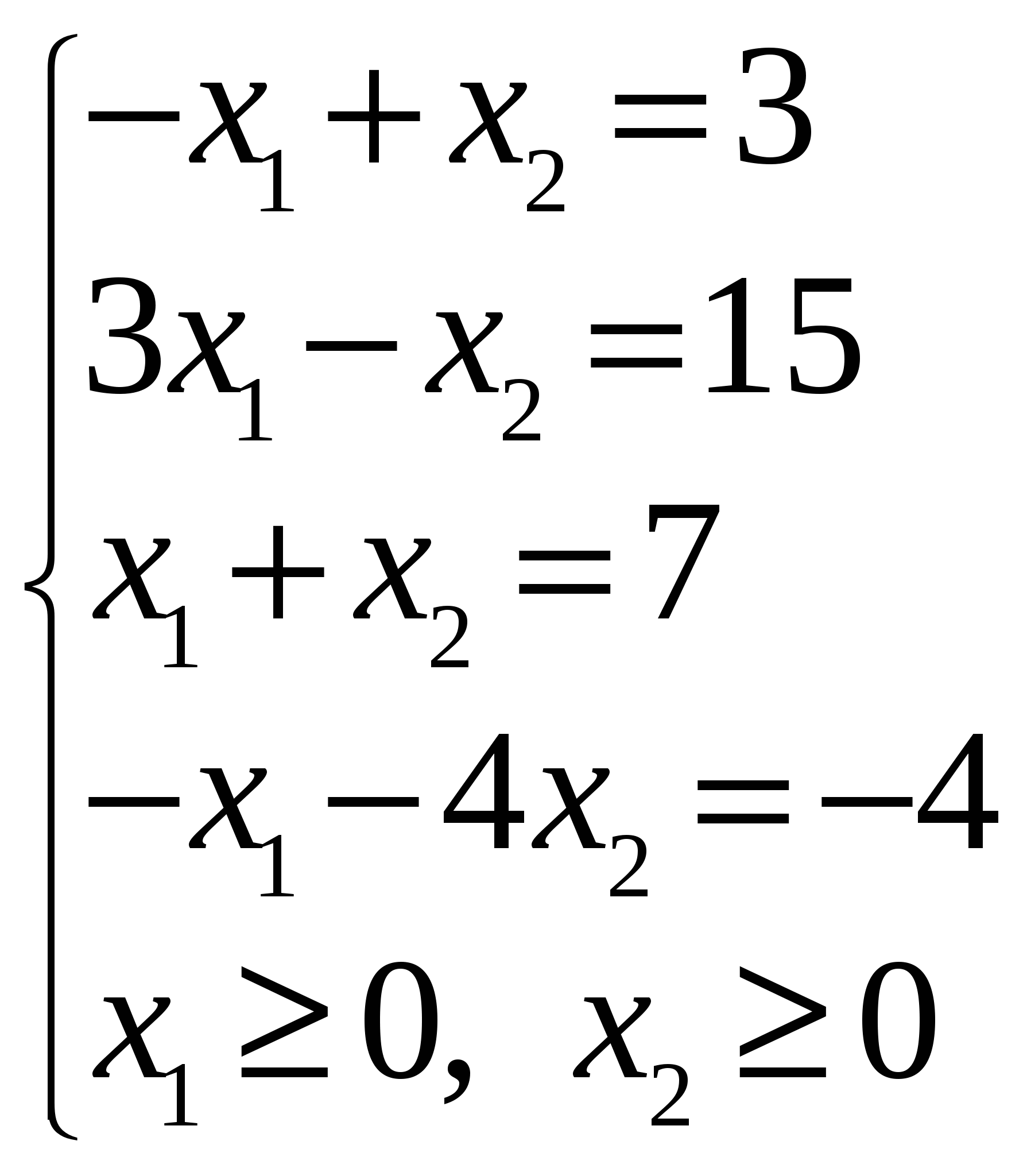
I-прямая

II –прямая

III –прямая

IV –прямая

Заштрихуем общую область допустимых значений (АВСDEF)
Приравняем целевую функцию 
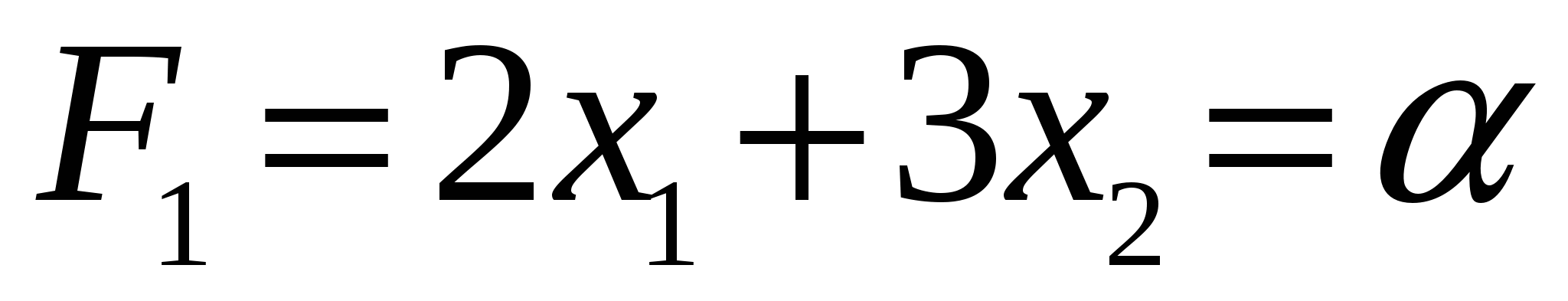 - линии уровня. - линии уровня.
Меняя значение  , получим семейство параллельных прямых, каждое из которых называется линией уровня. , получим семейство параллельных прямых, каждое из которых называется линией уровня.

Пусть 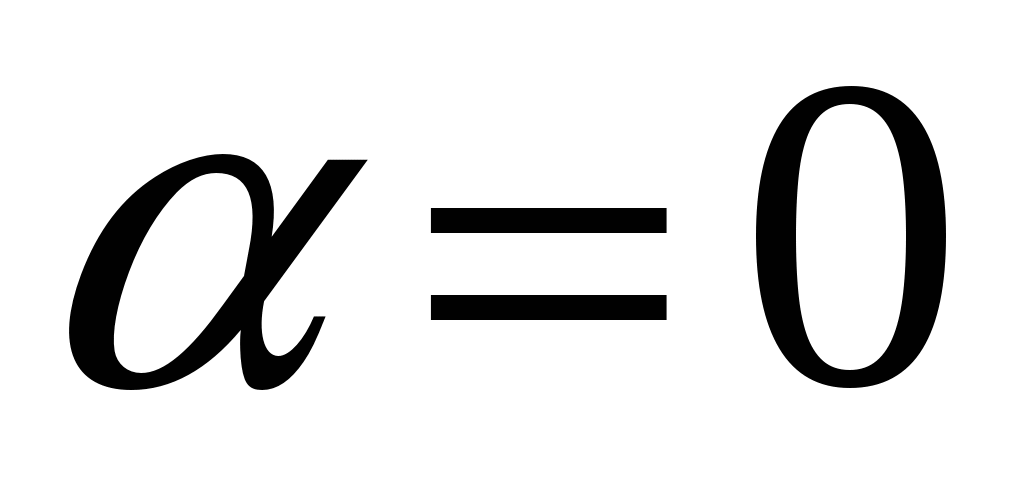 , вычислим координаты 2-х точек: , вычислим координаты 2-х точек:

Итак, линия уровня  перпендикулярна вектору-градиенту перпендикулярна вектору-градиенту  передвигается параллельно самой себе в направлении вектора градиента в случае задачи на ″ передвигается параллельно самой себе в направлении вектора градиента в случае задачи на ″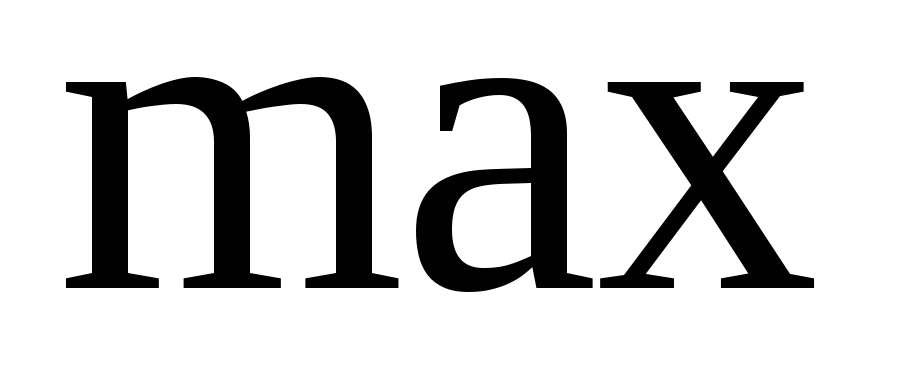 ″ до тех пор, пока линия уровня не покинет область допустимых значений (АВСDEF). ″ до тех пор, пока линия уровня не покинет область допустимых значений (АВСDEF).
Предельная точка (или точки) области являются оптимальными точками.
Градиент-вектор  целевой функции. целевой функции.
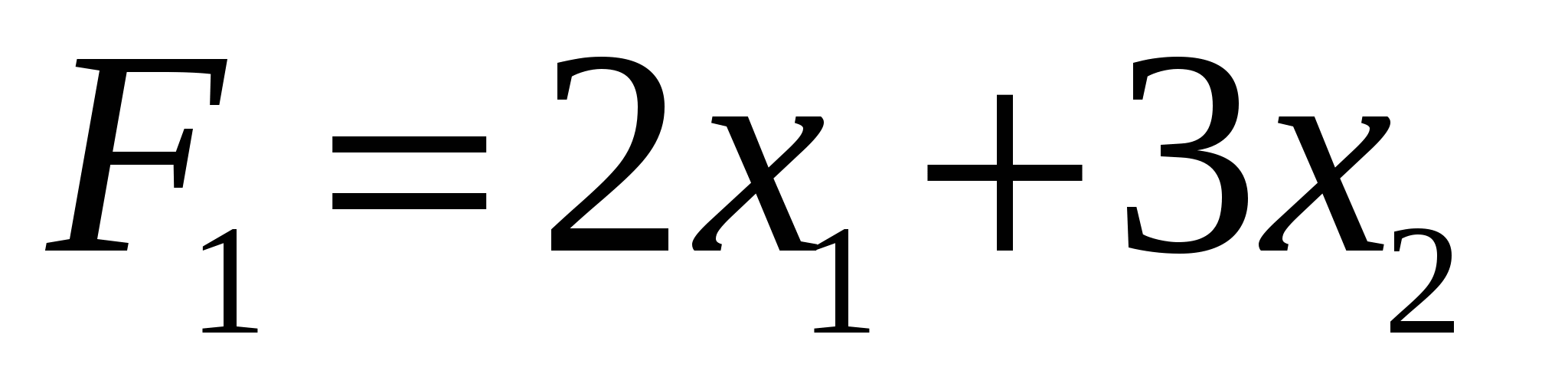 
Чтобы построить вектор-градиент  нужно соединить две точки нужно соединить две точки 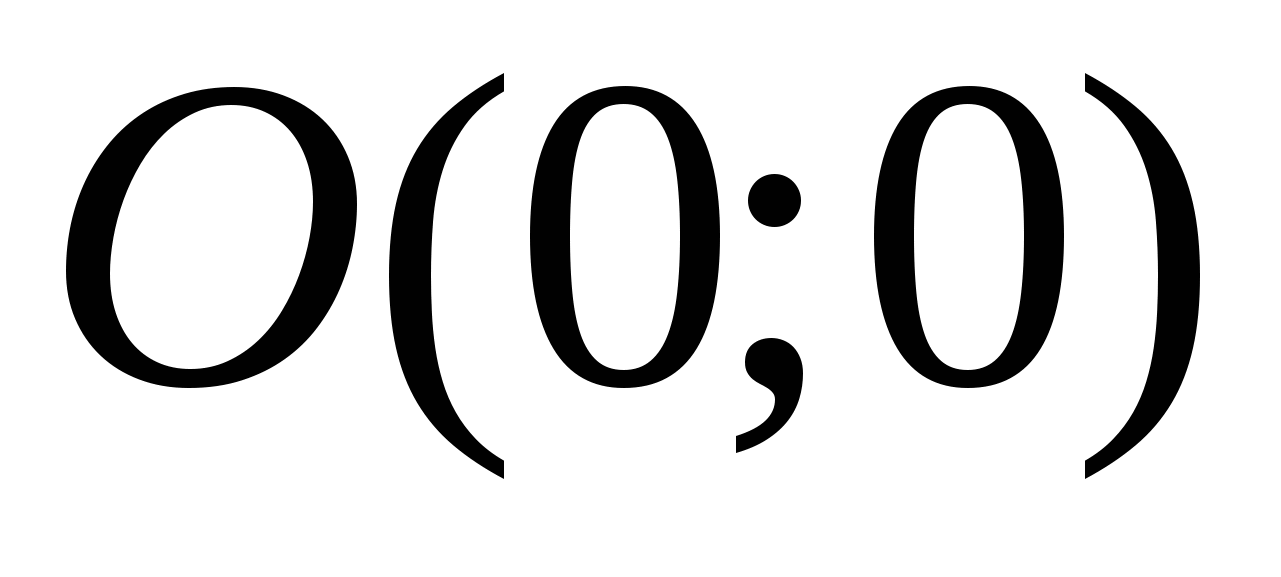 и и  . .
Уравнение  , ,   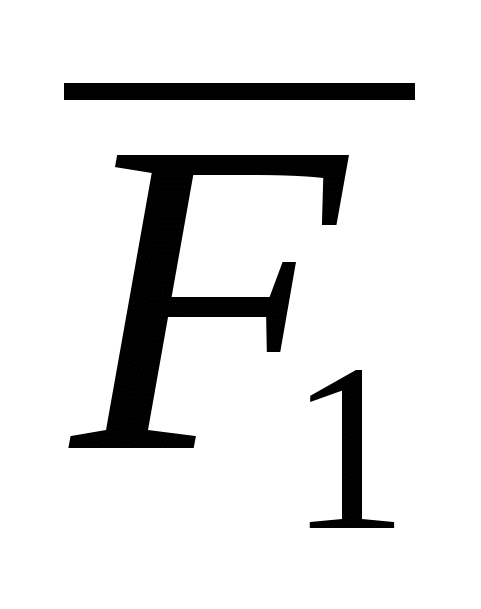

3) Чтобы найти координаты оптимальной точки, надо решить систему уравнений, которая соответствует прямым, пересечение которых образует эту точку. Значение целевой функции в этой точке будет оптимальным, а сами координаты являться решением задачи Л.П.
Обратим внимание, что при движении линии уровня  по направлению вектора-градиента по направлению вектора-градиента  в сторону ″ в сторону ″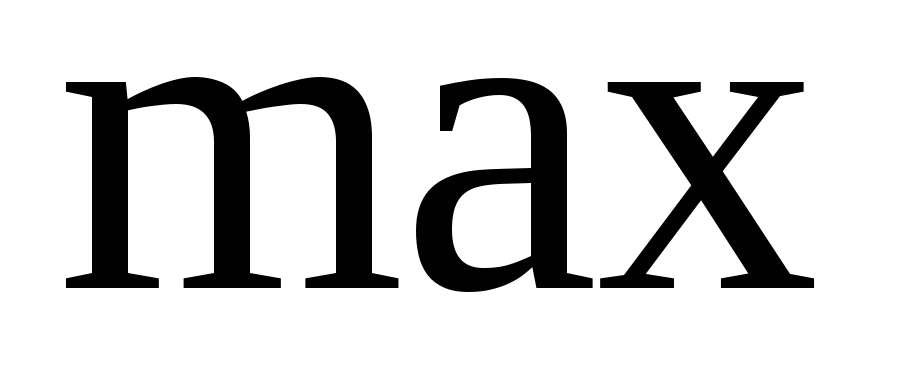 ″ целевой функции, ″ ″ целевой функции, ″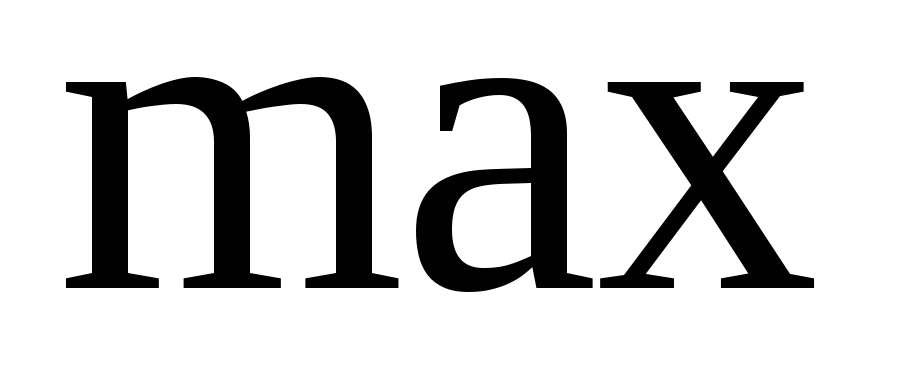 ″ значение находится в точке В пересечения прямых АВ и ВС. ″ значение находится в точке В пересечения прямых АВ и ВС.
 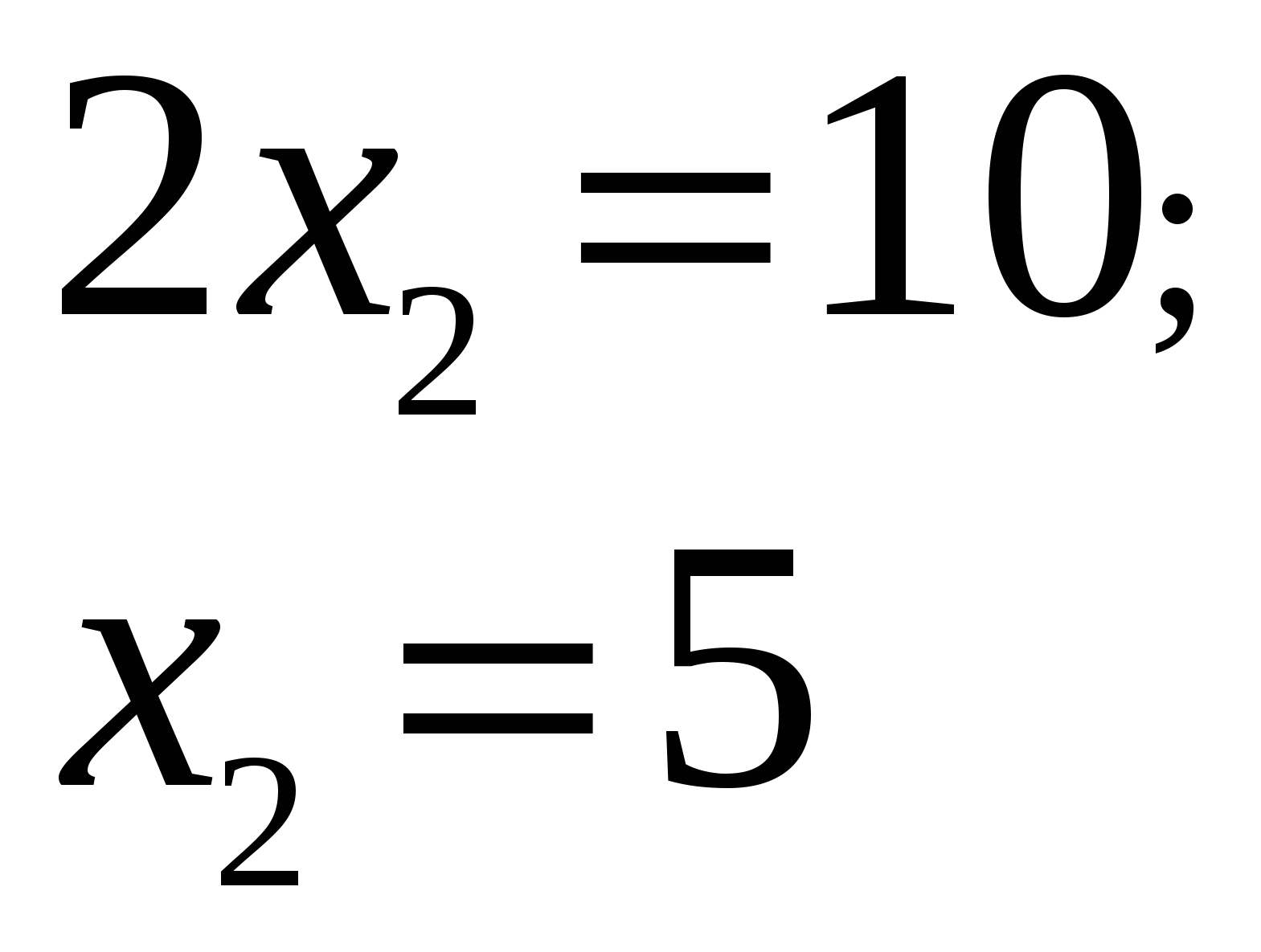 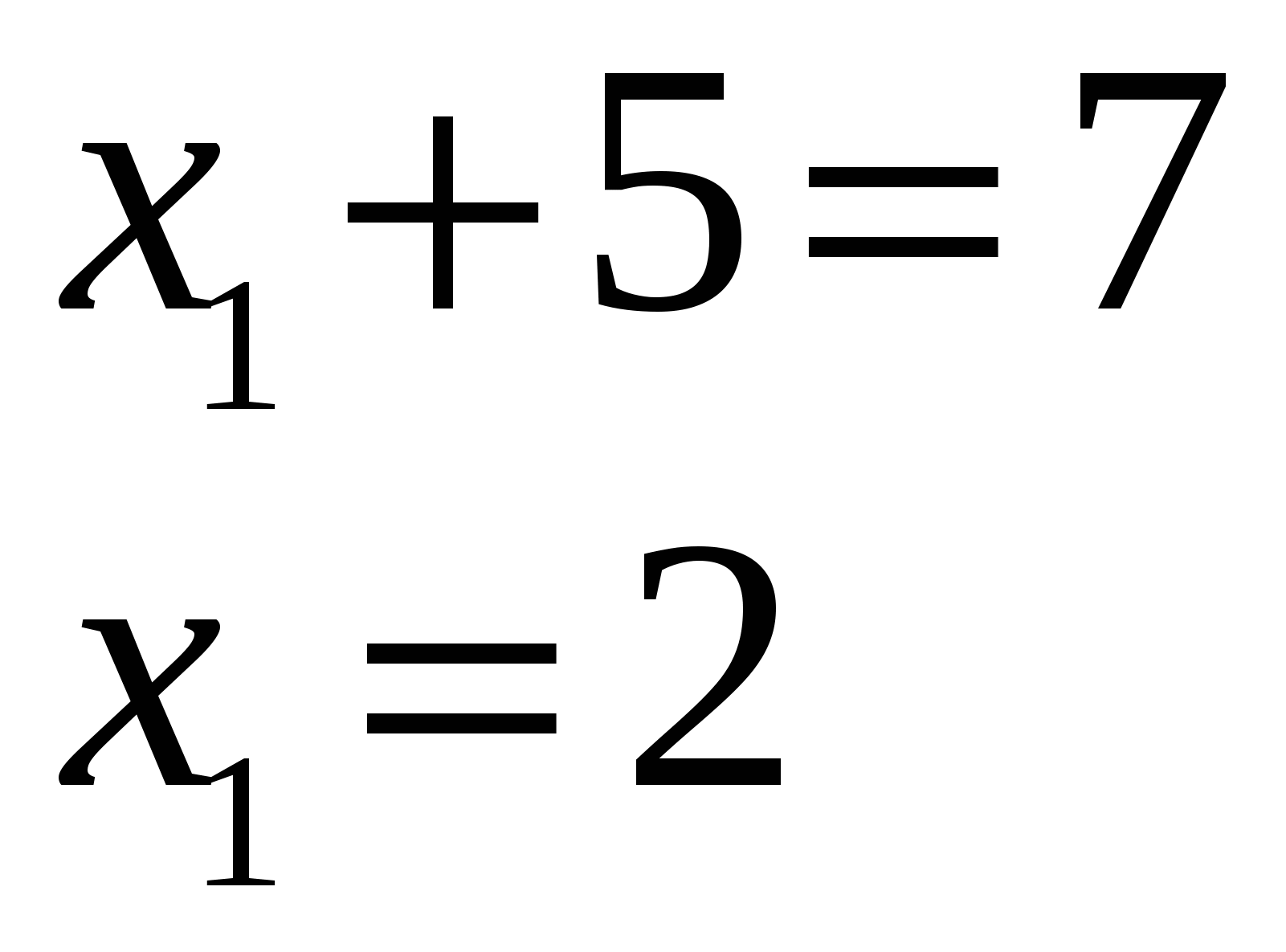
В (2;5),т.е. графическое нахождение точки В (2;5) и аналитическое решение уравнений прямых АВ и ВС – совпадают.
Если внимательно посмотрим на рисунок 1 (рис.1), то можем сделать вывод, что ″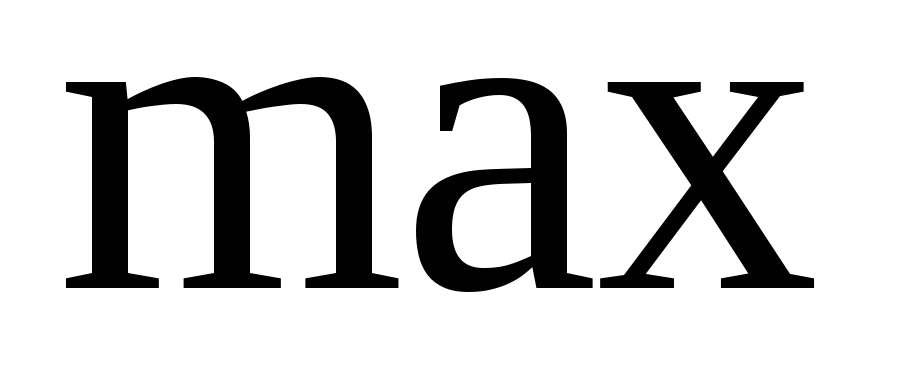 ″ значение целевой функции ″ значение целевой функции 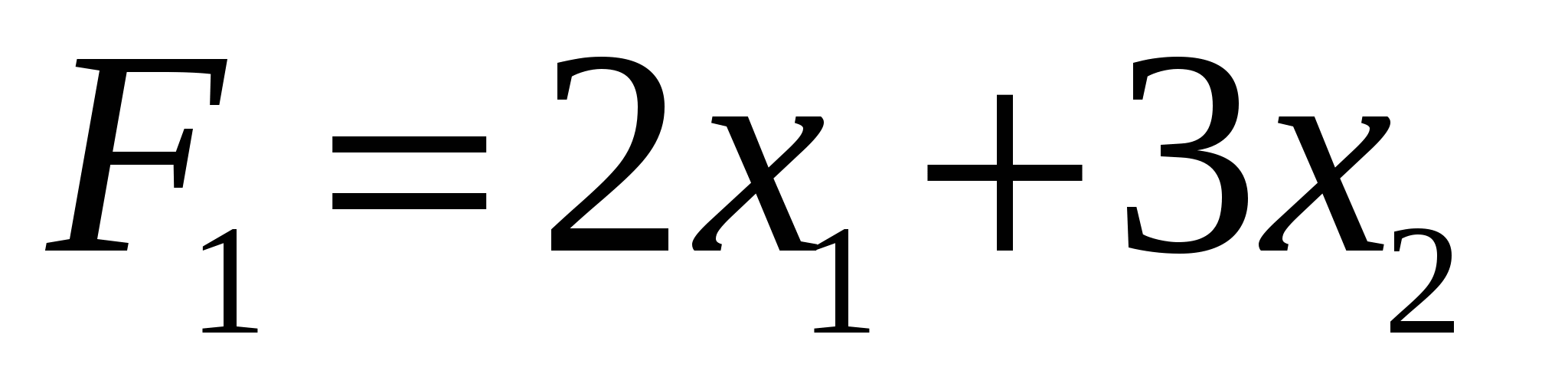 будет в т.В (2;5), так как значение будет в т.В (2;5), так как значение 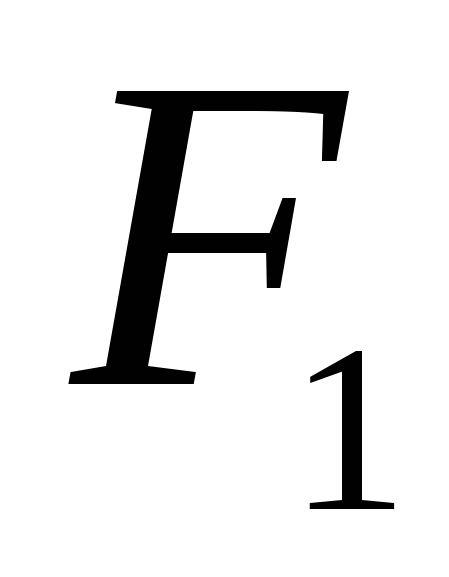 на отрезках АВ и ВС в сторону точки А и в сторону точки С уменьшаются. на отрезках АВ и ВС в сторону точки А и в сторону точки С уменьшаются.
Поэтому в нашей задаче ″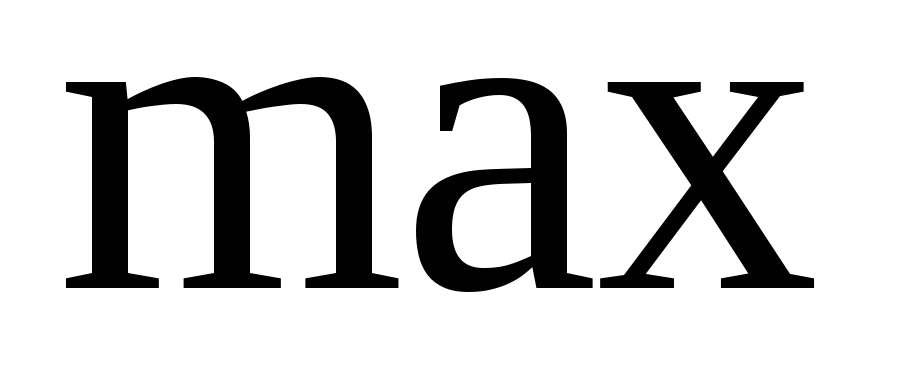 ″ значение функции ″ значение функции 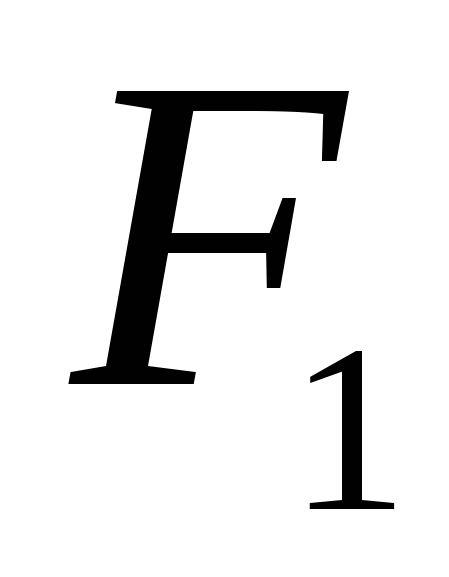 будет на границе выпуклого многоугольника АВСDEF (ОДЗ), в точке В (2;5) и будет равно: будет на границе выпуклого многоугольника АВСDEF (ОДЗ), в точке В (2;5) и будет равно:

В(2;5);
вставить рисунок 1.
б) Решить задачу линейного программирования графическим методом.


Решение:
Строится многоугольная область допустимых значений на плоскости
 (рис.2). (рис.2).


I-прямая

II –прямая

III –прямая

IV –прямая

Заштрихуем общую область допустимых значений (ABCDEF).
2. Приравняем целевую функцию
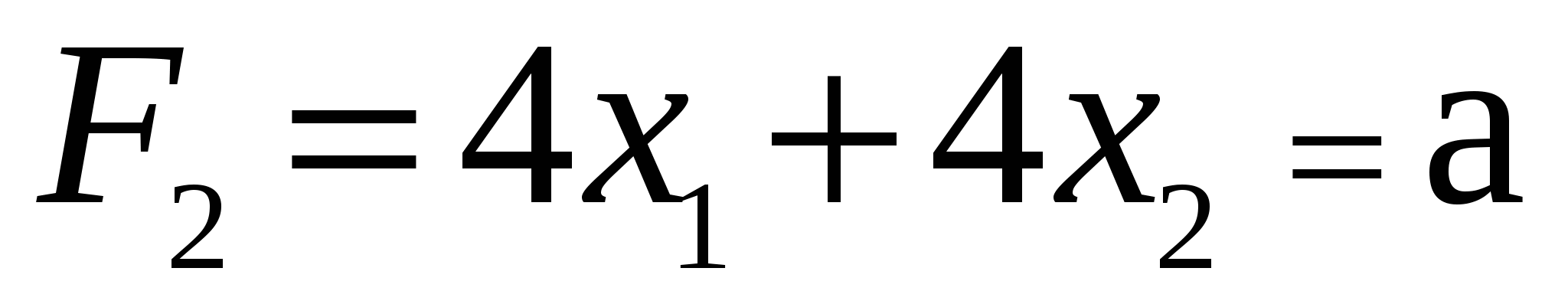
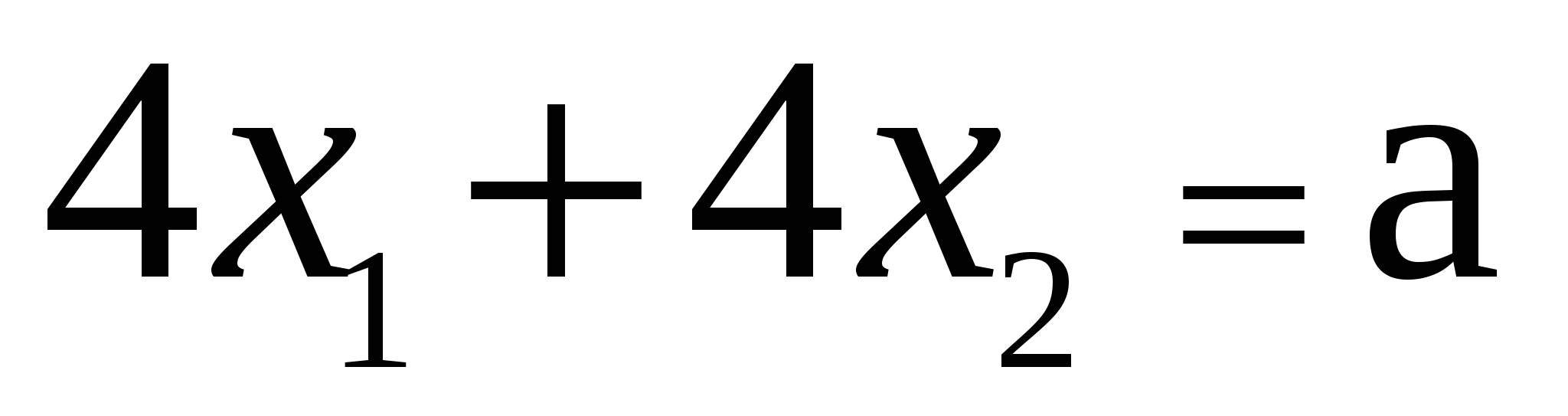 - уравнение линий уровня. - уравнение линий уровня.
Меняя значение  , получим семейство параллельных прямых, каждая из которых называется линией уровня. , получим семейство параллельных прямых, каждая из которых называется линией уровня.
Пусть 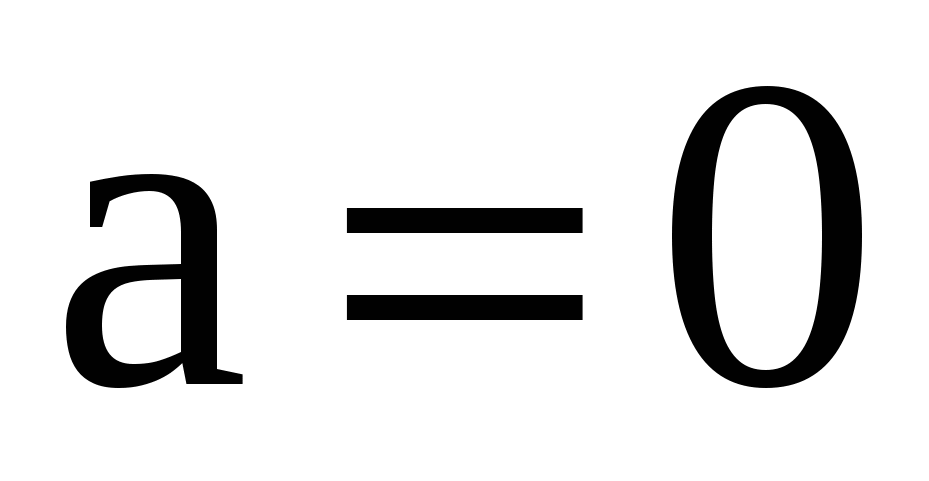

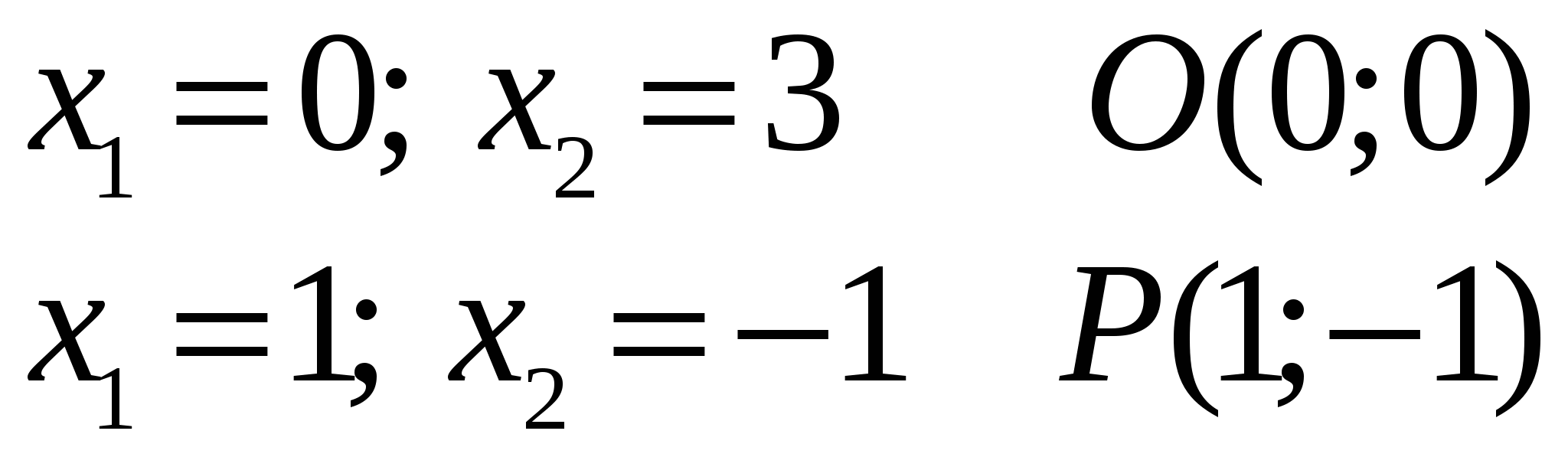
Линия уровня  перпендикулярная вектору перпендикулярная вектору  передвигается ‖-но самой себе в направлении вектора-градиента, в случае задачи на ″ передвигается ‖-но самой себе в направлении вектора-градиента, в случае задачи на ″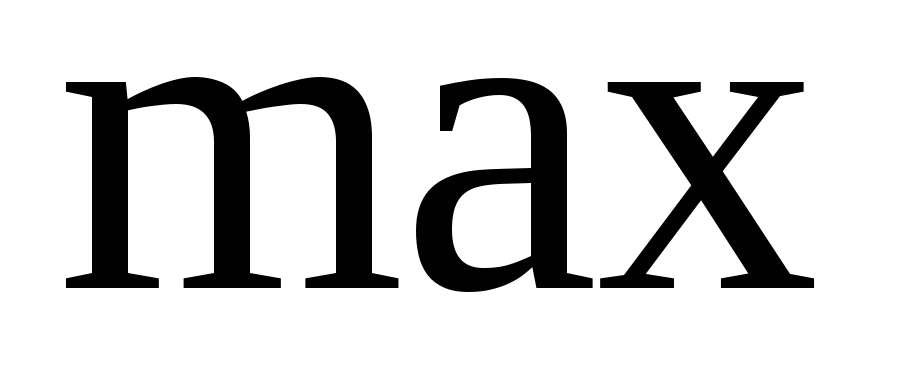 ″ до тех пор, пока линия уровня не покинет ОДЗ (многоугольник (ABCDEF)). ″ до тех пор, пока линия уровня не покинет ОДЗ (многоугольник (ABCDEF)).
Предельная точка (или точки) области являются оптимальными.
Градиент-вектор  целевой функции целевой функции  имеет координаты: имеет координаты:

Чтобы построить вектор-градиент  нужно соединить две точки. нужно соединить две точки.
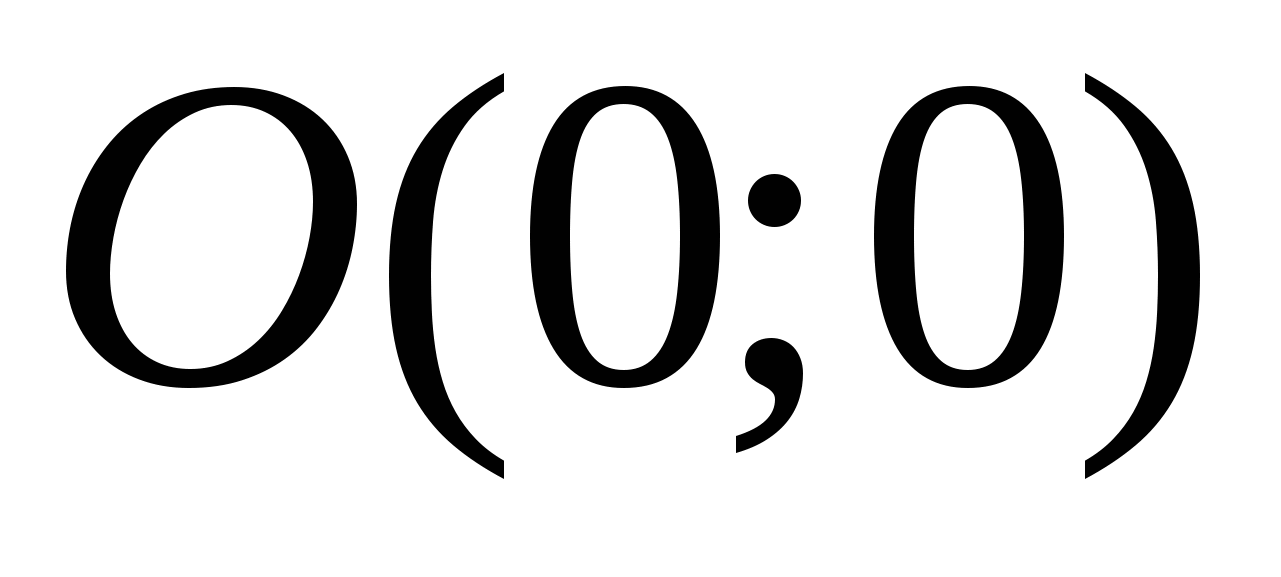 и и 
Уравнение 
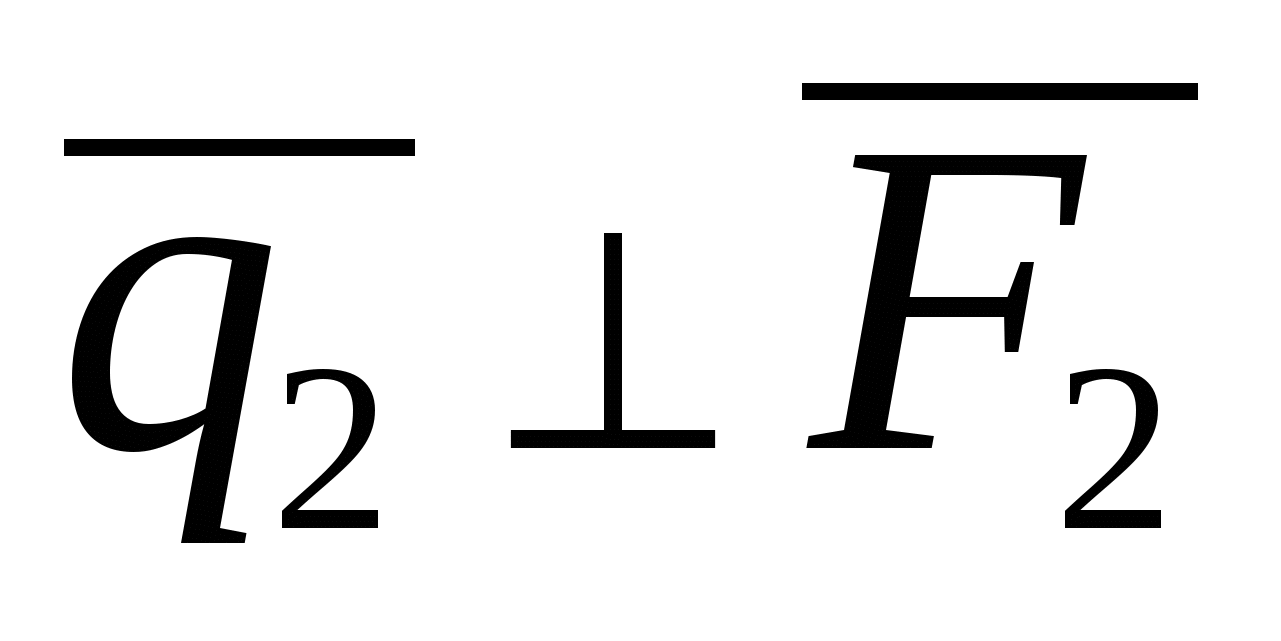
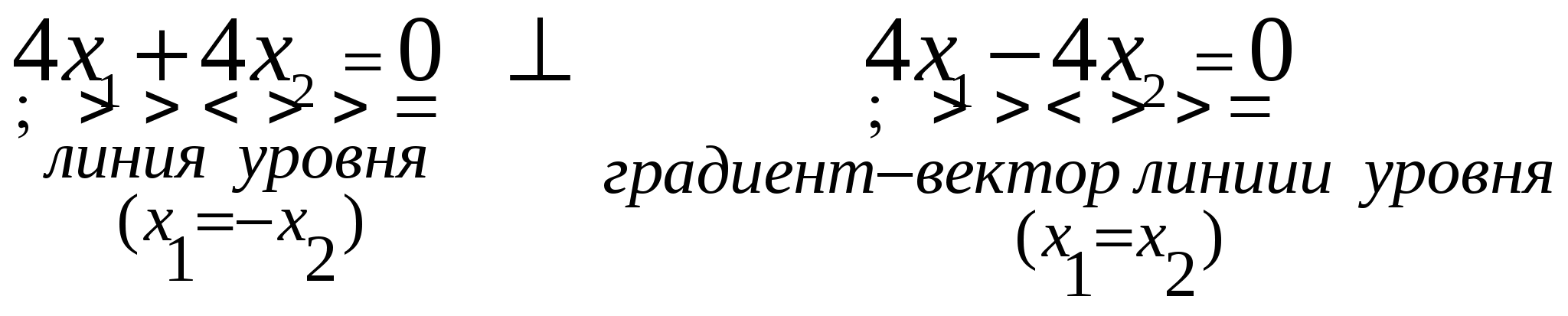
 - коэффициенты угловые. - коэффициенты угловые.
Геометрическое решение задачи показано на рис.2. Из него следует, что линии уровня с максимальным уровнем совпадают с граничной линией ВС области допустимых решений (ABCDEF), т.е. с линией  . .
Дана ситуация возможна только в том случае, если коэффициенты целевой функции пропорциональны коэффициентам какой-либо прямой ограничений. Следовательно, на всем отрезке ВС целевая функция  принимает одно и тоже оптимальное значение. принимает одно и тоже оптимальное значение.
Это означает, что задача имеет бесконечное множества оптимальных решений (их задают координаты отрезка ВС ( ) среди которых базисных оптимальных решений два- соответственно в угловых точках В(2,5) и С(5,5 ; 1,5). ) среди которых базисных оптимальных решений два- соответственно в угловых точках В(2,5) и С(5,5 ; 1,5).
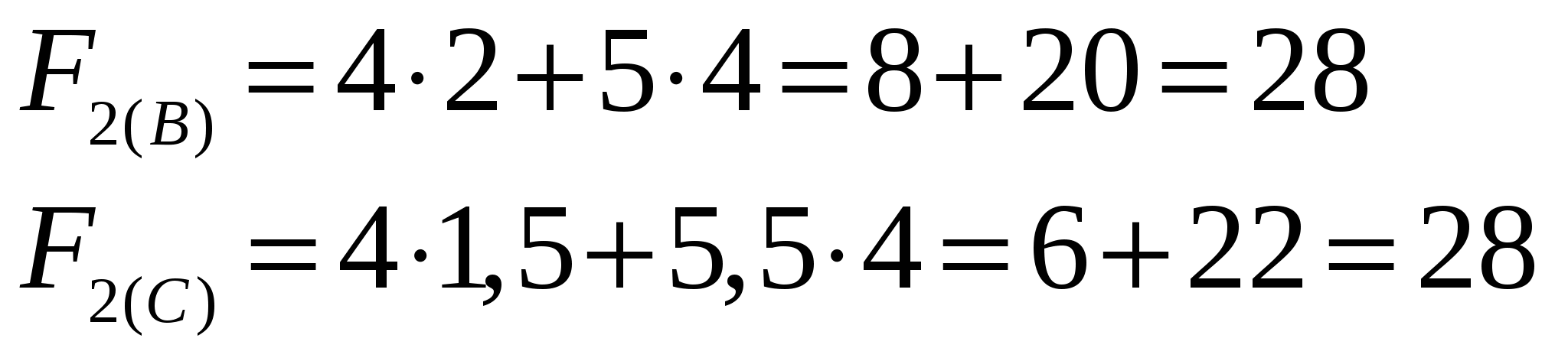
Максимальное значение целевой функции  можно найти, подставив координаты любой точки отрезка ВС в уравнение целевой функции можно найти, подставив координаты любой точки отрезка ВС в уравнение целевой функции  . .
вставить рисунок 2.
№4.
Запас груза 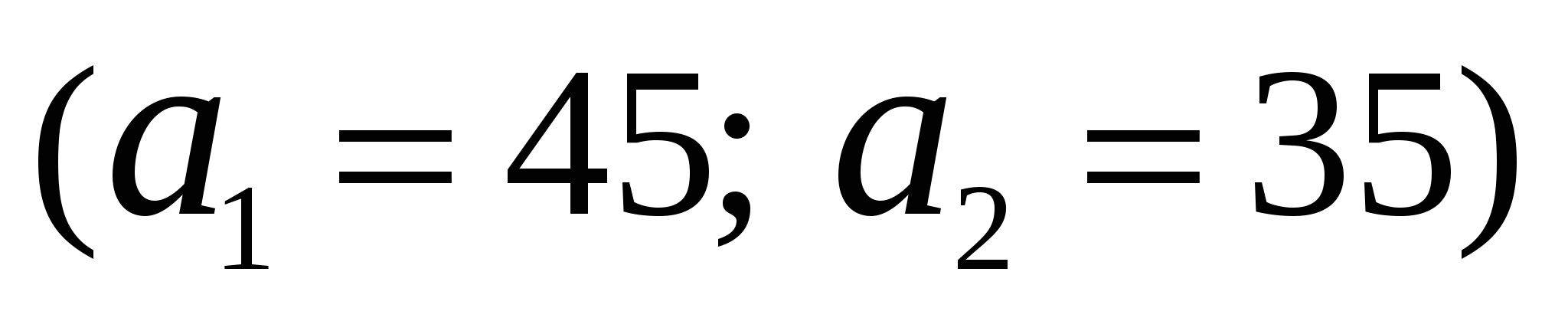 . .
Потребности в пункте назначения в грузе  . .
Матрица транспортных расходов  . .
Целевая функция:

Условие:
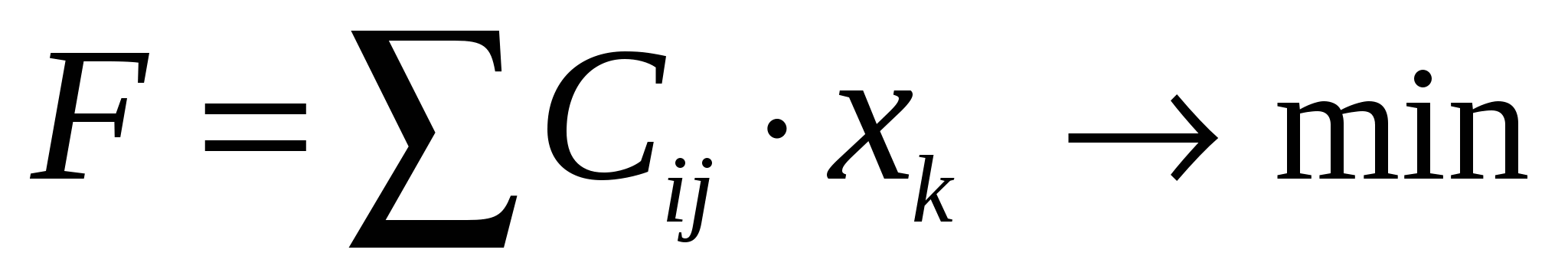
 ‒ д.стоимость удовлетворять ограничениям по запасам и потребностям и ‒ д.стоимость удовлетворять ограничениям по запасам и потребностям и 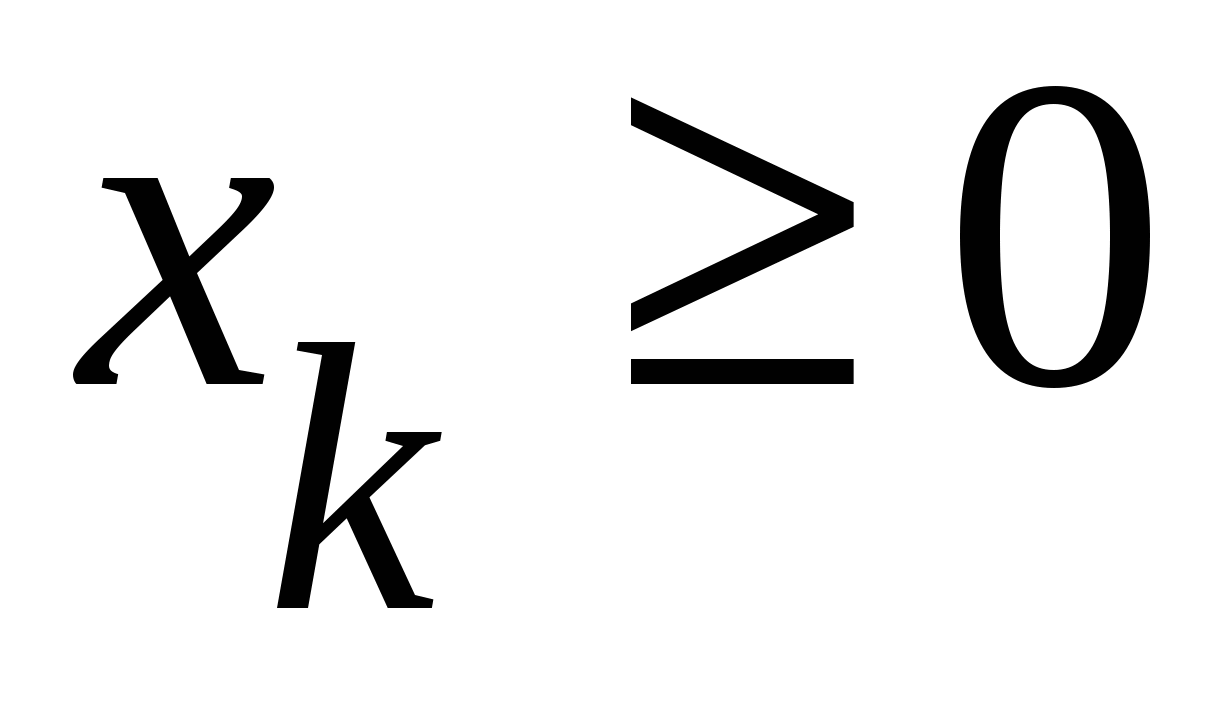 . .

Транспортная задача разрешима, если соблюдем условие баланса.

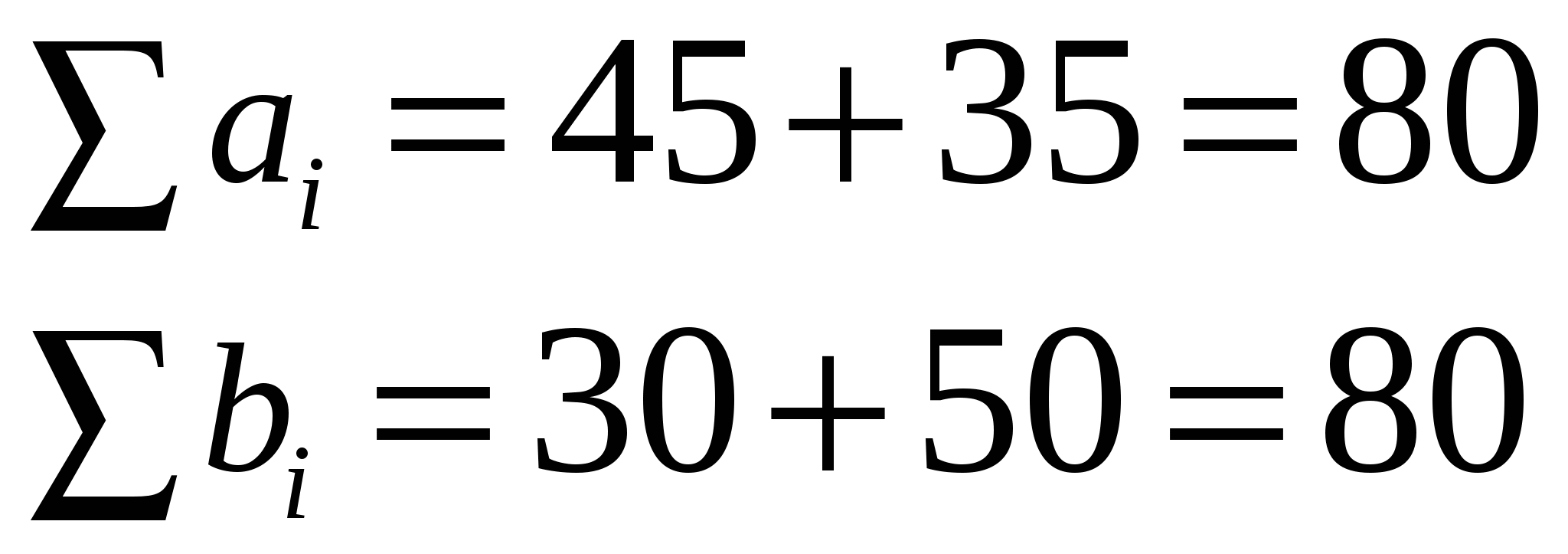
Следовательно, задача является закрытой (сбалансированной).
Приведем систему ограничений к виду (введем в каждое условие искусственную переменную  ). ).
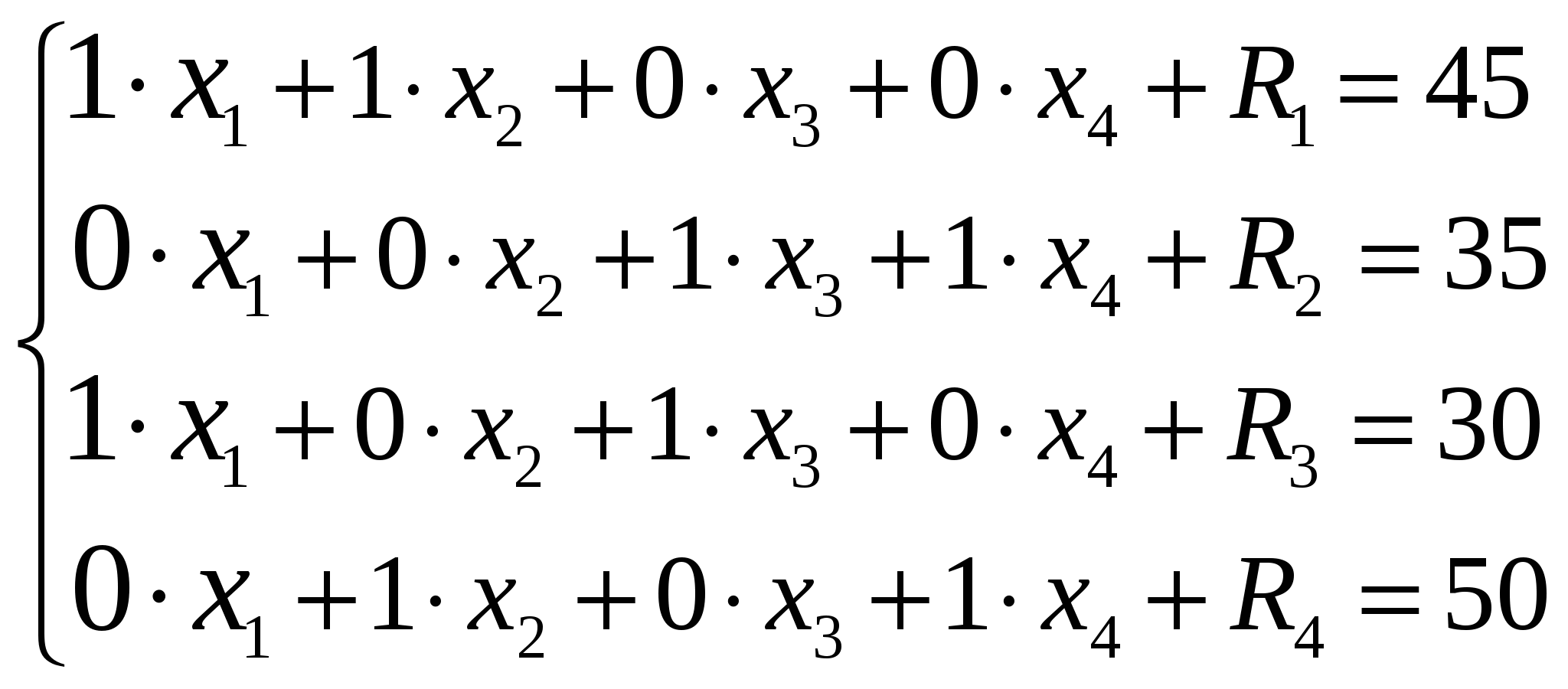
Переходим к формированию исходной симплекс-таблицы.
В строку  заносятся коэффициенты целевой функции. заносятся коэффициенты целевой функции.
Строка М ‒ элементы рассчитываются как сумма соответствующих условий равенств (тех, которые после приведения к каноническому виду содержат переменные  ), взятых с противоположным знаком. ), взятых с противоположным знаком.
|

|

|
|

|
Свободные члены
|

|
3
|
4
|
5
|
2
|
0
|

|
1
|
1
|
0
|
0
|
45
|
|
0
|
0
|
1
|
1
|
35
|

|
1
|
0
|
1
|
0
|
30
|

|
0
|
1
|
0
|
1
|
50
|
М
|
-2
|
-2
|
-2
|
-2
|
160
| |
 Скачать 0.86 Mb.
Скачать 0.86 Mb.