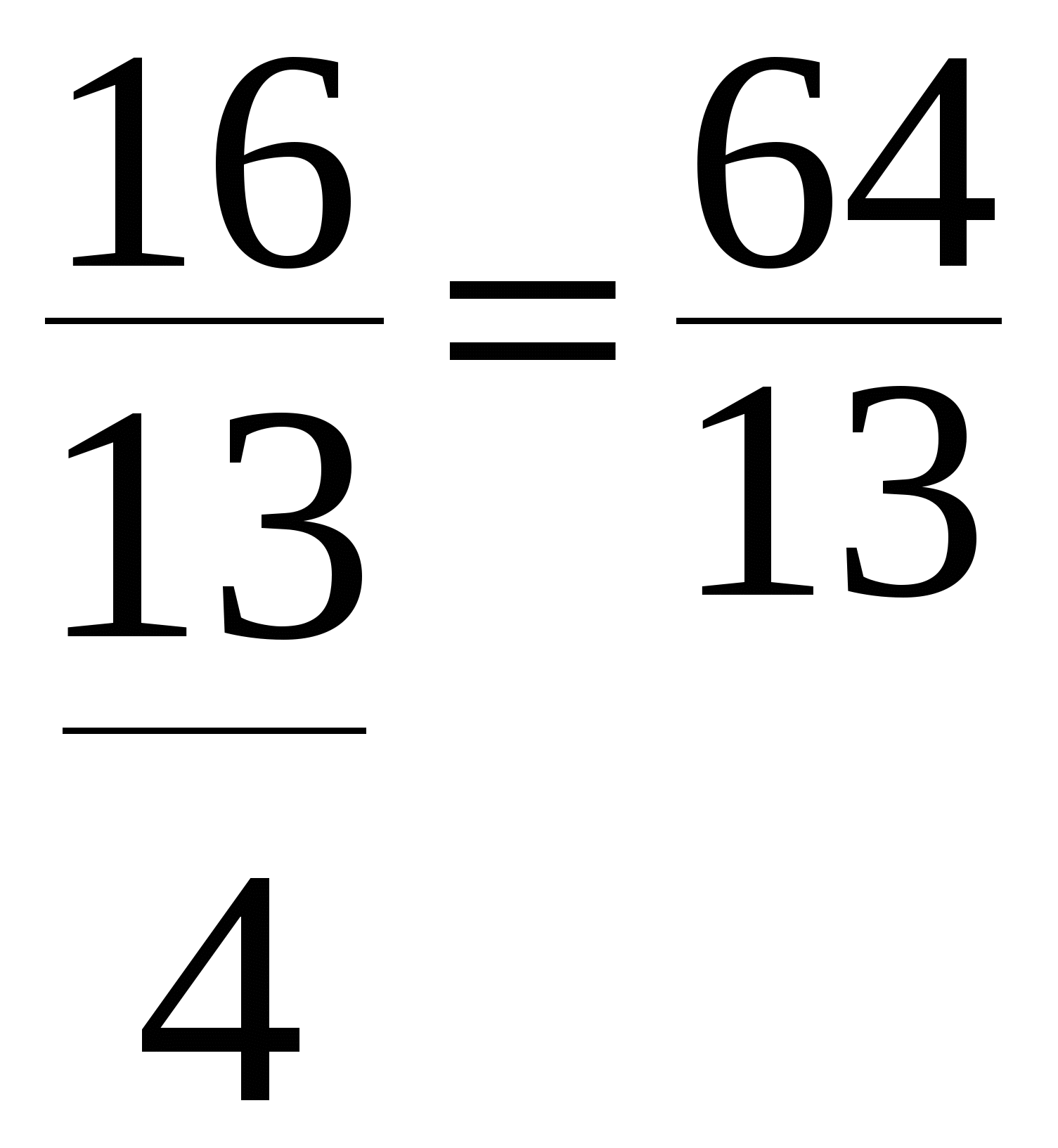Линейная алгебра. Решение Строится многоугольная область допустимых значений на плоскости (рис. 1)

• Название: Решение Строится многоугольная область допустимых значений на плоскости (рис. 1)
• Дата: 03.04.2018
• Размер: 0.86 Mb.
• Имя файла: Линейная алгебра.doc
• Тип: Документы; #40227
• страница: 3 из 4

,,.



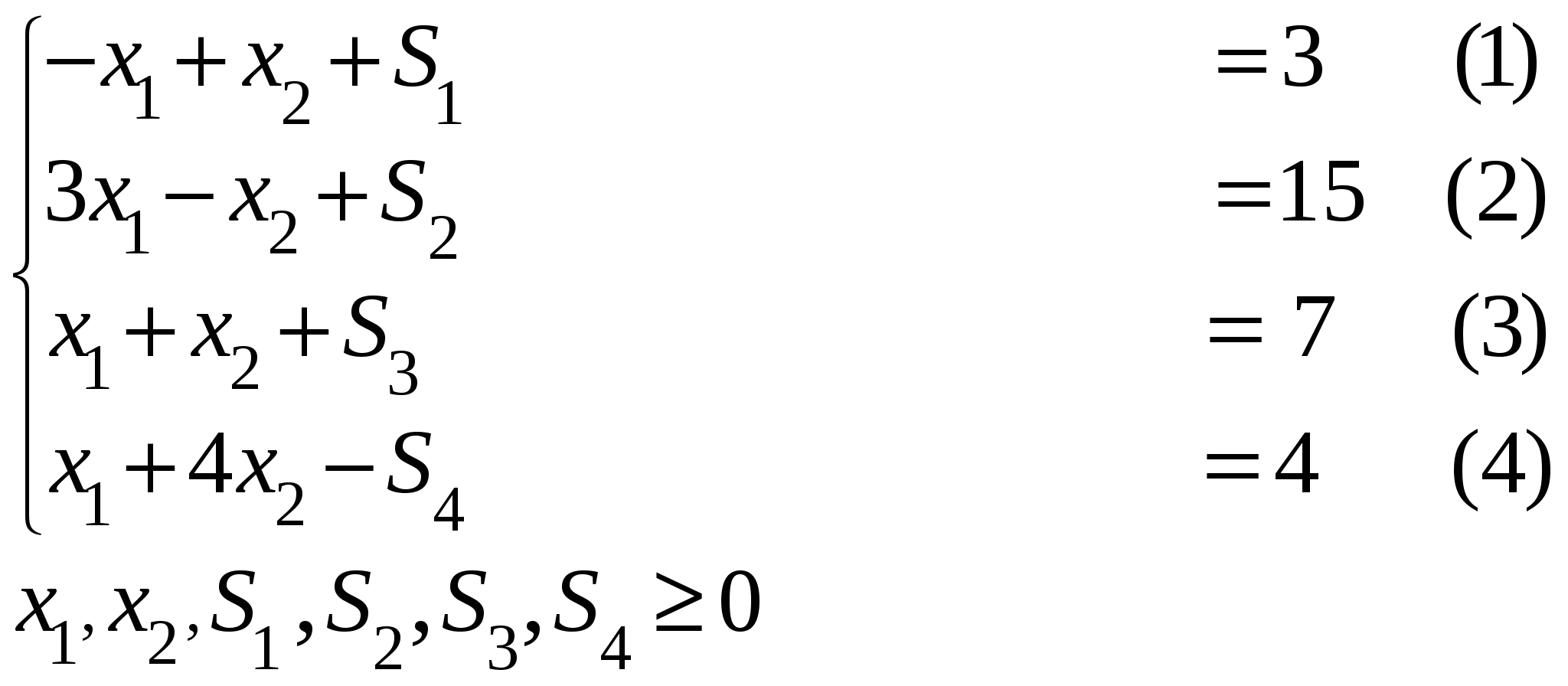Шаг 3: Ищем в системе ограниченно базисные переменные . Не все уравнения содержат базисные переменные.

Это значит, что исходная задача не содержит в себе допустимого базисного решения.

Для его нахождения вначале составим и решим вспомогательную задачу.

Введем в уравнение (4) искусственную неотрицательную переменную .

Получим: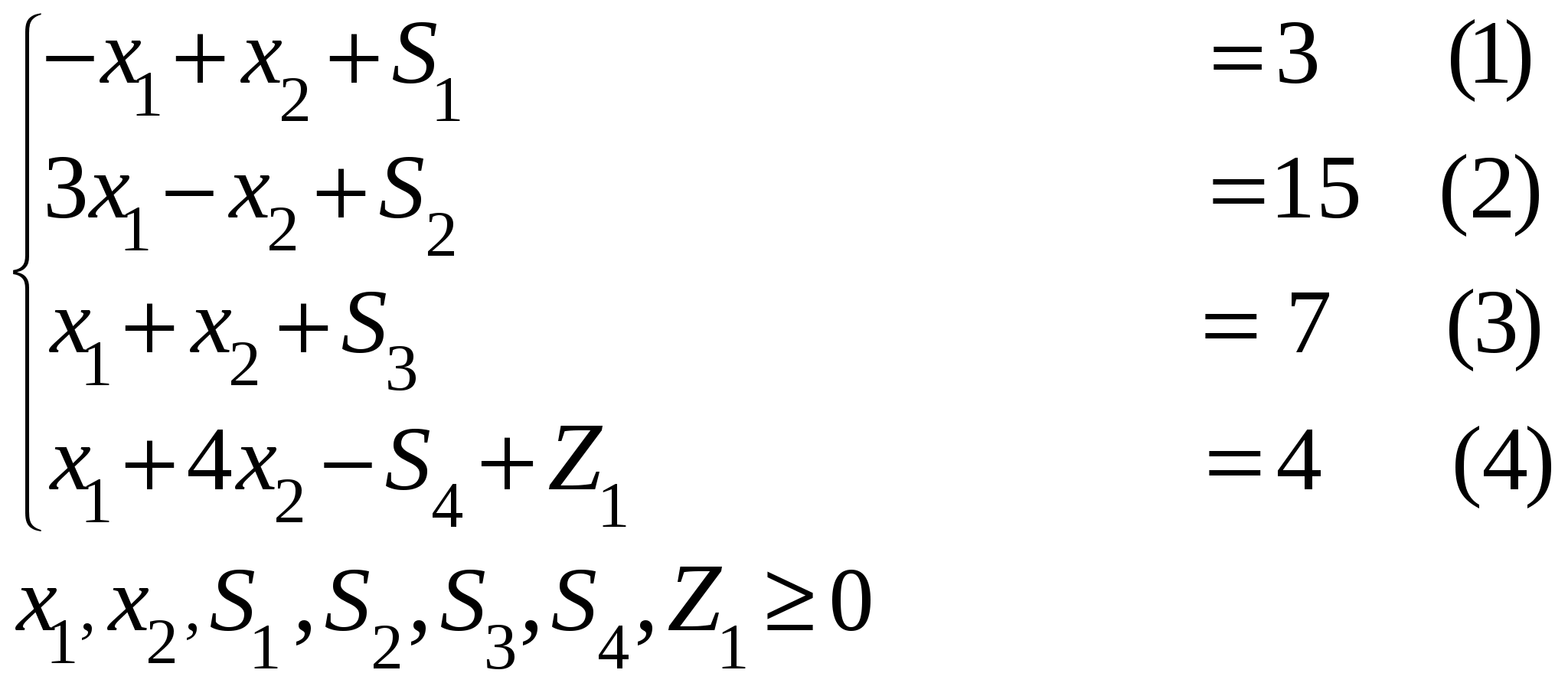



с базисными переменными .

Формируем вспомогательную целевую функцию.

и проведем ее минимизацию в заданной системе ограничений.

Для решения вспомогательной задачи симплекс-методом выразим функцию через свободные переменные , для этого вычтем из функции уравнение (4).



Теперь формируем начальную симплекс-таблицу.

Шаг 4: (начальная симплекс-таблица)

БП								Решение	Отношение
	-1	1	1	0	0	0	0	3
	3	-1	0	1	0	0	0	15	−
	1	1	0	0	1	0	0	7
	1	1	0	0	0	-1	1	4
	4	4	0	0	0	0	0	0	−
	-1	-4	0	0	0	1	0	-4	−

Интерация Отношения

БП							Решение	Отношение
		0	1	0	0		2	−
		0	0	1	0		16
		0	0	0	1		6
		1	0	0	0		1
	3	0	0	0	0	1	-4	−
	0	0	0	0	0	0	0	−

Получено оптимальное решение вспомогательной задачи (найдем функции , т.к. в строке целевой функции нет отрицательных коэффициентов. Строка нам больше не нужна.

Интерация1

БП							Решение	Отношение
		0	1	0	0		2	−
		0	0	1	0		16
		0	0	0	1		6
		1	0	0	0		1
	3	0	0	0	0	1	-4	−

Интерация 2

БП							Решение	Отношение
	0	5	1	0	0	-1	7	−
	0	-13	0	1	0	3	3
	0	-3	0	0	1	1	3
	1	4	0	0	0	-1	4	−
	0	-12	0	0	0	4	-16	−