Линейная алгебра. Решение Строится многоугольная область допустимых значений на плоскости (рис. 1)

• Название: Решение Строится многоугольная область допустимых значений на плоскости (рис. 1)
• Дата: 03.04.2018
• Размер: 0.86 Mb.
• Имя файла: Линейная алгебра.doc
• Тип: Документы; #40227
• страница: 2 из 4

т.к. в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.

В строке М имеются отрицательные элементы, это означает, что полученное решение не оптимально. Определим ведущий столбец.

Для этого найдем в строке М максимальный по модулю отрицательный элемент – это (-2) - столбец . Ведущей строкой будет та, для которой положительное отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является , а ведущий элемент: 1.

				Свободные члены
	4	2	2	-90
	1	-1	0	15
	0	1	1	35
	0	1	0	30
	1	0	1	50
М	-2	0	-2	-100

В строке М имеются отрицательные элементы. Полученное решение, поэтому не оптимально. Далее проводим итерацию. Ведущая строка будет , а ведущий элемент: 1.

			Свободные члены
	-6	2	-150
	-1	0	15
	1	1	35
	1	0	30
	1	1	35
М	-2	-2	-70

В строке М имеются отрицательные элементы, это означает, что полученное решение не оптимально. Определим ведущий столбец. Это столбец . (элемент в М (-2)). Ведущей строкой является ,а ведущий элемент:1.

			Свободные члены
	-6	2	-330
	1	0	45
	-1	1	5
	1	0	30
	-1	1	5
М	2	-2	-10

Далее: ведущий столбец – столбец . Ведущей строкой является , а ведущий элемент: 1.

		Свободные члены
	-4	-340
	1	45
	-1	5
	1	30
	0	0
М	0	0

В строке имеется отрицательные элементы, значит полученное решение не оптимально.

Далее: ведущей строкой является , а ведущий элемент:1.

		Свободные члены
	4	-220
	-1	15
	1	35
	1	30
	0	0
М	0	0

Так как исходной задачей был поиск ″″, оптимальное решение есть свободный член строки , взятой с противоположным знаком. Найдено оптимальное решение: (минимальные транспортные расходы или ) при значениях переменных:

(количество продукции, доставленное со склада №1 к потребителю №2).

(количество продукции, доставленное со склада №2 к потребителю №2).

(количество продукции, доставленное со склада №1 к потребителю №1).





млн.руб.

№5.

5.1. Записать ЗЛП, двойственную к задаче линейного программирования.

1. Приводим все неравенства системы ограниченной исходной задачи к одному символу (причем в задаче на ″″ к ″″, а в задаче на ″″ к ″″).

2. Составляем расширенную матрицу , в которую включаем матрицу А, столбец свободных членов и строку переменных коэффициентов целевой функции.

3. Находим .

4. Формируем двойственную задачу на основе полученной матрицы 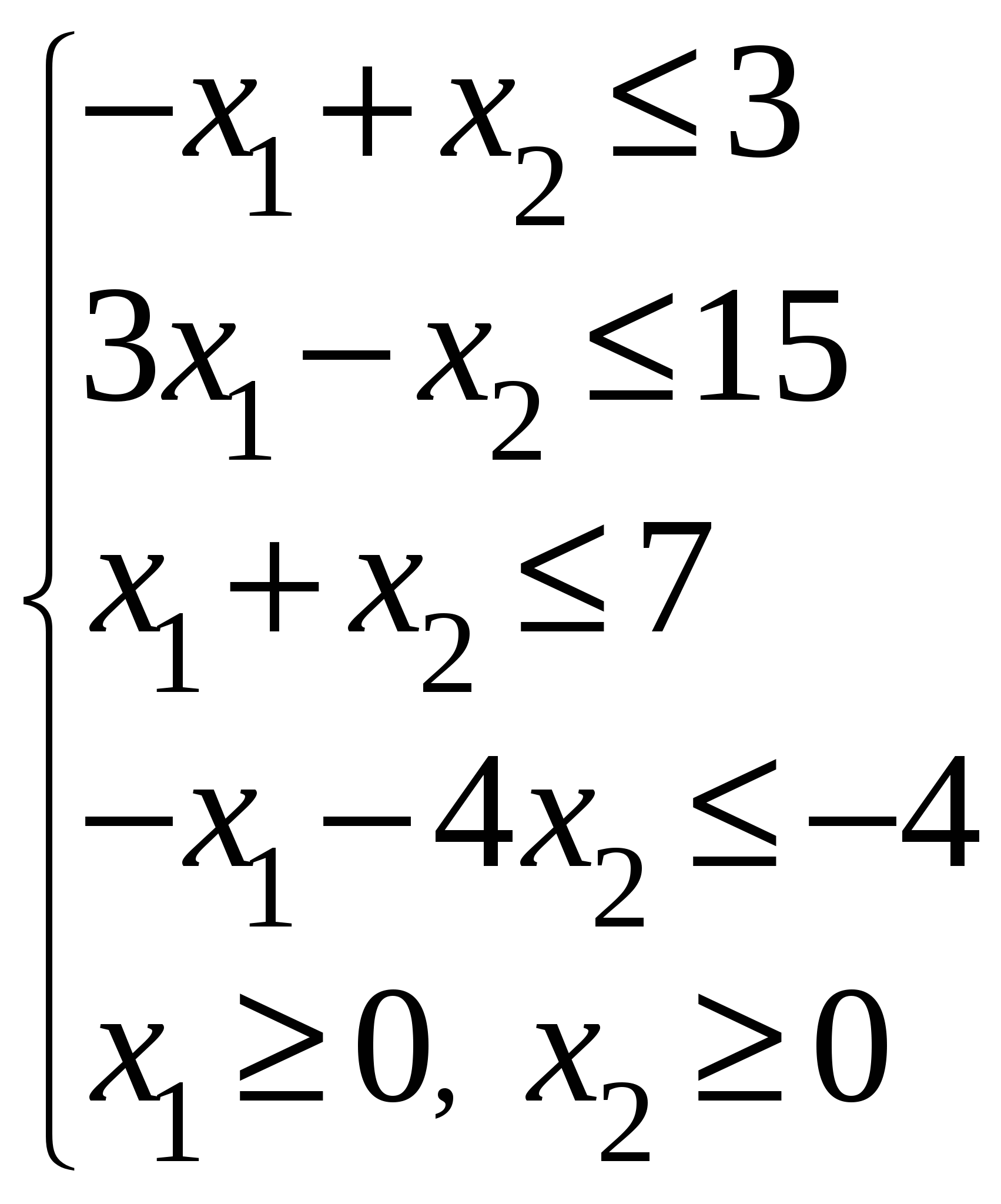и условия не отрицательности переменных.





Приведем ограничения к виду ″″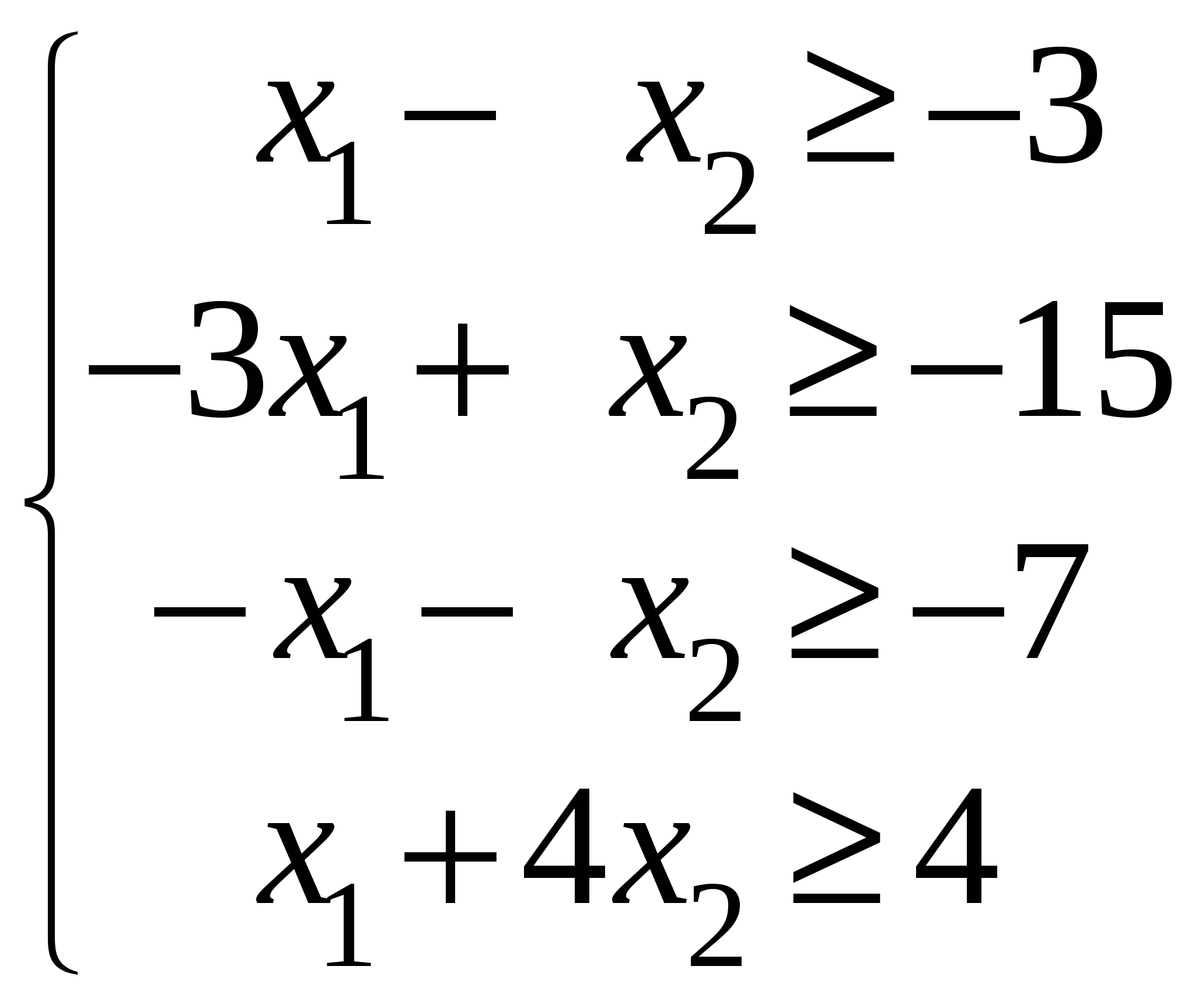



Составим расширенную матрицу .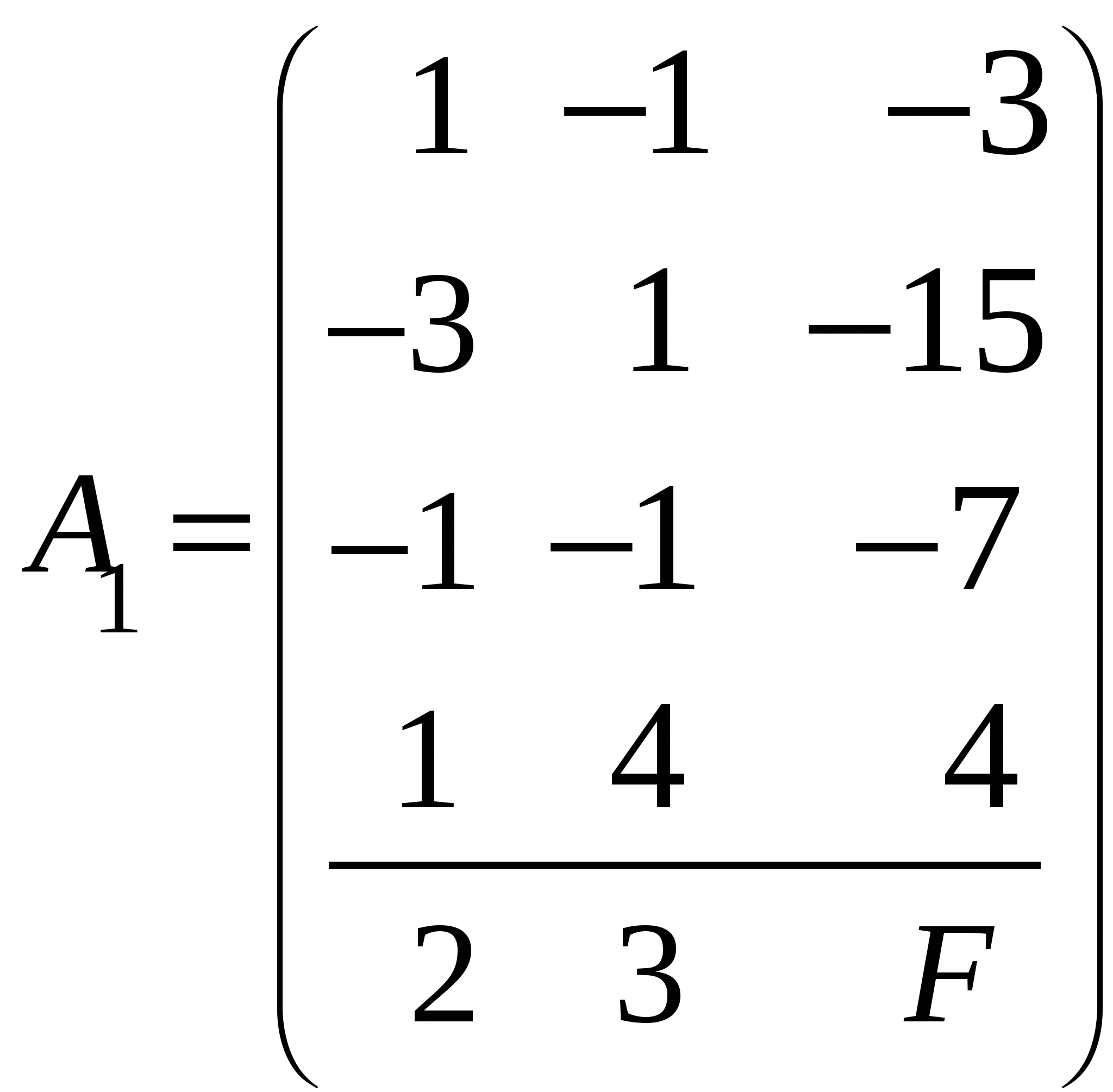



Транспортируем матрицу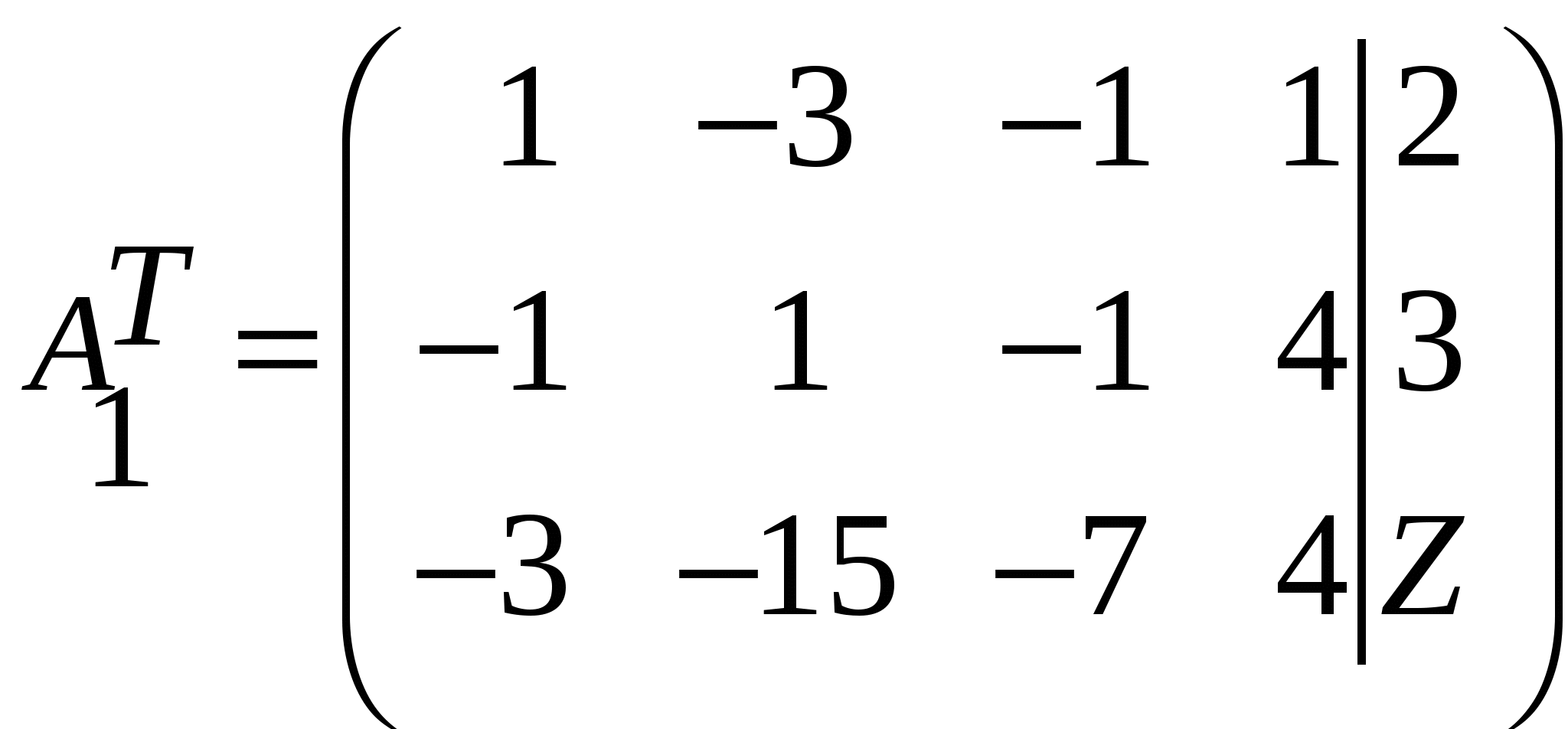



И сформируем двойственную задачу: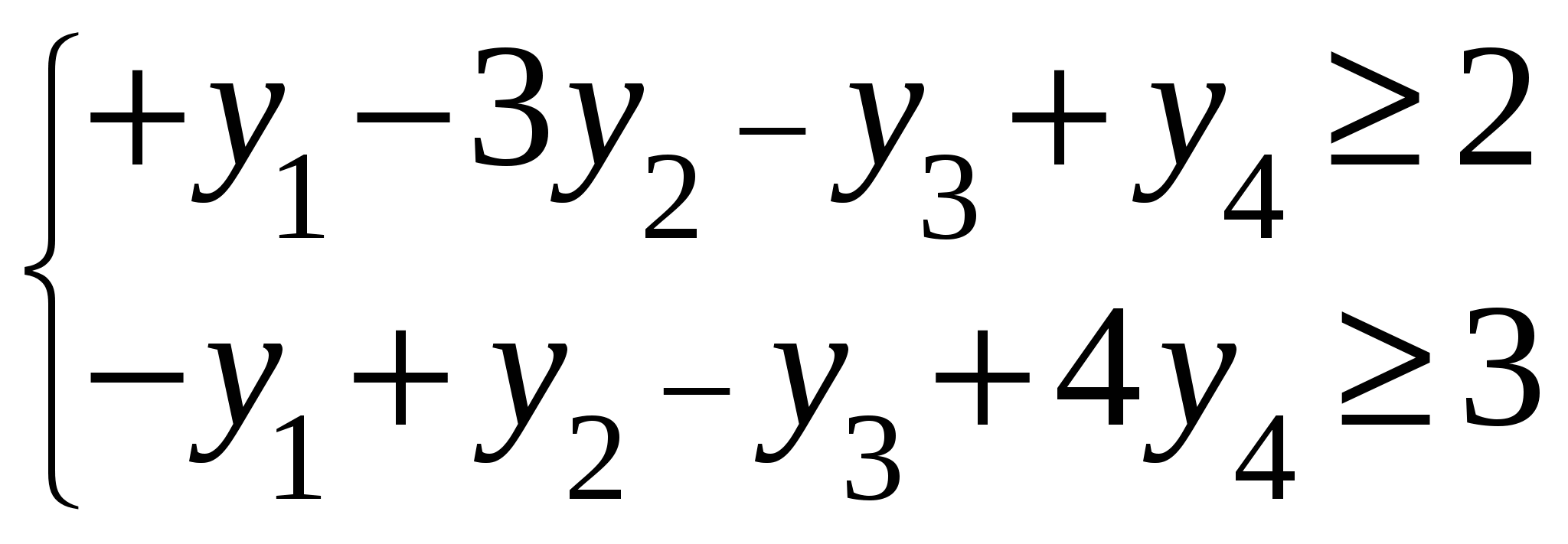





Или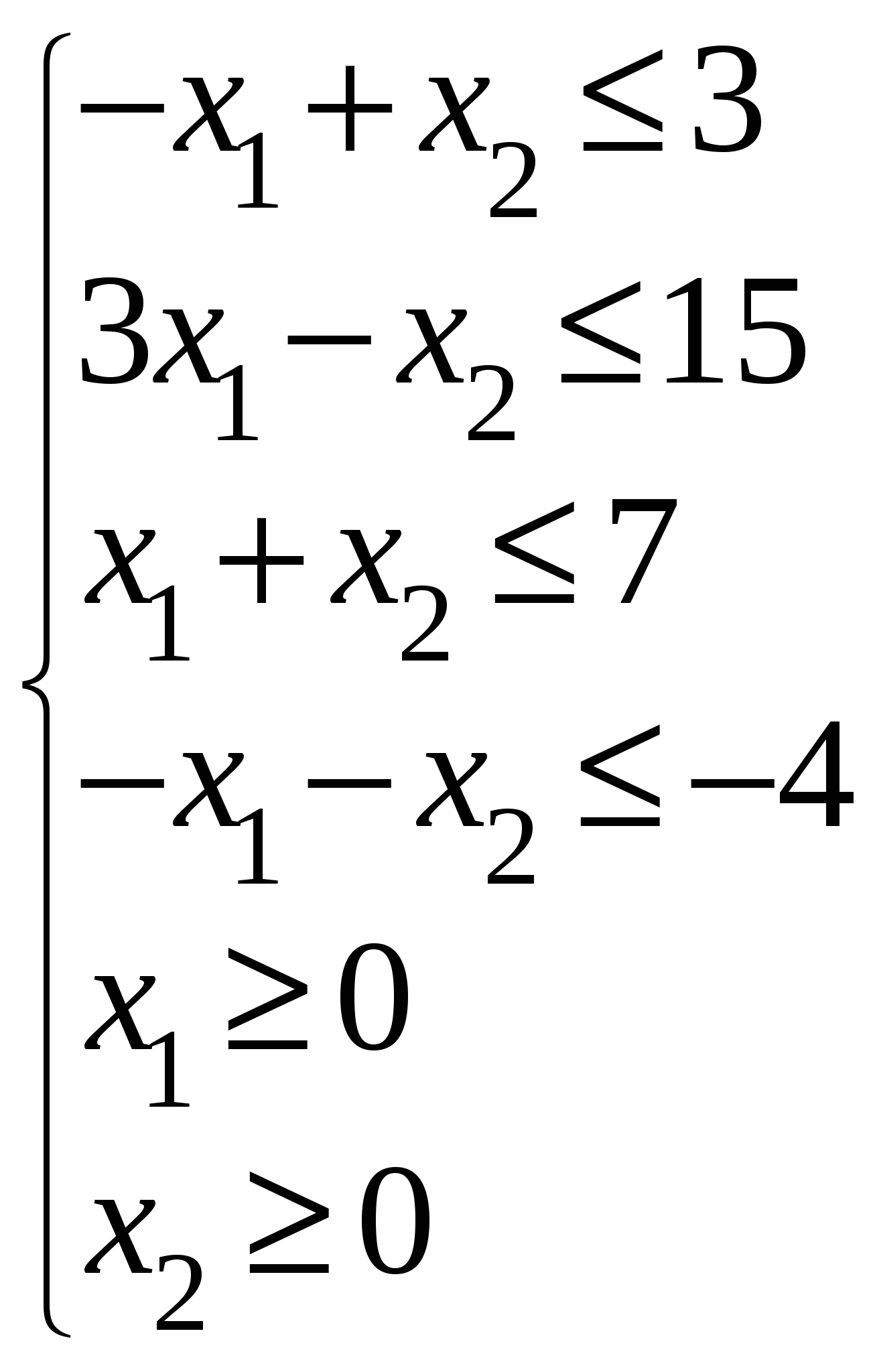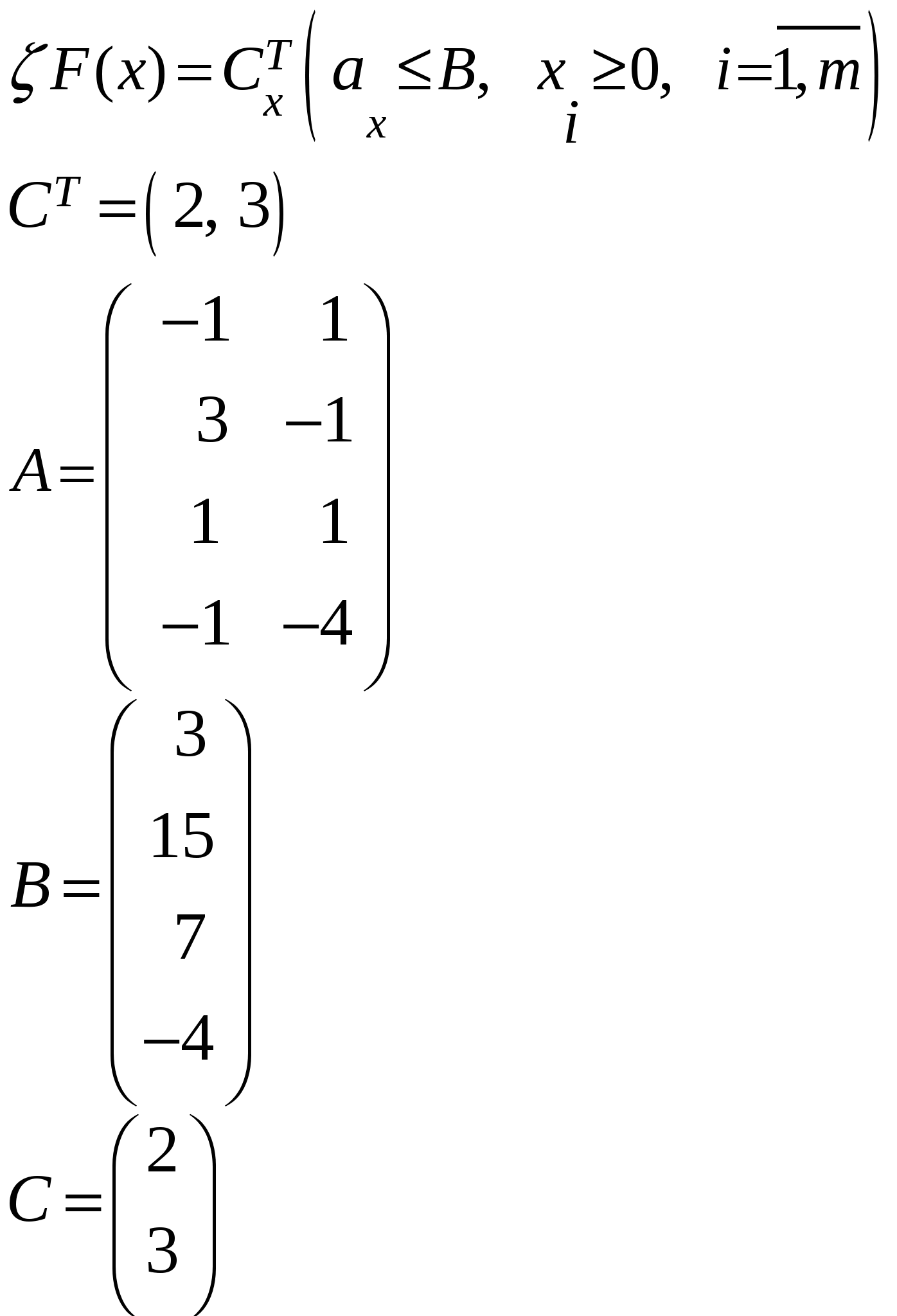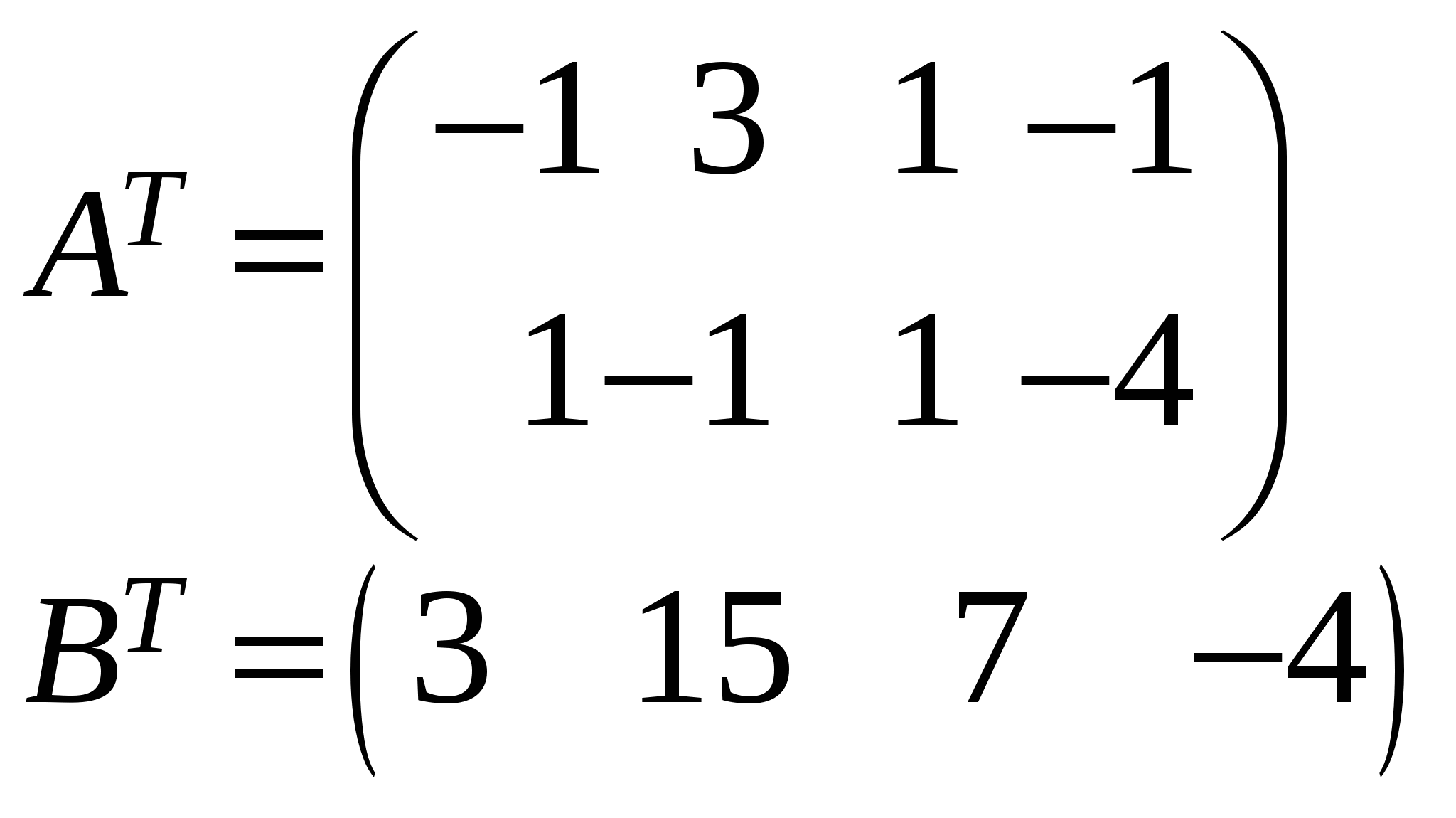







Следовательно, двойственная задача ЗЛП будет иметь вид:



Ограничения: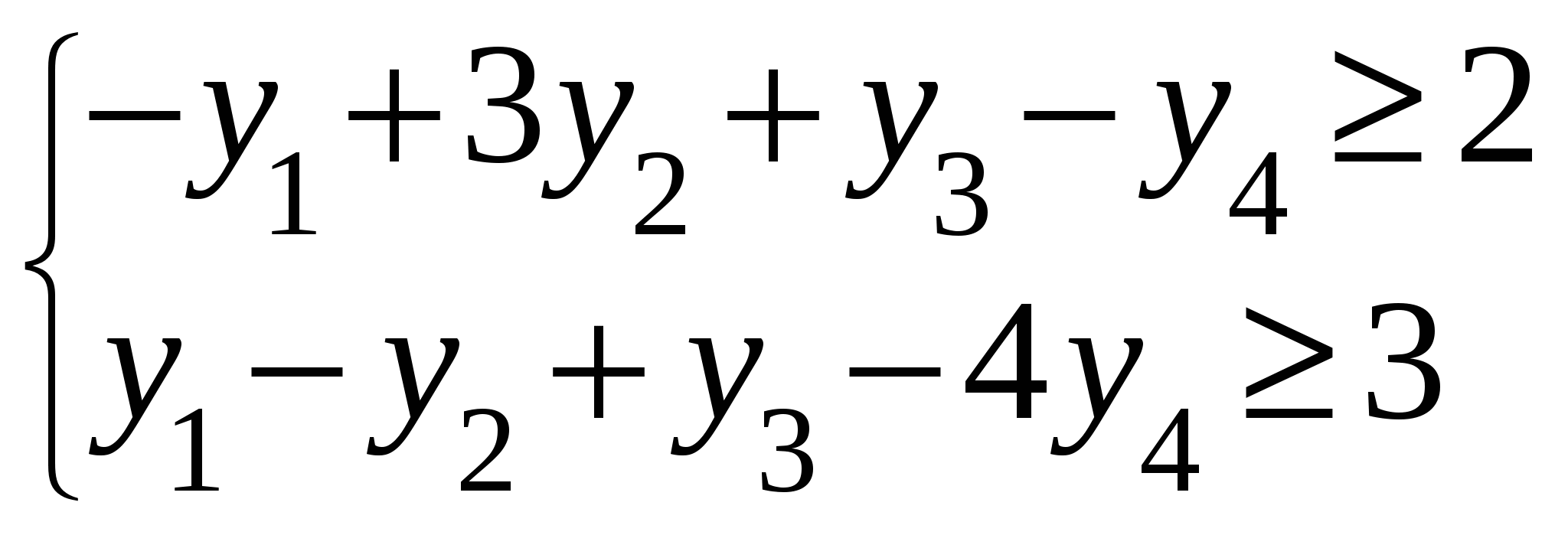



Двойственная задача исходной – эти задачи взаимно-двойственные

Наоборот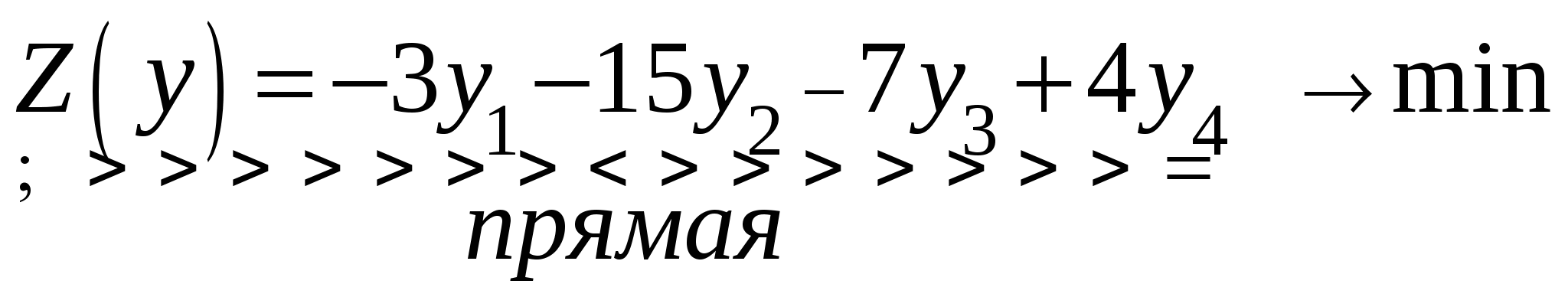



В результате получим следующие матрицы: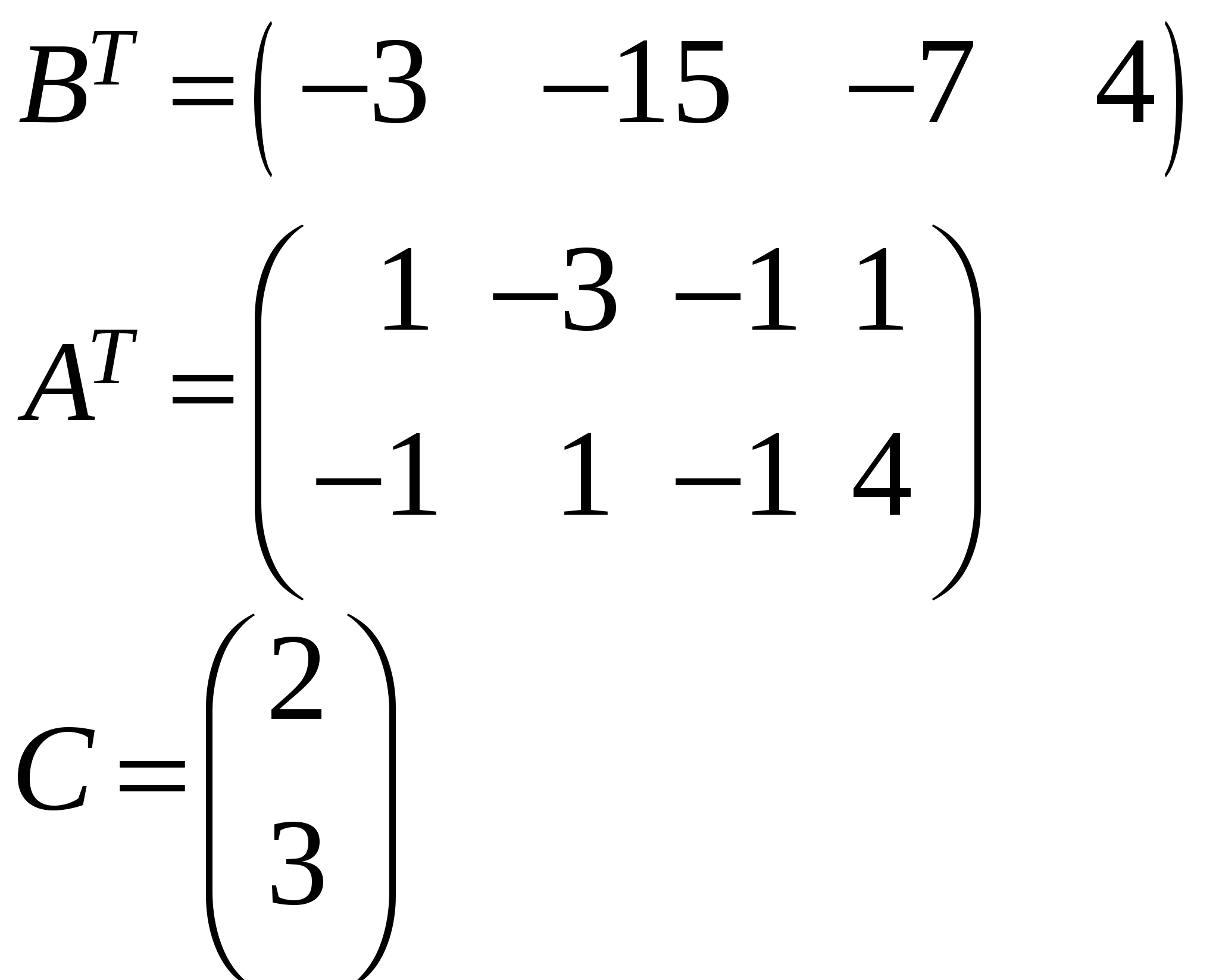



Для составления двойственной задачи: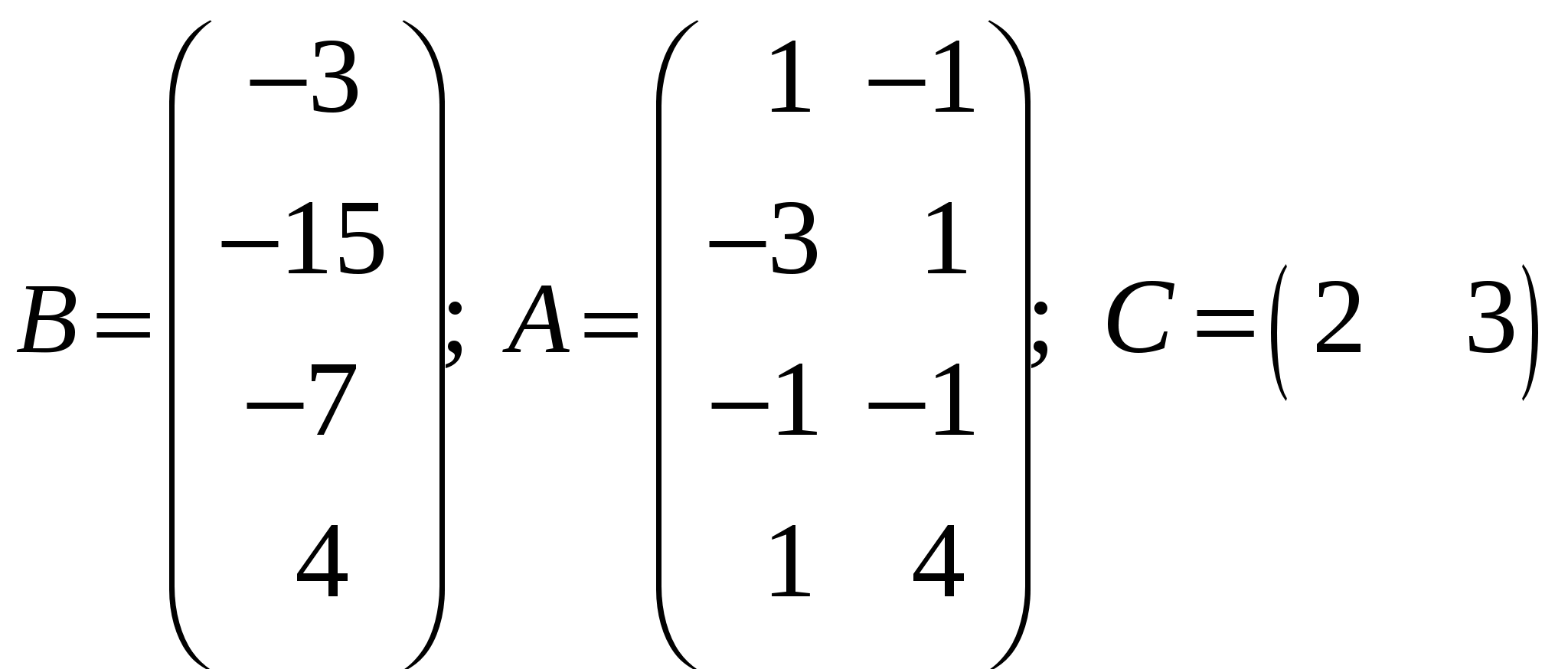



Следовательно, двойственная задача будет иметь вид:



Ограничения: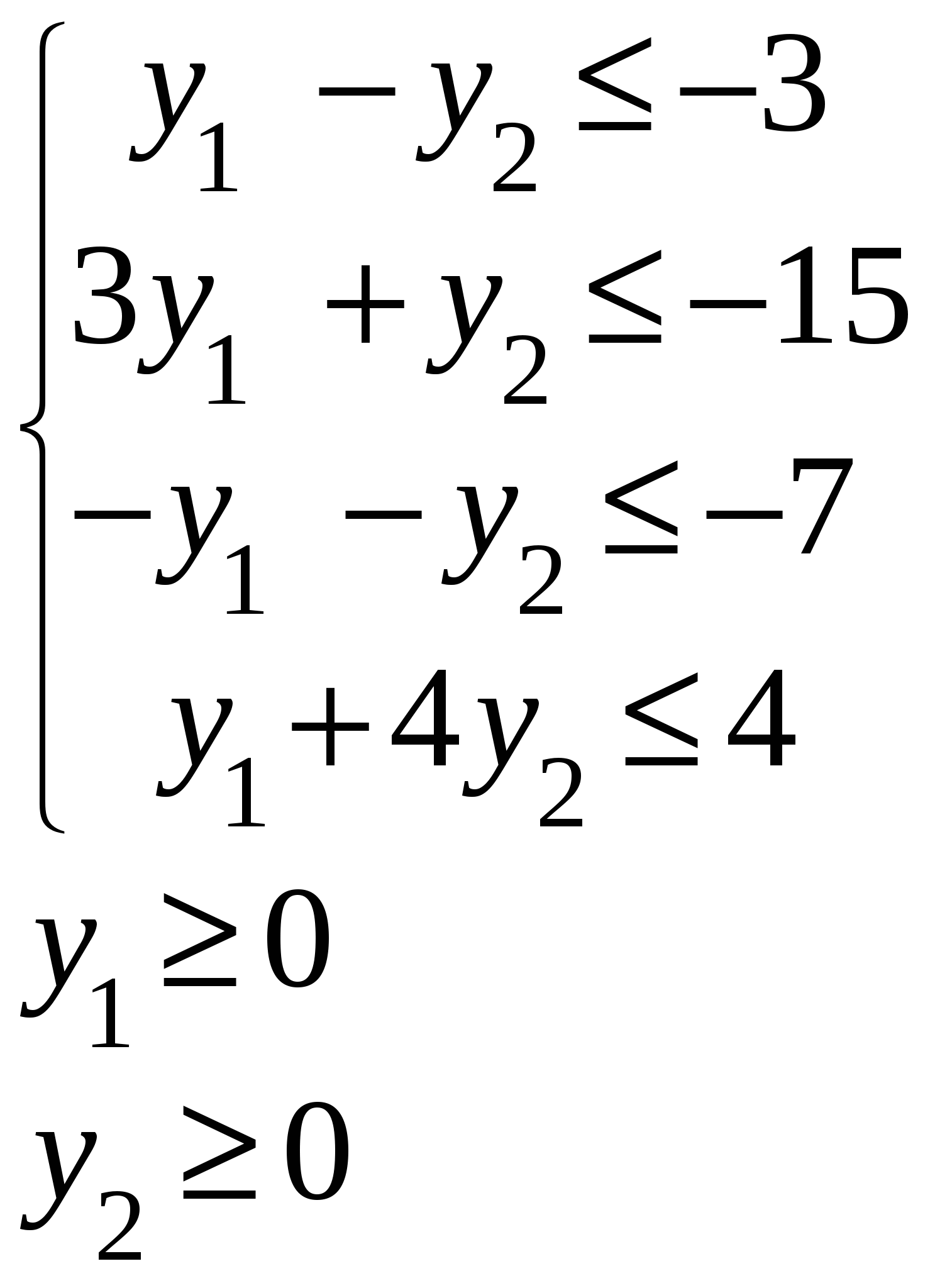



Или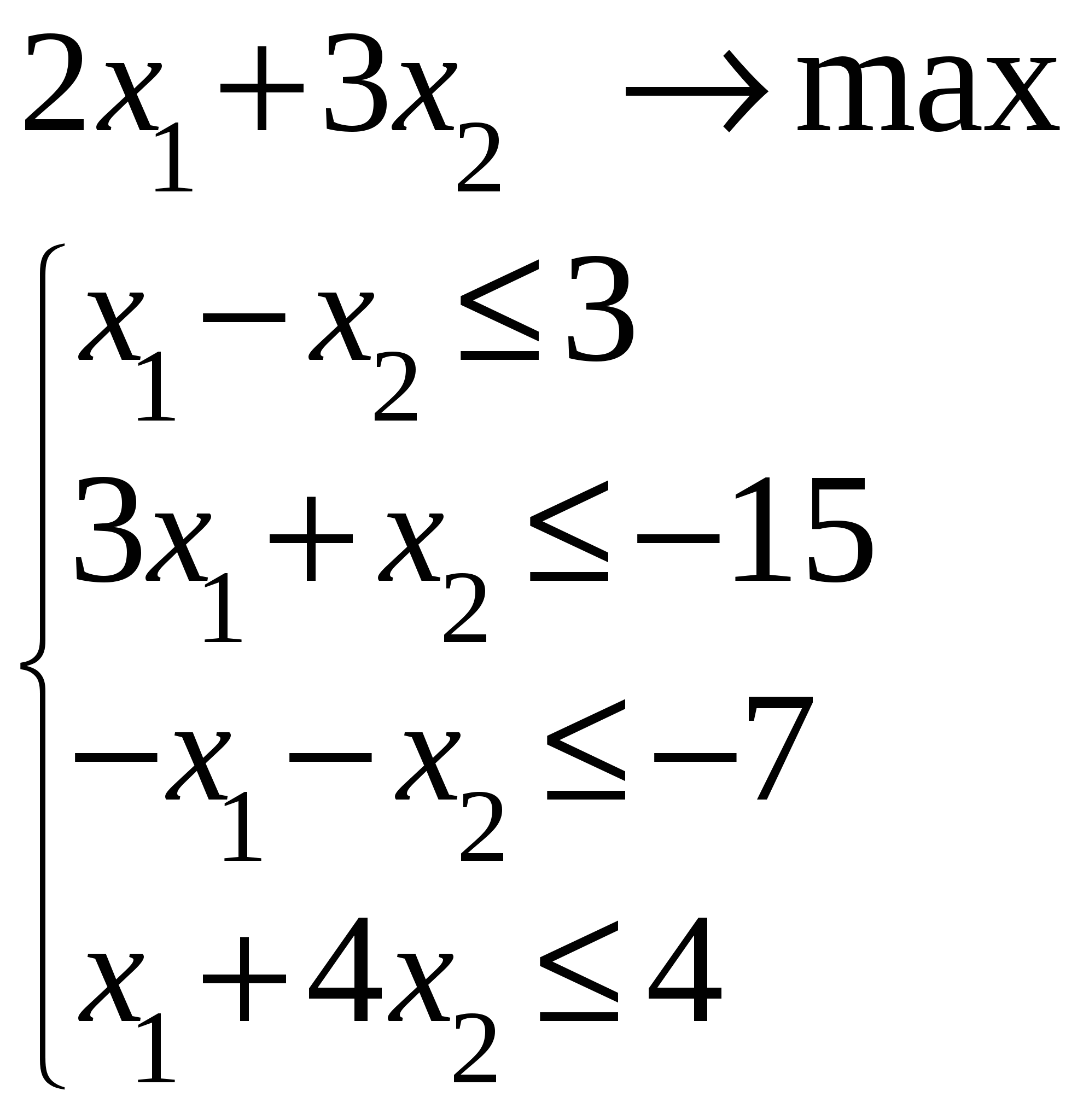



Что и требовалось доказать.

Прямая задача ЛП имеет вид:



Ограничения: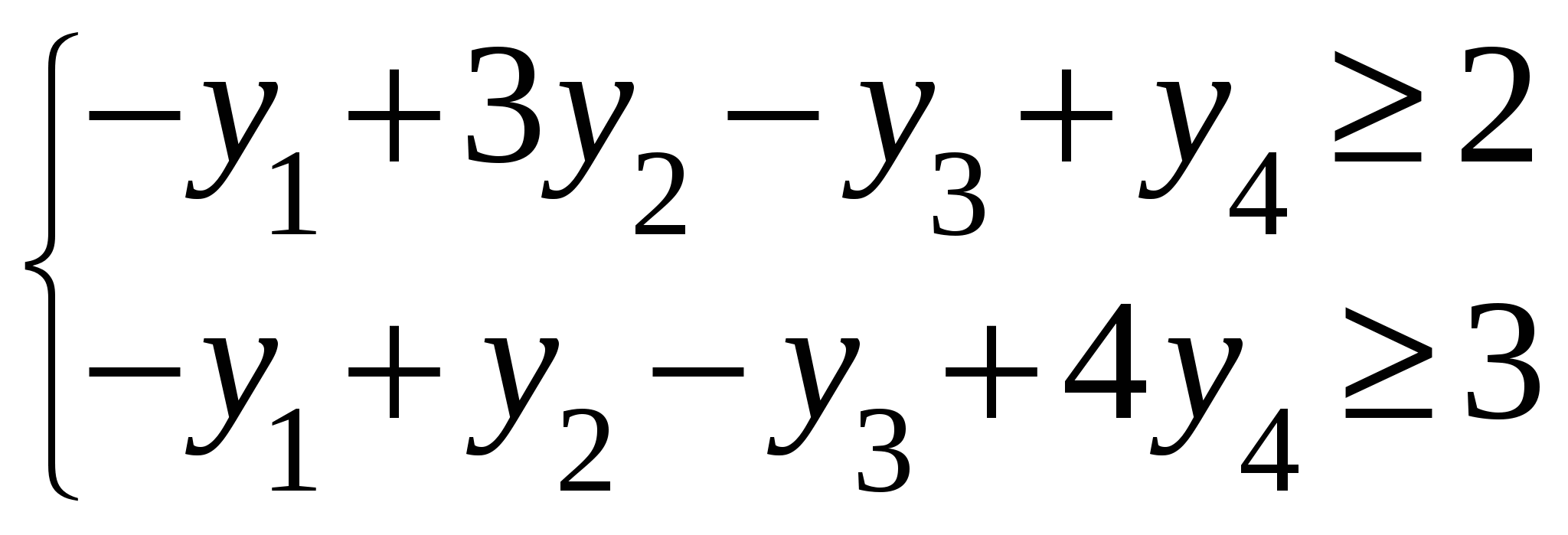





В результате получим следующие матрицы.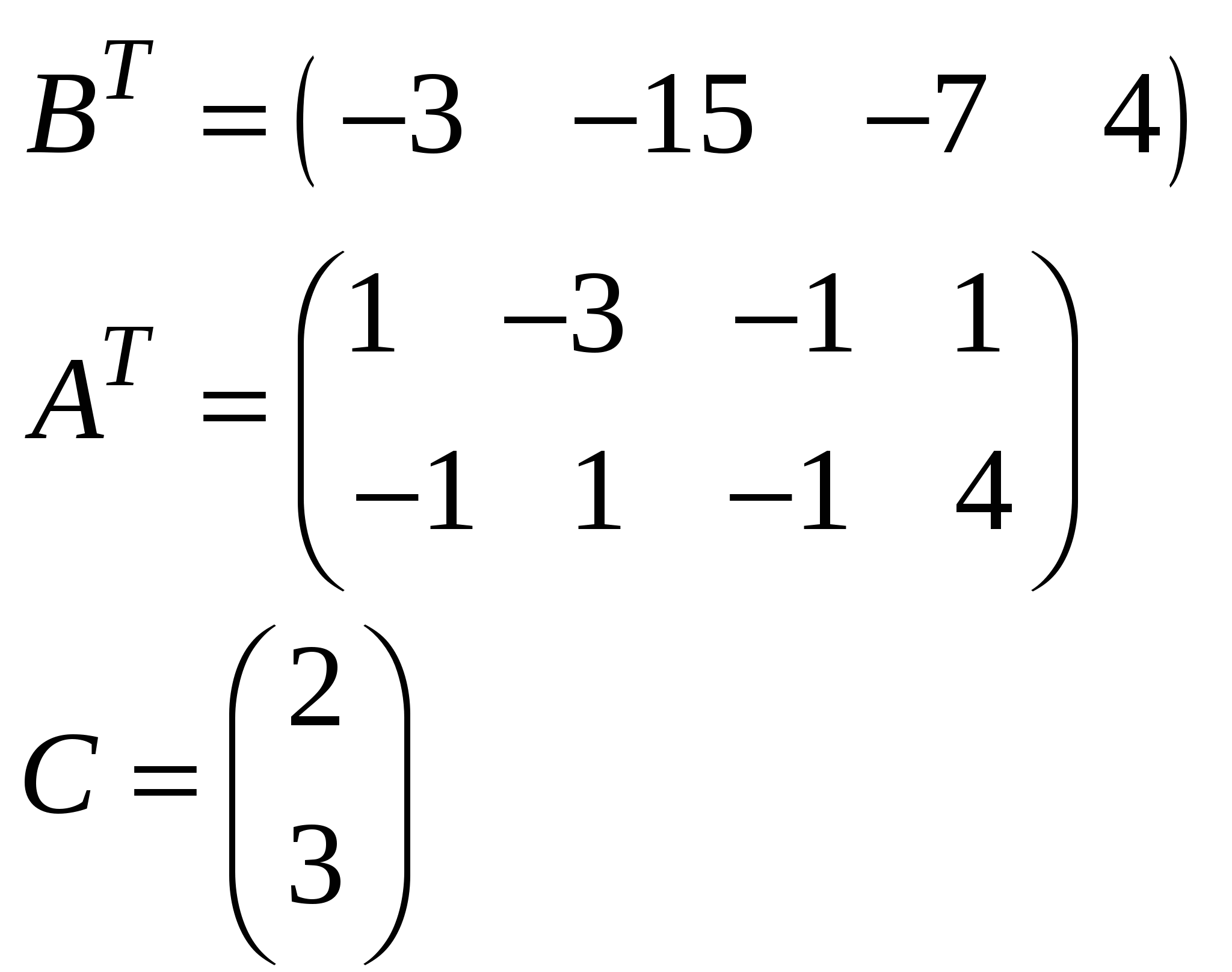



Для составления двойственной задачи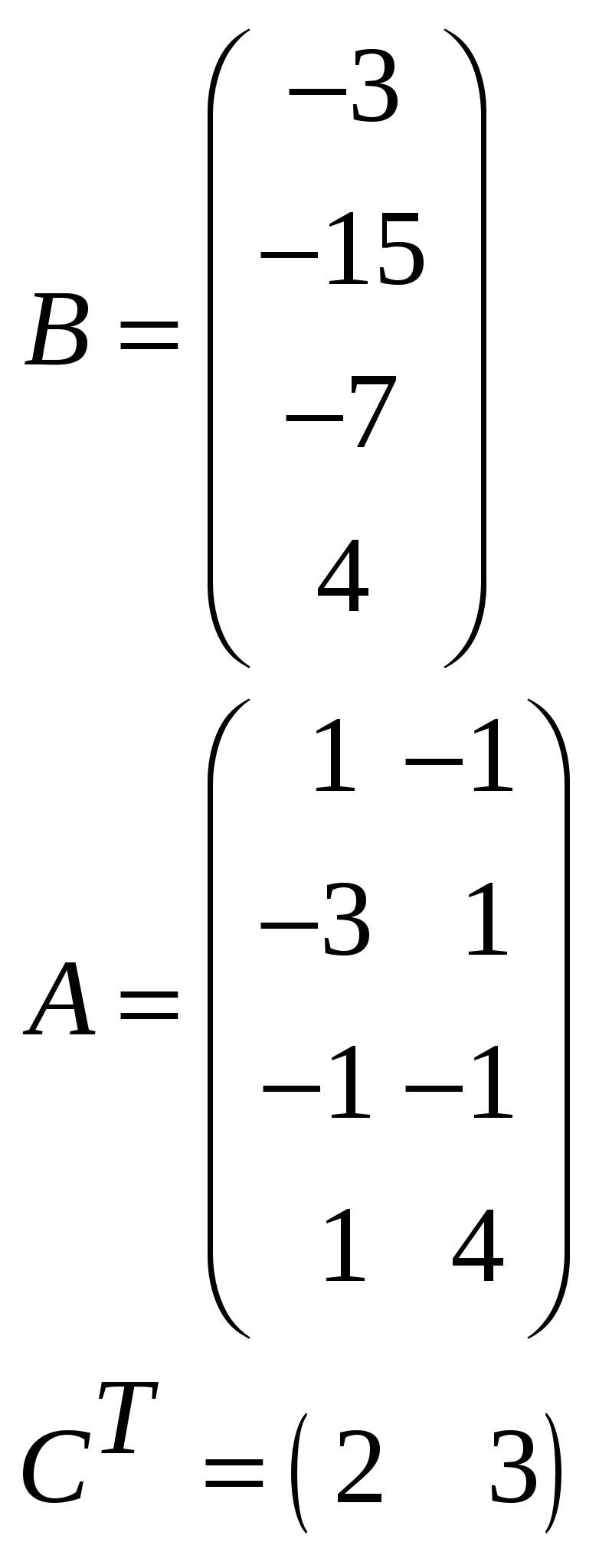



Следовательно, двойственная задача ЛП будет иметь вид: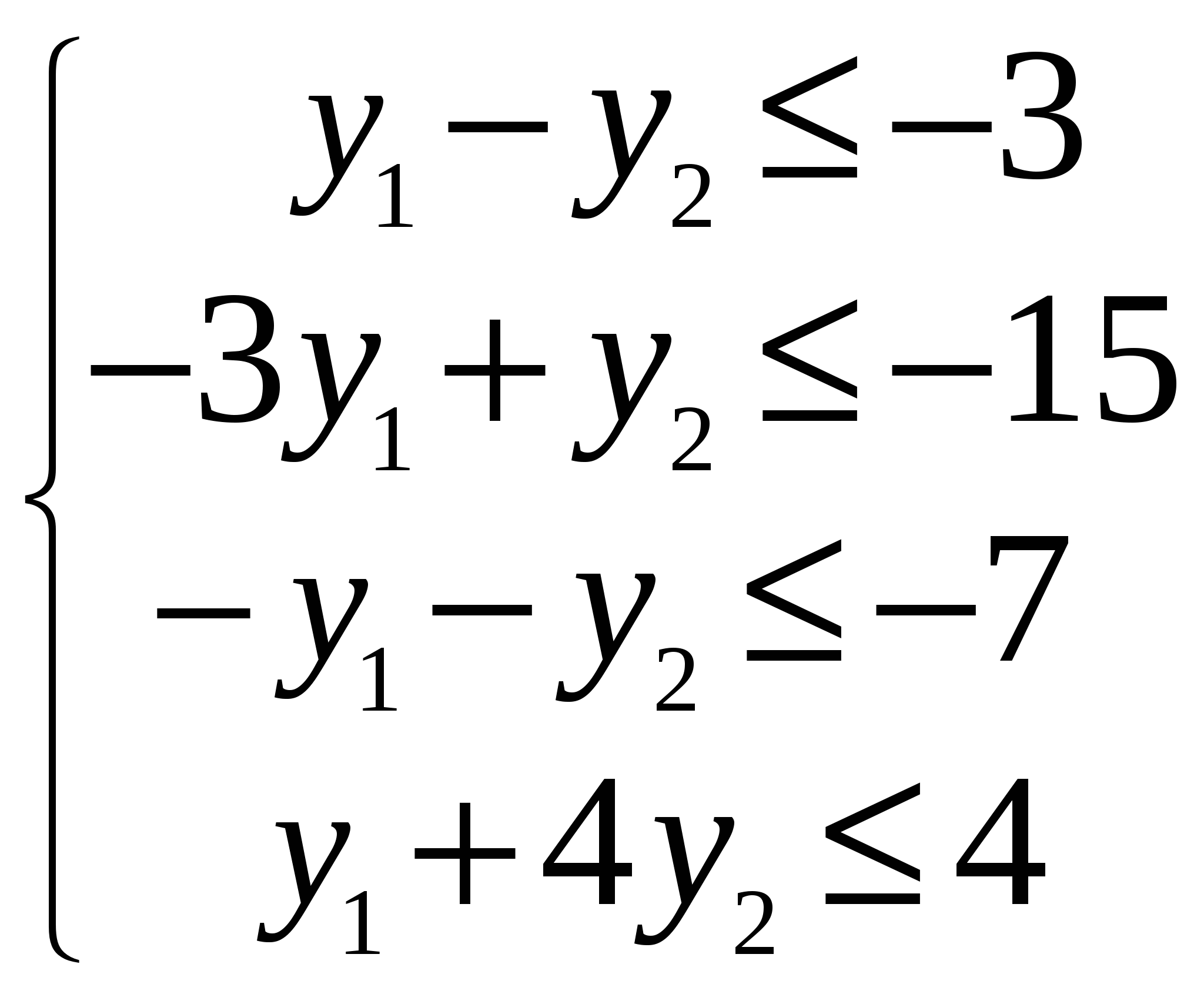







Прямая задача: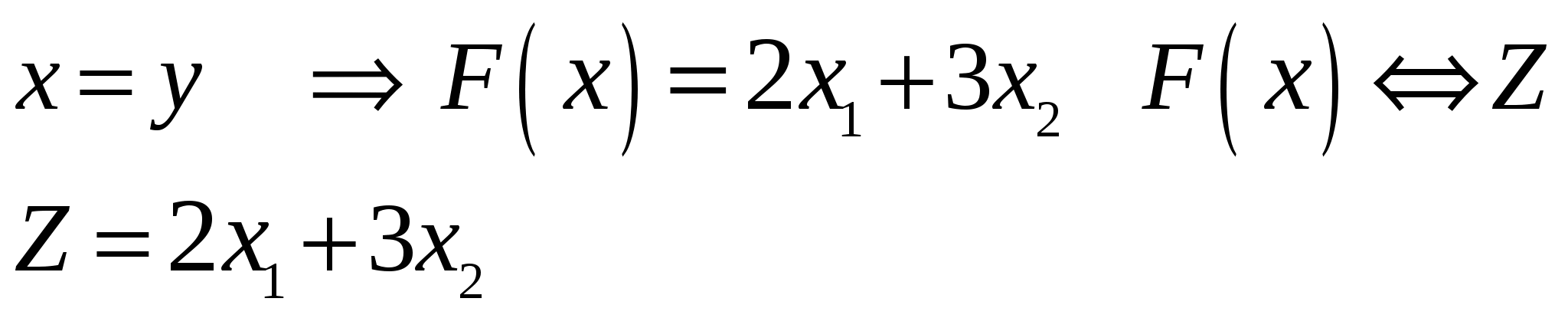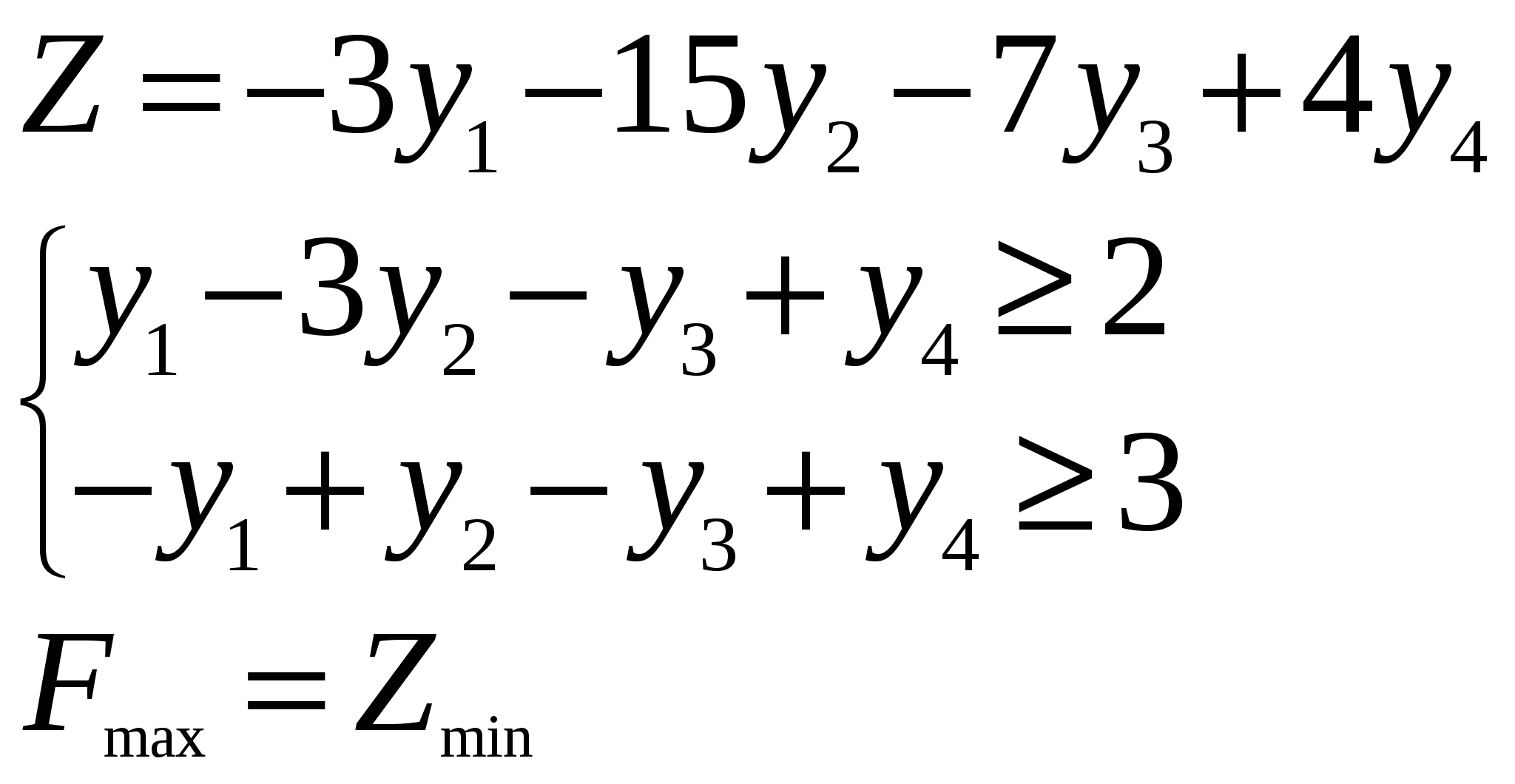






5.2.

Найти значения переменных 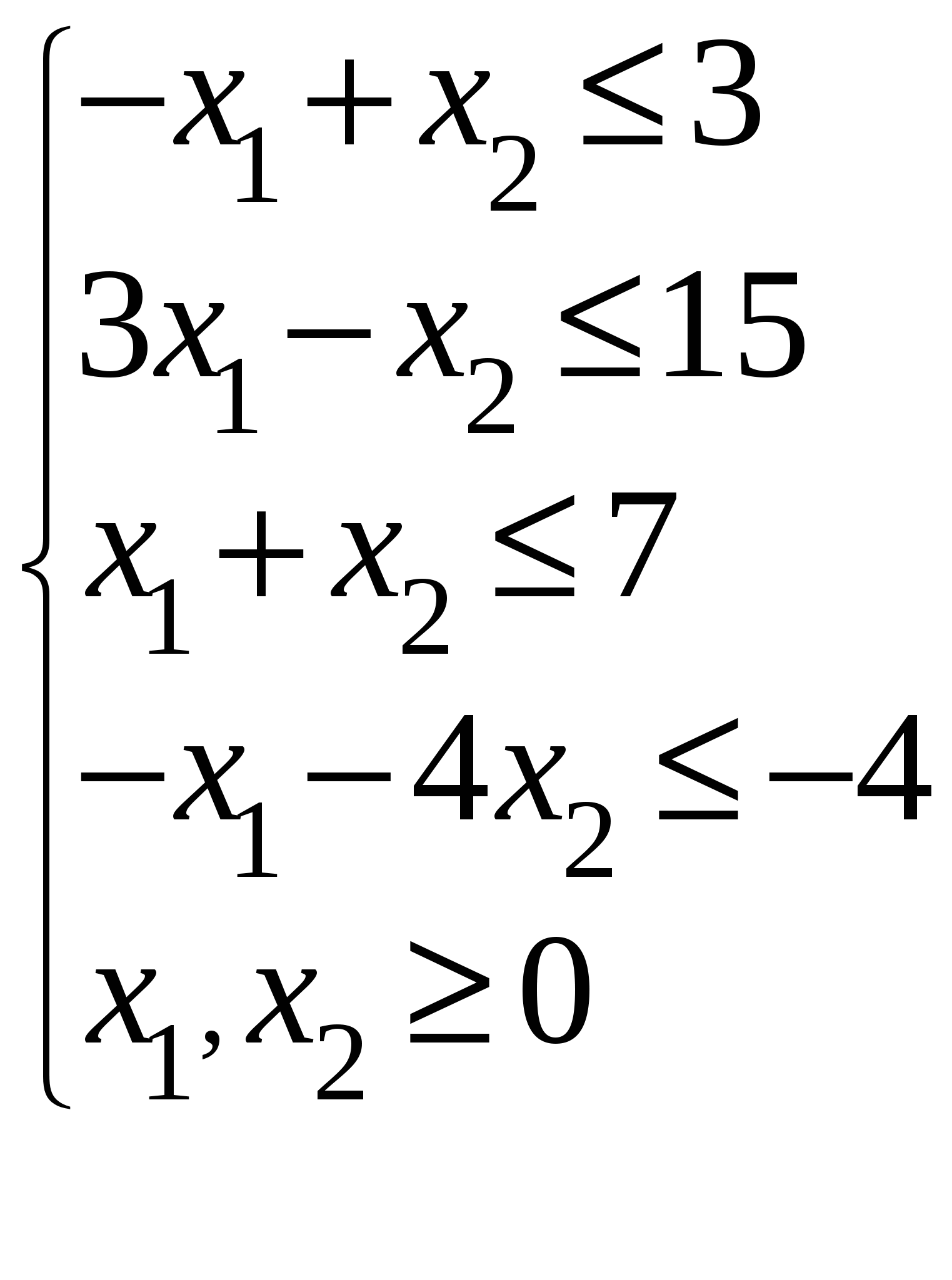, при которых функция





Шаг 1: избавляемся от отрицательных свободных членов, уменьшив на (-1).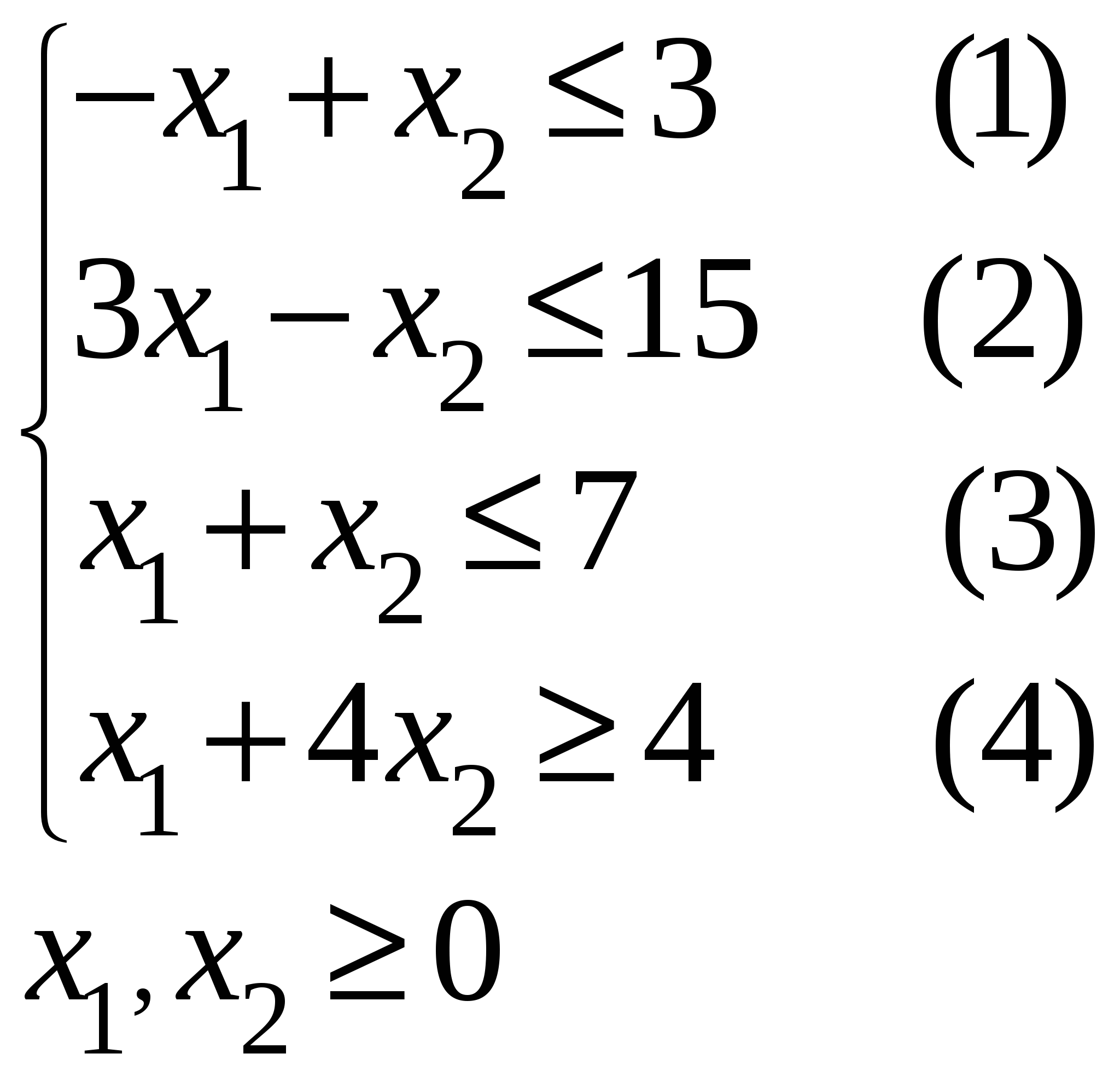



Шаг 2: Избавимся от неравенств в ограничениях, введя в ограничения 1,2,3,4 неотрицательные балансовые переменные ,