Линейная алгебра. Решение Строится многоугольная область допустимых значений на плоскости (рис. 1)

• Название: Решение Строится многоугольная область допустимых значений на плоскости (рис. 1)
• Дата: 03.04.2018
• Размер: 0.86 Mb.
• Имя файла: Линейная алгебра.doc
• Тип: Документы; #40227
• страница: 4 из 4

При проведении интерации 3:

БП							Решение
	0		0		0	0	-20

При проведении интерации 4:

БП							Решение
	0	0	0	0	-4	0	-28

Достигнуто оптимальное решение, т.к. в строке целевой функции нет положительных коэффициентов.

Ответ: 1.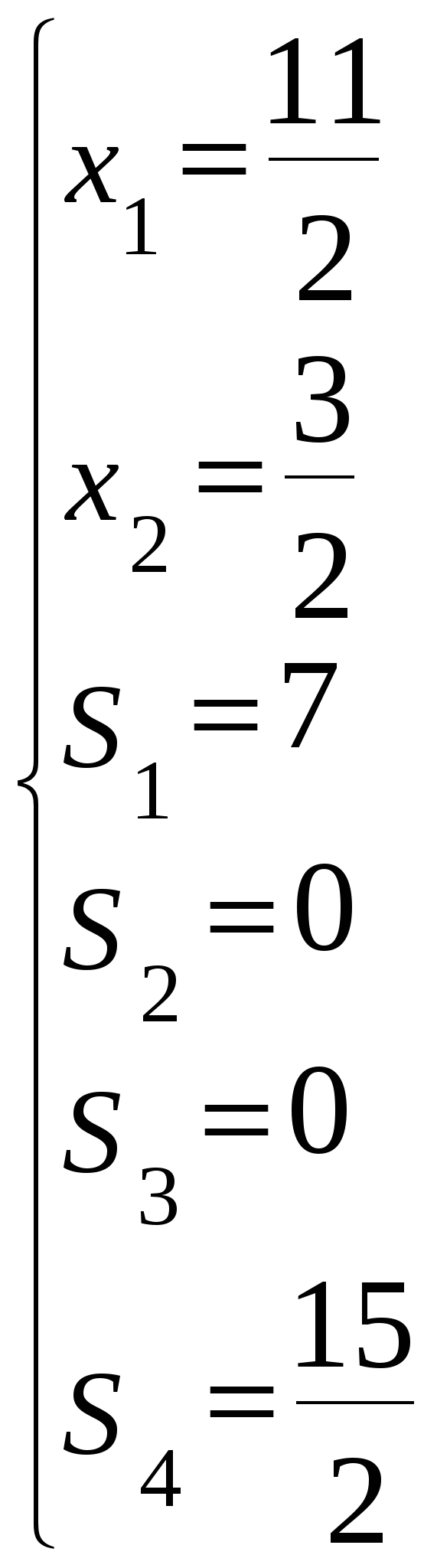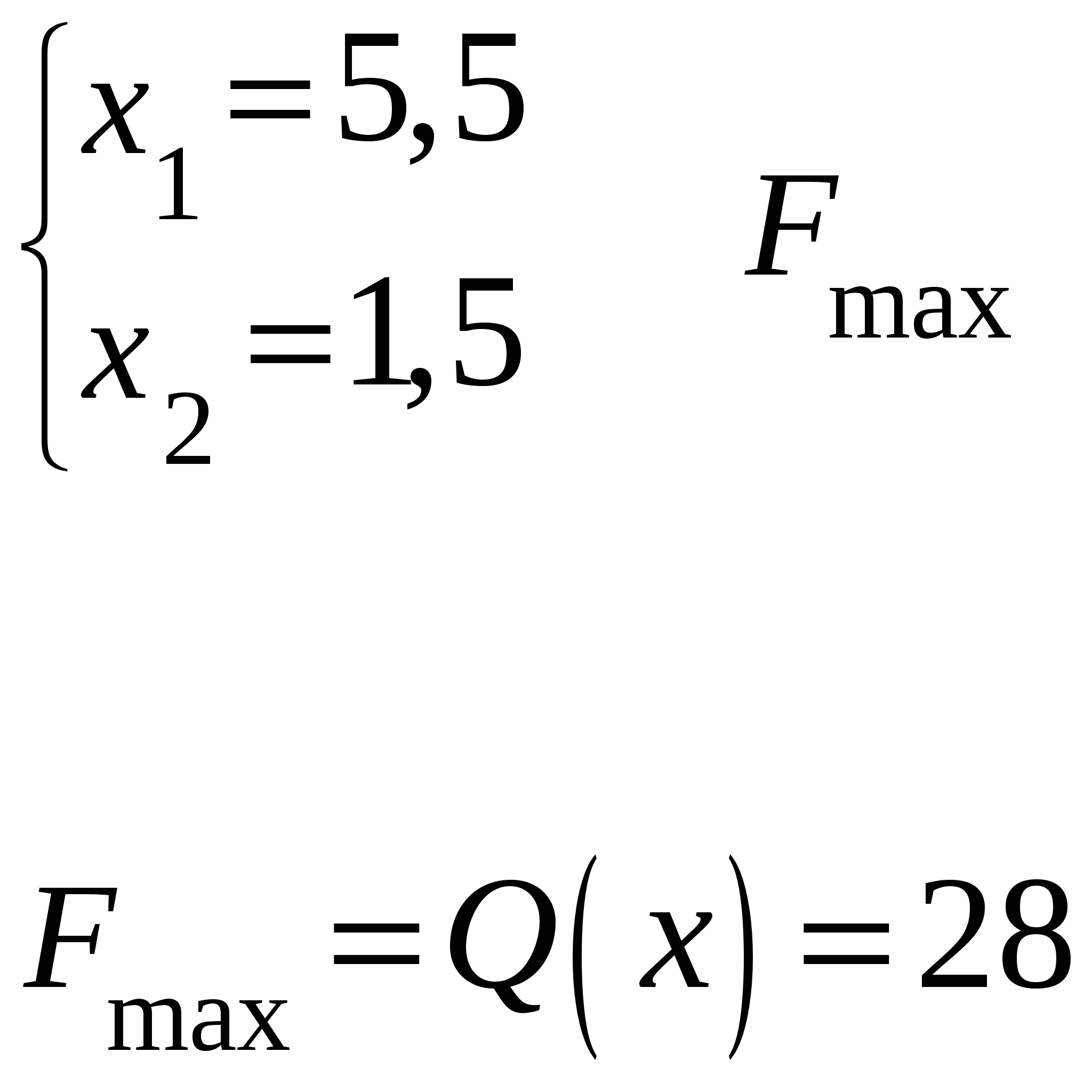



Ответ: 2. альтернативное решение получается после интерации 4 и 5.

Значение

БП							Решение
	0	0	0	0	-4	0	-28

Достигнуто оптимальное решение, т.к. в строке нет 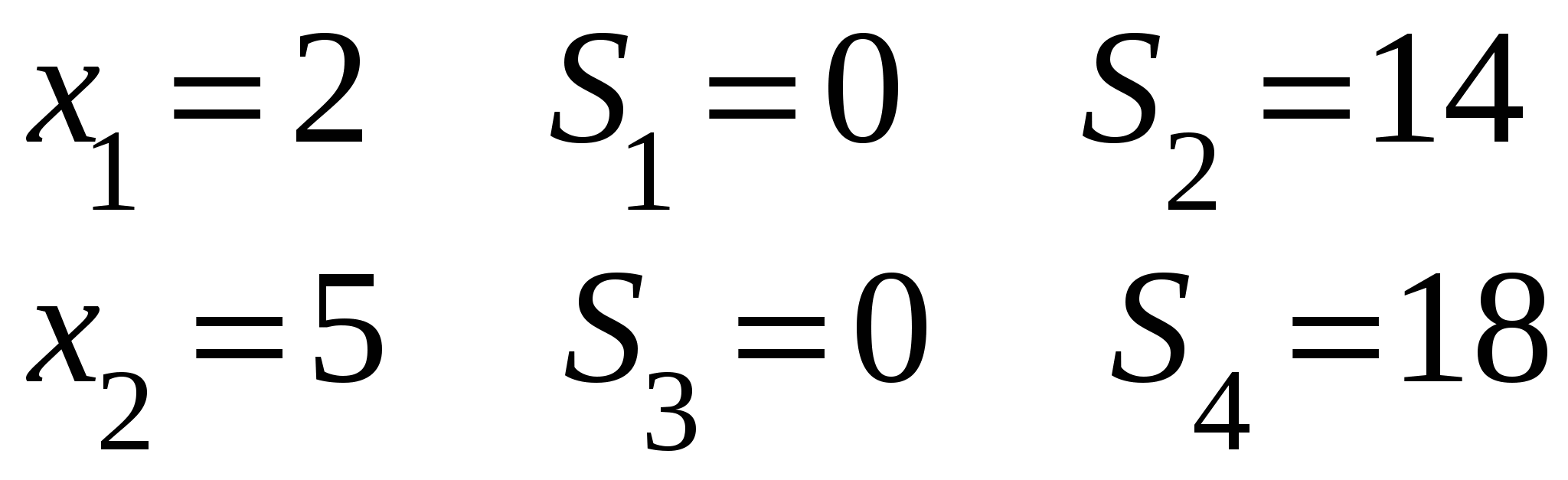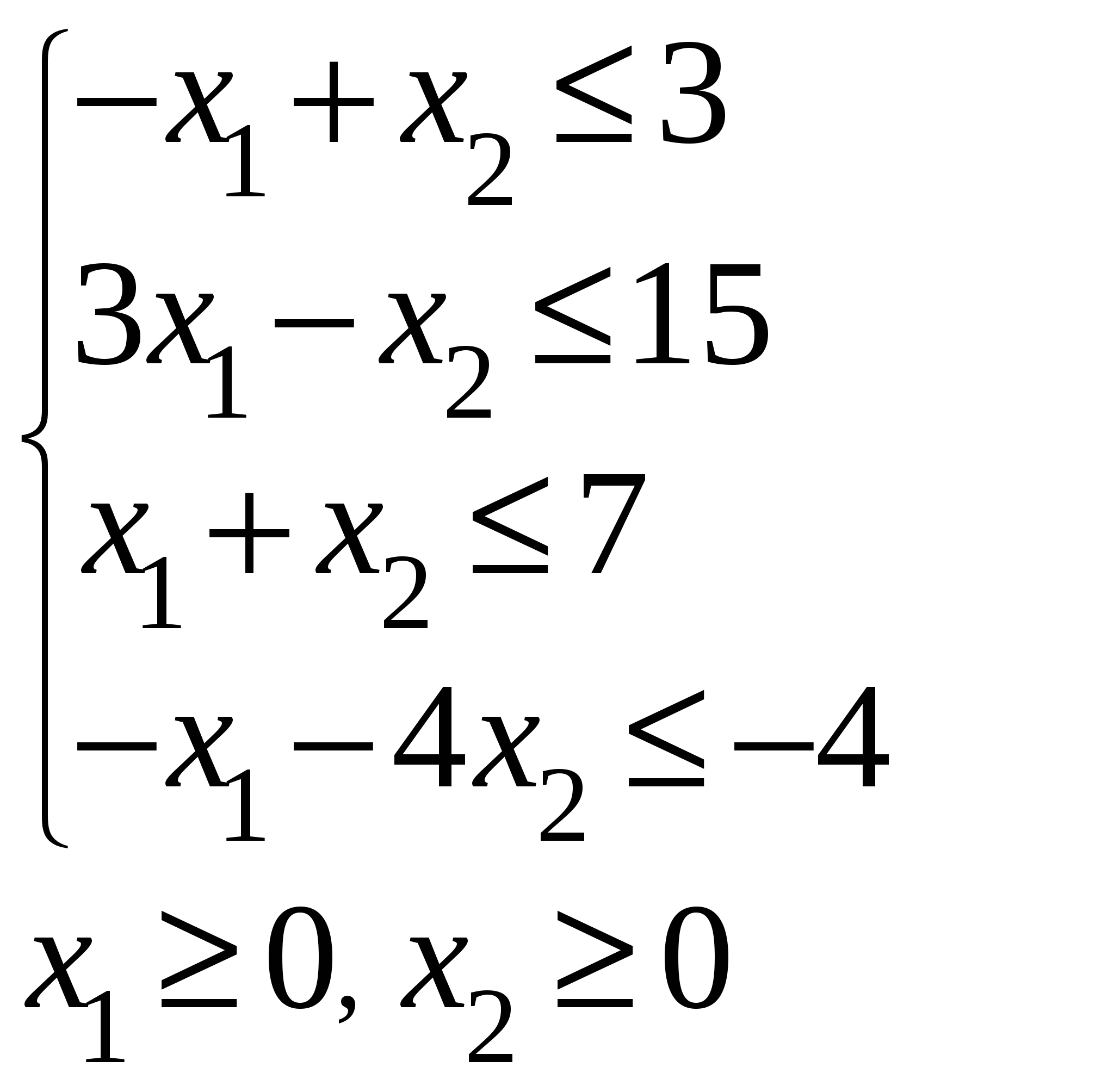положительных коэффициентов.



при







Приведем ограничения к виду ″″.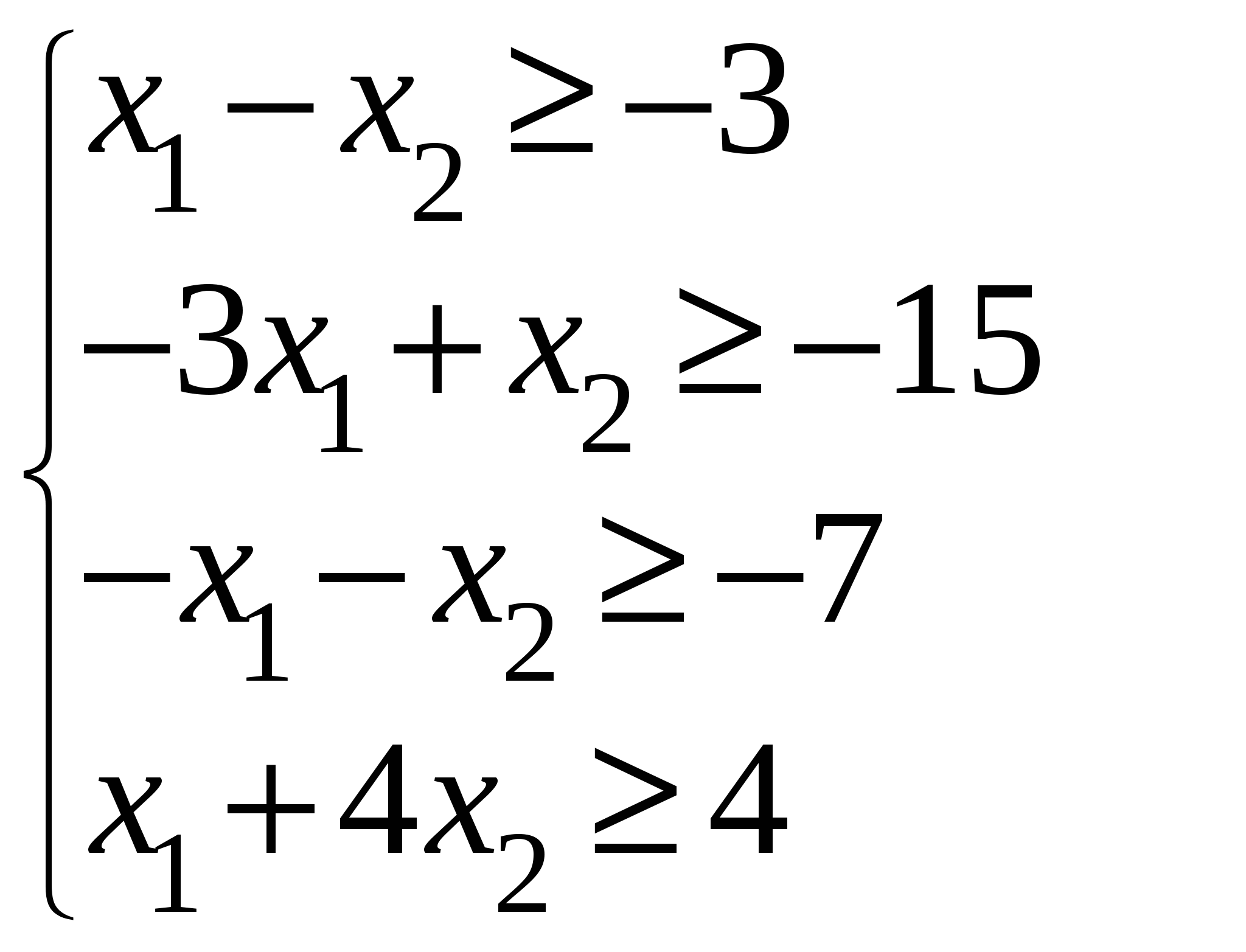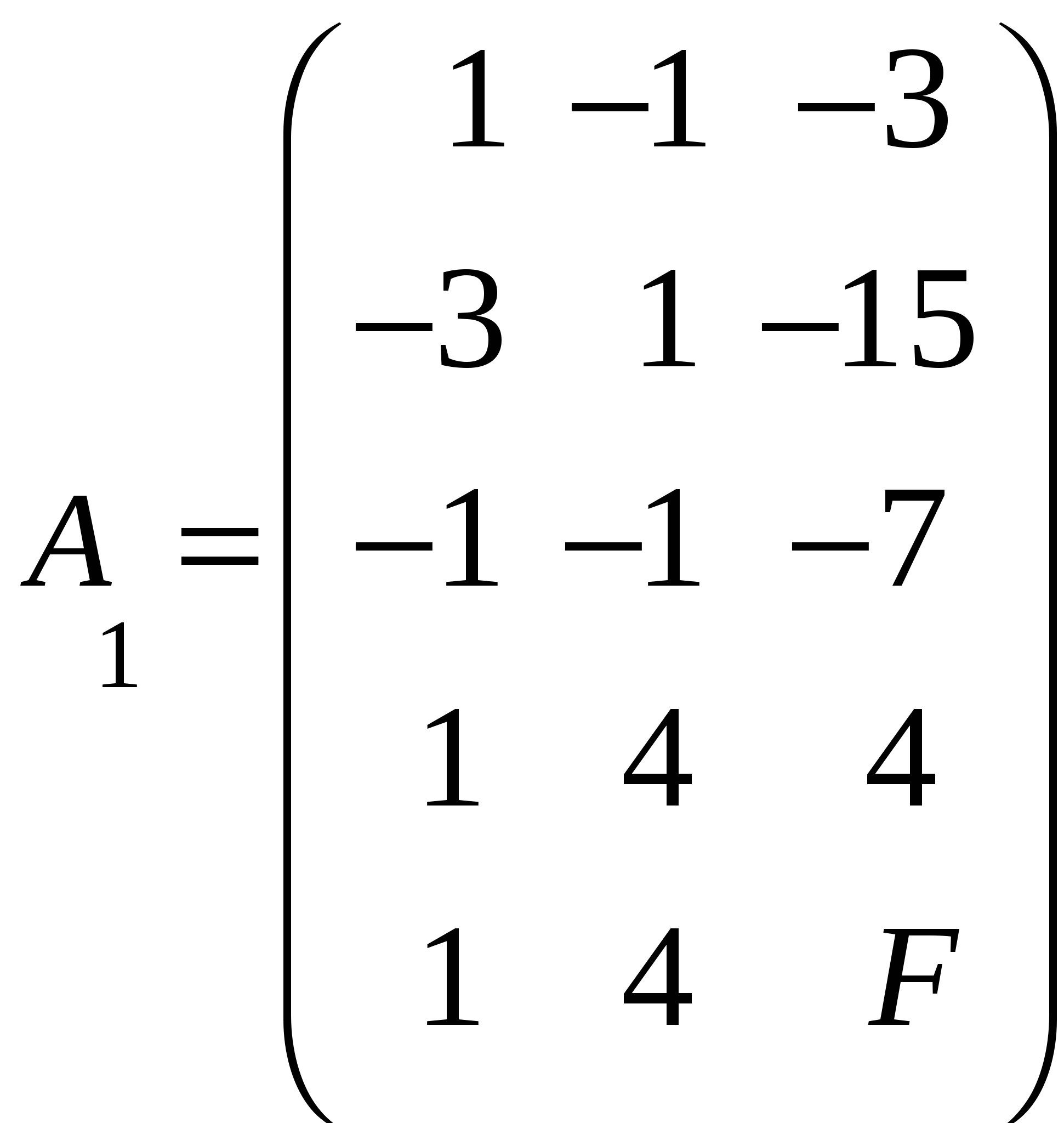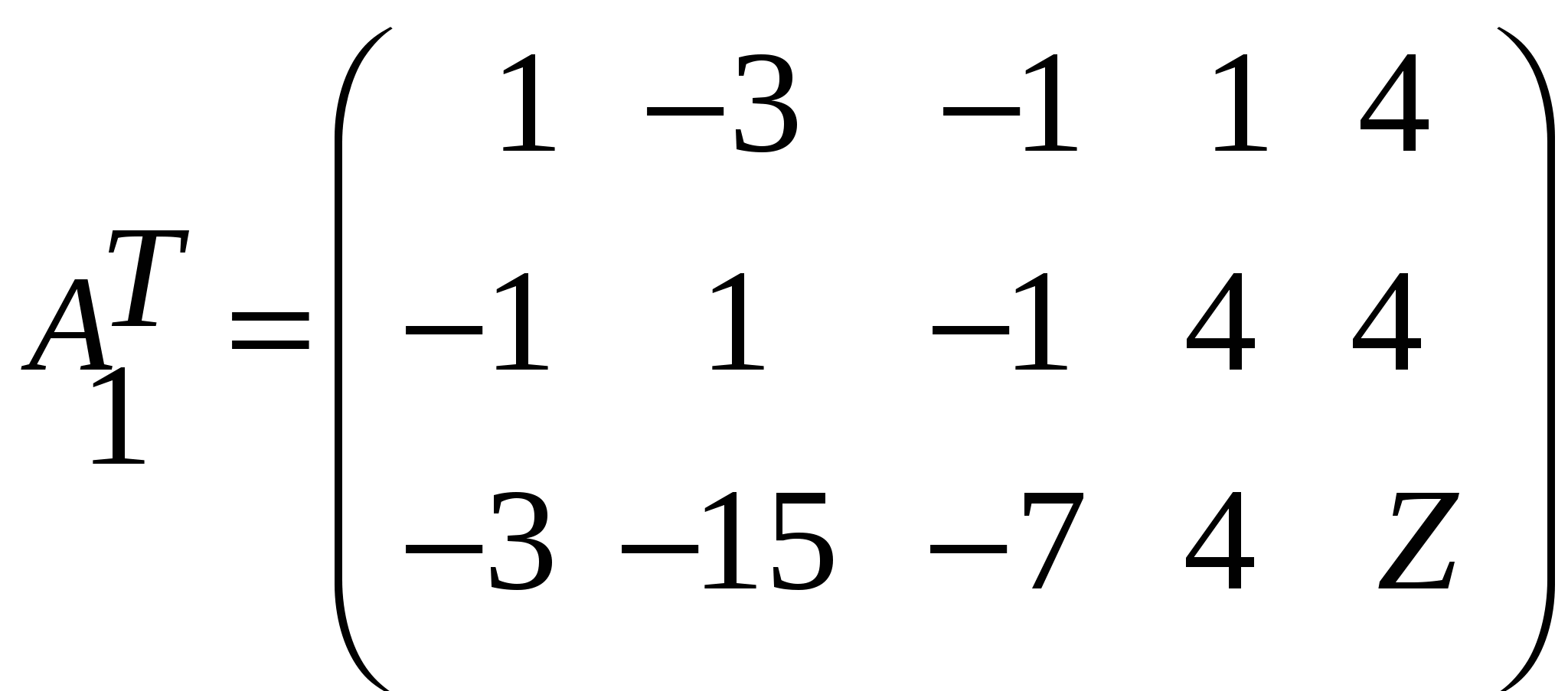







Двойственная задача: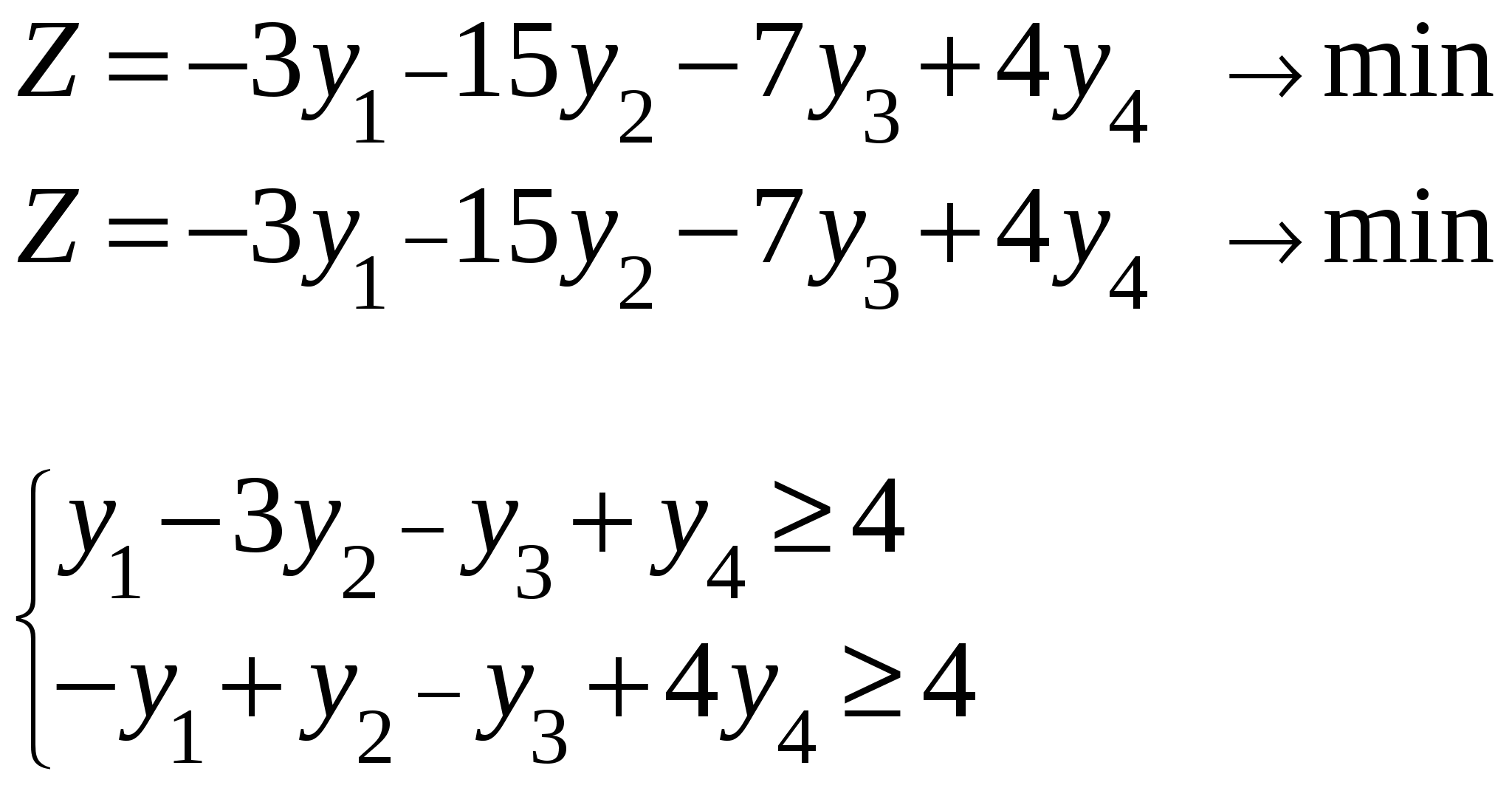



Введем дополнительные переменные .



Ограничения: (вводим дополнительные переменные).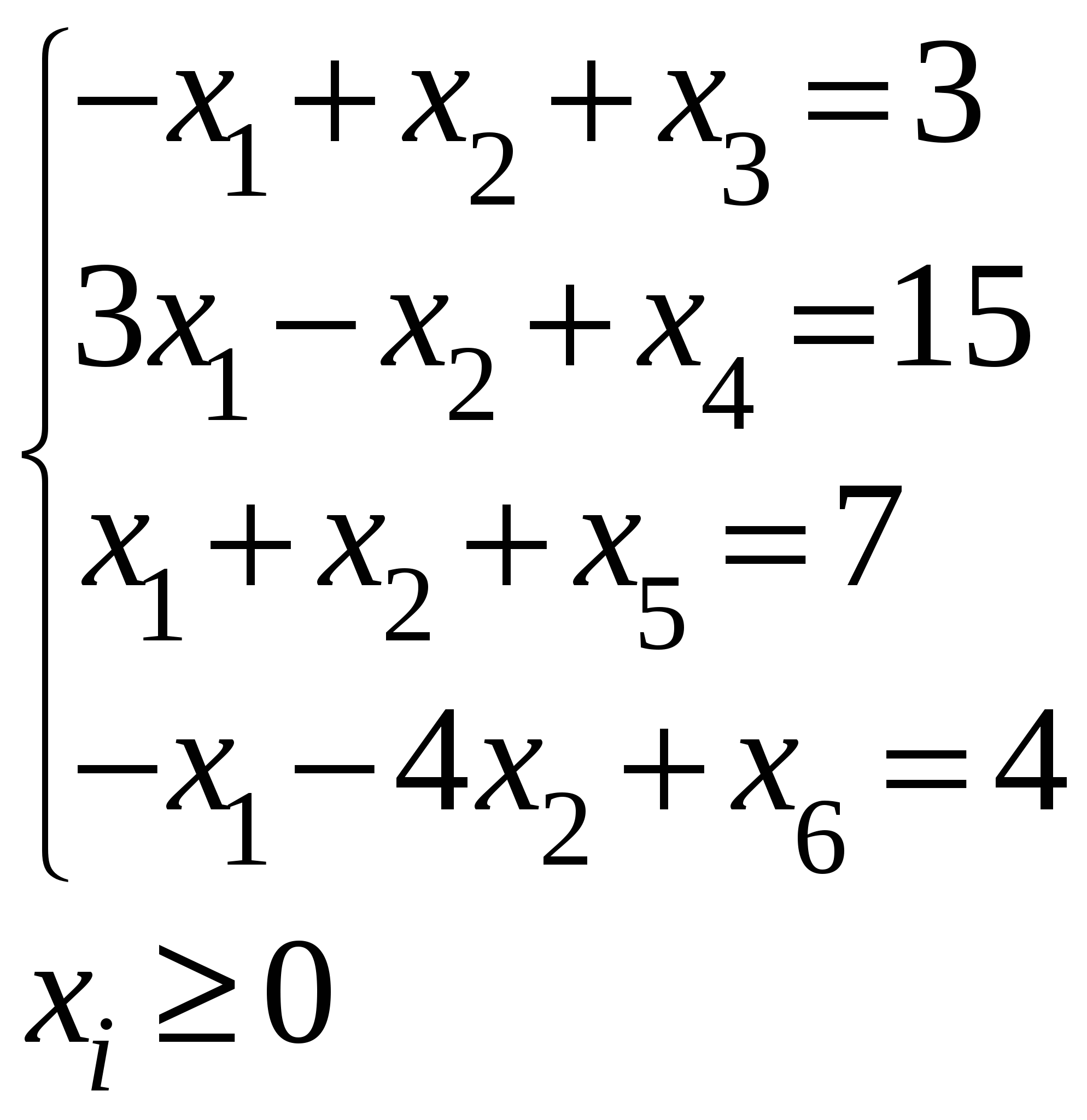



Составим симплекс-таблицу

Базисные переменные	Свободные члены
	3	-1	1
	15	3	-1
	7	1	1
	4	-1	-4
F	0	-4	-4

Т.к. в столбце свободных членов нет отрицательных элементов, то найдено допустимое значение. Т.к. в строке F есть отрицательные элементы, то полученное решение не оптимально.

Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в строке . А ведущая строка, отношение свободного члена к соответствующему элементу ведущего столбца.

Пересчитаем таблицу.

Базисные переменные	Свободные члены
	8
	5
	2
	9
F	20

Т.к. в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.

Т.к. в строке F есть отрицательные элементы, то полученное решение не оптимально.

Для определения ведущего столбца найдем ″″ по модулю отрицательный элемент в строке .

А ведущая строка, та у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.

Пересчитаем таблицу.

Базисные переменные	Свободные члены
	7
F	28	0	4

Найдем оптимальное решение:

F = 28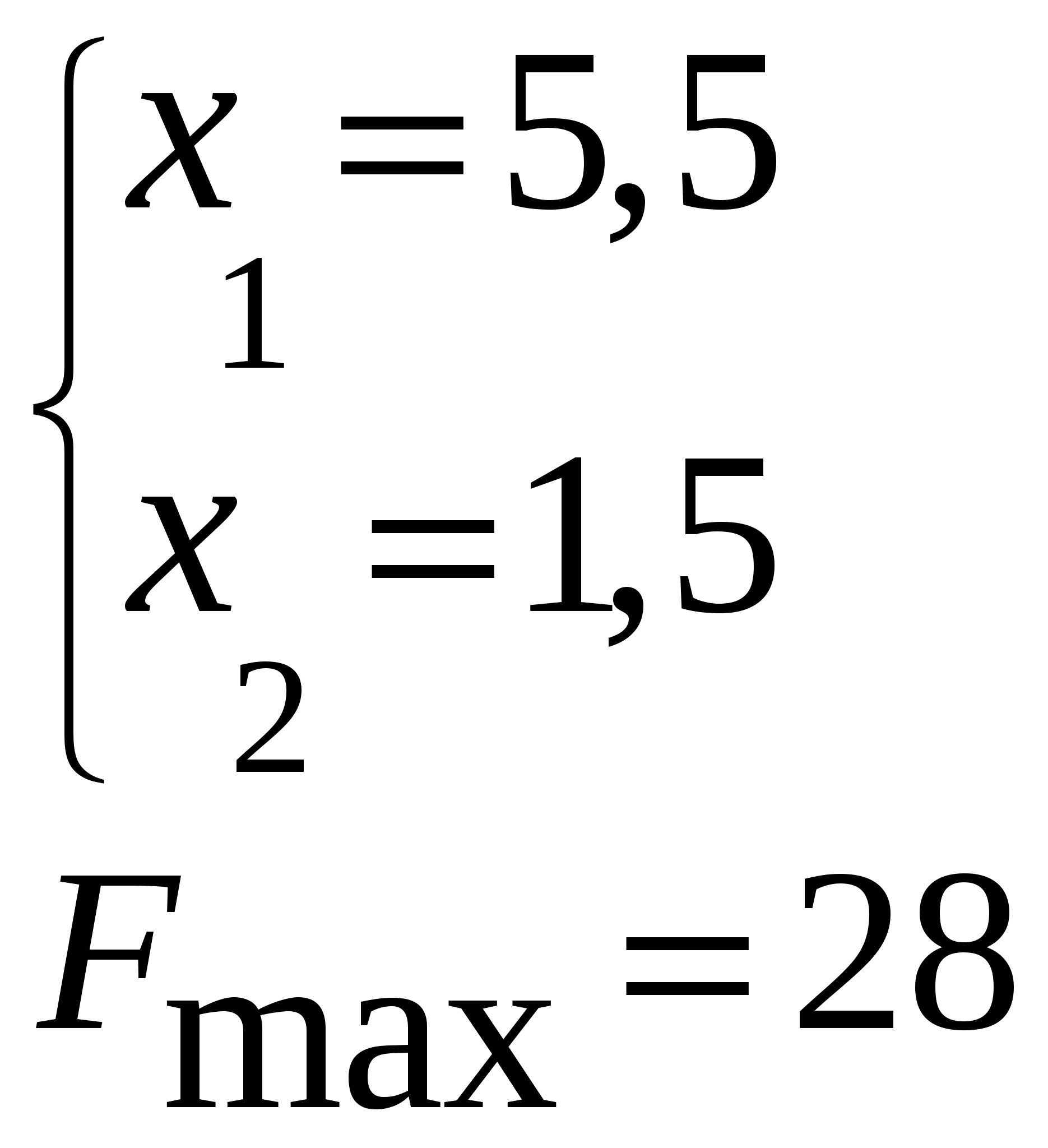





Мы решили задачу ЛП симплекс-методом двумя способами.

Пришли к выводу: что геометрическое решение ЗЛП и аналитическое решение (симплекс-методом) совпадают.

Если в одной из двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырождено.