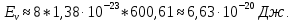|
|
Задание 1 Материаловедение Росдистант. Задание 1 Материаловедение и ТКМ 1. Решение Индексы Миллера, заданные по условию равны Откуда
Тема 1. Кристаллическое строение твёрдых тел
Задание
Часть 1. Нарисовать плоскость с заданными индексами, проходящую через узел с заданными координатами.
Вариант 1: Плоскость (102), проходящую через узел [[001]].
Решение
Индексы Миллера, заданные по условию равны:
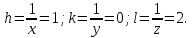
Откуда
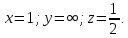
Вследствие периодичности кристаллической решетки каждая плоскость имеет очень много параллельных ей плоскостей − семейство плоскостей. Индексы кристаллографической плоскости (hkl) характеризуют как плоскость, ближайшую к началу координат, так и все данное семейство плоскостей.
Ближайшая плоскость из семейства (102) отсекает на оси OX отрезок 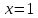 ; на оси OZ отрезок ; на оси OZ отрезок 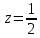 ; с осью OY плоскость не пересекается. ; с осью OY плоскость не пересекается.
Через узел [[001]] будет проходить следующая из семейства плоскостей (102) с отсекаемыми отрезками:
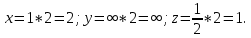
Нарисуем эту плоскость:
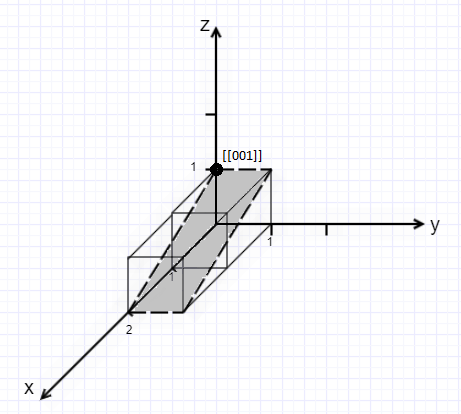
Рисунок 1
Часть 2. Зарисовать кристаллические модификации элементов, обозначить параметры решеток. Указать температуру полиморфного превращения и температуру плавления. Рассчитать изменение объема при полиморфном превращении.
Вариант 1: Натрий.
Решение
Кристаллическая решетка (КР) №1.
Объемноцентрированная кубическая кристаллическая решетка (ОЦК).
Основу ОЦК-решетки составляет элементарная кубическая ячейка, в которой атомы находятся в вершинах куба и еще один атом в центре его объема (рисунок 2).
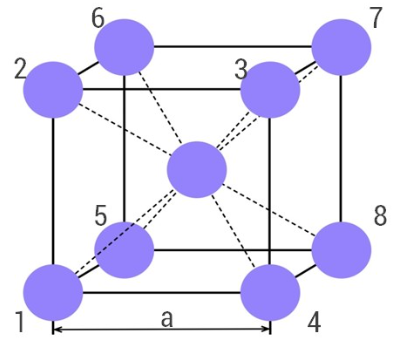
Рисунок 2
Параметры КР:
Период КР: 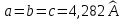 ; ;
Углы между главными осями КР: 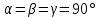 ; ;
Базис: 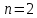 ; ;
Координационное число: 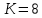 ; ;
Коэффициент компактности: 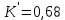 . .
Кристаллическая решетка (КР) №2.
Гексагональная КР (рисунок 3).
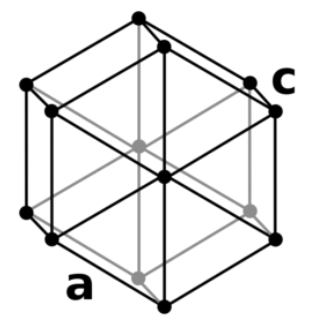
Рисунок 3
Параметры КР:
Период КР: 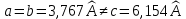 ; ;
Углы между главными осями КР: 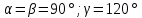
Базис: 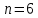 ; ;
Координационное число: 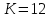 ; ;
Коэффициент компактности: 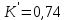 . .
Температура плавления: __97,81 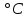 __. __.
Температура полиморфного превращения: __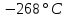 __. __.
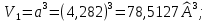
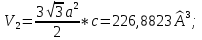
Относительное изменение объема при полиморфном превращении:
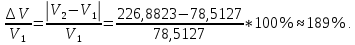
Объем увеличился на 189%.
Тема 2. Дефекты кристаллического строения
Задание
Часть 1. Рассчитайте равновесную долю вакансий при температурах: –196 °C; +20 °C; 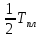 ; ; 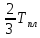 ; 0,9 ; 0,9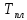 ; ; 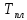 (по абсолютной шкале). Постройте график зависимости доли вакансий от температуры. Расчёт сделайте для: (по абсолютной шкале). Постройте график зависимости доли вакансий от температуры. Расчёт сделайте для:
Вариант 1: алюминия.
Решение
Равновесная концентрация вакансий определяется экспоненциальной формулой:
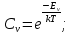
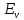 – энергия образования вакансии – энергия образования вакансии
(для алюминия 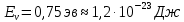 ); );
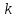 – постоянная Больцмана ( – постоянная Больцмана (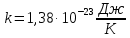 ). ).
Следовательно, при температуре:
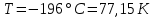 : :
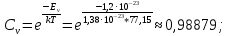
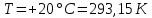 : :
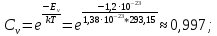
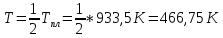 : :
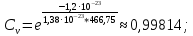
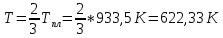 : :
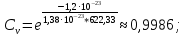
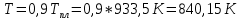 : :
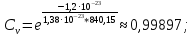
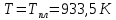 : :
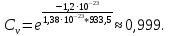
График зависимости доли вакансий от температуры:
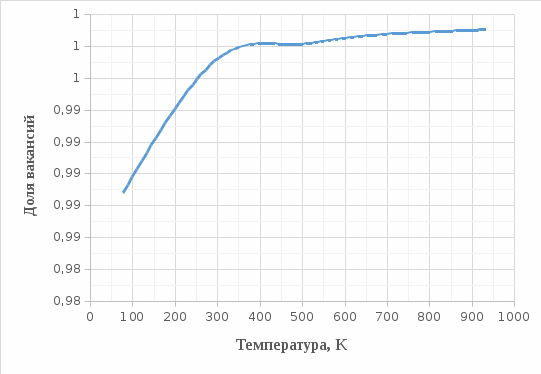
Рисунок 4
Часть 2. В расчёте на 1 см3 металла оцените: а) энергию дислокаций при их максимально возможной плотности 1012 см; б) энергию вакансий при их максимально возможной равновесной концентрации (вблизи температуры плавления). Расчёт сделайте для:
Вариант 1: свинца.
Решение
а) Энергия дислокации определяется выражением:
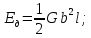
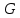 – модуль сдвига (для свинца – модуль сдвига (для свинца 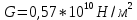 ); );
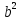 – квадрат модуля вектора Бюргерса дислокации; так как свинец имеет гранецетрированную кубическую кристаллическую решетку, то – квадрат модуля вектора Бюргерса дислокации; так как свинец имеет гранецетрированную кубическую кристаллическую решетку, то
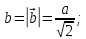
для свинца период КР: 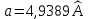 . Тогда . Тогда
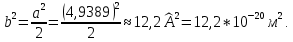
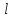 – длина дислокации; эту величину найдем из формулы плотности дислокации: – длина дислокации; эту величину найдем из формулы плотности дислокации:
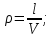
тогда 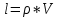 ; ;
по условию 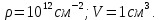 Следовательно, Следовательно,
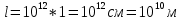
Теперь можем вычислить энергию дислокации свинца:
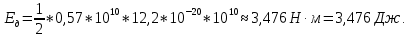
б) Экспериментально установлено, что для ГЦК металлов выполняется следующее соотношение:
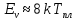
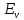 – энергия образования вакансии; – энергия образования вакансии;
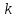 – постоянная Больцмана ( – постоянная Больцмана (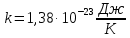 ); );
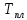 – температура плавления свинца ( – температура плавления свинца (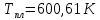 ). ).
Тогда энергия образования вакансии:
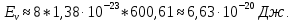
|
|
|
 Скачать 151.58 Kb.
Скачать 151.58 Kb.
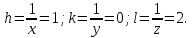
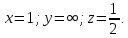
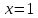 ; на оси OZ отрезок
; на оси OZ отрезок 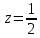 ; с осью OY плоскость не пересекается.
; с осью OY плоскость не пересекается. 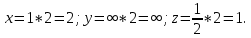


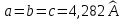 ;
;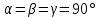 ;
;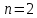 ;
;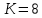 ;
;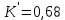 .
.
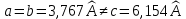 ;
;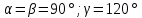
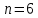 ;
;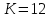 ;
;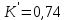 .
.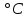 __.
__. 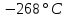 __.
__.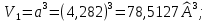
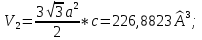
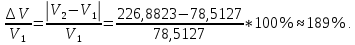
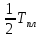 ;
; 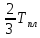 ; 0,9
; 0,9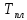 ;
; 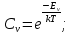
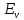 – энергия образования вакансии
– энергия образования вакансии 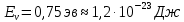 );
);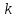 – постоянная Больцмана (
– постоянная Больцмана (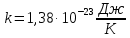 ).
).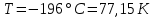 :
: 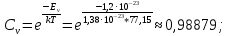
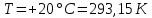 :
: 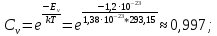
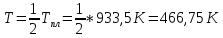 :
: 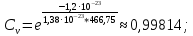
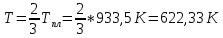 :
: 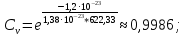
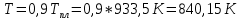 :
: 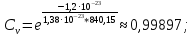
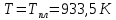 :
: 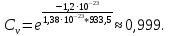

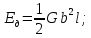
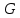 – модуль сдвига (для свинца
– модуль сдвига (для свинца 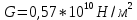 );
);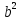 – квадрат модуля вектора Бюргерса дислокации; так как свинец имеет гранецетрированную
– квадрат модуля вектора Бюргерса дислокации; так как свинец имеет гранецетрированную 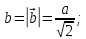
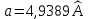 . Тогда
. Тогда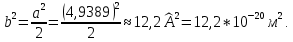
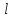 – длина дислокации; эту величину найдем из формулы плотности дислокации:
– длина дислокации; эту величину найдем из формулы плотности дислокации: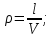
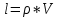 ;
;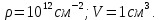 Следовательно,
Следовательно,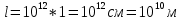
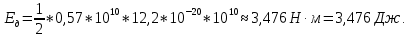
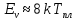
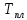 – температура плавления свинца (
– температура плавления свинца (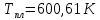 ).
).