ИДЗ ОЭиРМ 2023 пункты 1-2. Санктпетербургский государственный электротехнический университет лэти им. В. И. Ульянова
 Скачать 129.94 Kb. Скачать 129.94 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра МИТ ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ по дисциплине «Основы электроники и радиоматериалы» Тема: Исследование контактных явлений в структуре металл-проводник Вариант 22, шифр 13, 1, 1Студент гр. 1111 Фёдоров В.А. Преподаватель Рассадина А.А. Санкт-Петербург 2023 Исходные данныеВариант 22, шифр (13, 1, 1) Таблица 1. Некоторые свойства металла
Таблица 2. Свойства собственного полупроводника
Таблица 3. Концентрация n- и p-примесей в полупроводниках
Определение класса симметрии заданных материалов, построение прямой и обратной элементарной ячейки заданных материалов. Определение размера Зоны Бриллюэна в направлениях X, L, К. Металл - Вольфрам Таблица 1.1.
Параметр решетки: 𝑎=3,16∗10−10м Формула симметрии: 3L4 4L3 9P Кристалл вольфрама имеет объёмоцентрированную кубическую решетку. Она отвечает ОЦК-решётке Бравэ с одноатомным базисом. Кратчайшее межатомное расстояние — вдоль диагоналей граней куба (110). Координационное число для ОЦК-решётки z =8: каждый атом имеет 4 ближайших соседей в своём слое и по 2 — в выше- и нижележащих слоях. Решетки ГЦК и ОЦК дуальны, следовательно, обратное пространство для ГЦК будет объемноцентрированное кубическое (ОЦК). В объёмноцентрированной кубической (ГЦК) структуре атомы расположены в вершинах и в центре элементарной ячейки, поэтому кратчайшее расстояние между ними — вдоль диагоналей куба(111) . Координационное число равно 12. В элементарной ячейке 2 атома. Базисные векторы для решетки ОЦК: 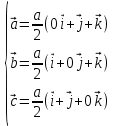 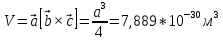 Базисные векторы для обратной решетки: 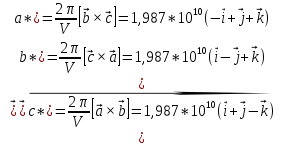 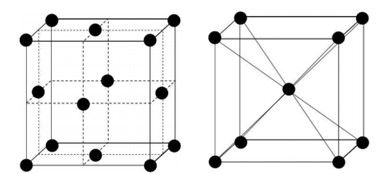 Рис. 1. Обратная решетка вольфрама ГЦК Рис. 2. Прямая решетка вольфрама ОЦК Определение размера Зоны Бриллюэна в направлениях X, L, К. 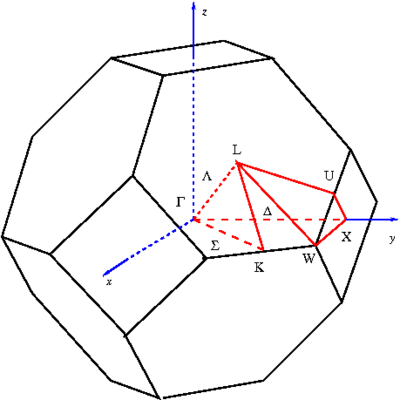 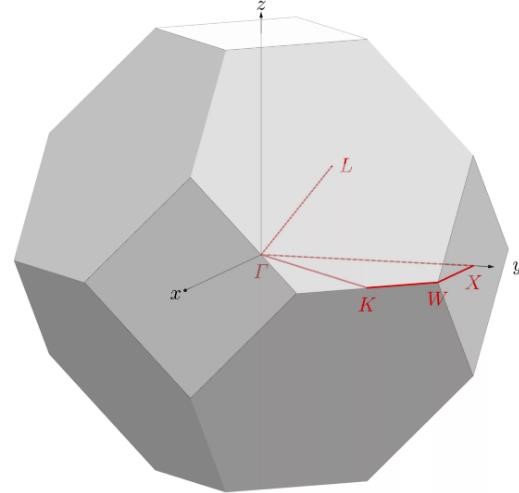 Рис. 4. Зона Бриллюэна для вольфрама Направление X (0; 1; 0): 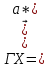 Направление L (1; 1; 1): Направление L (1; 1; 1): 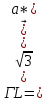 Направление K (1;1;0): 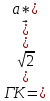 2. Полупроводник – Кремний Таблица 1.2.
Формула симметрии: 3L4 4L3 9P Постоянная решетки: 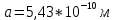 Базисные векторы для решетки ГЦК: 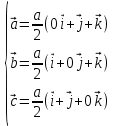 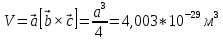 Базисные векторы для обратной решетки ОЦК: 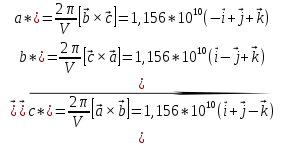  Рис. 5. Прямая и обратная решетки кремния Определение размера Зоны Бриллюэна в направлениях X, L, К.   Рисунок 6. Зона Бриллюэна для кремния Направление X (0; 1; 0): 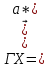 Направление L (1; 1; 1): 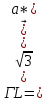 Направление K (1;1;0): 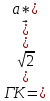 2. Определение концентрации электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов. Поверхность Ферми не является реальной поверхностью, а лишь наглядной иллюстрацией поведения электронов в металлах Найдём концентрацию электронов из условия касания зоны Бриллюэна и сферы Ферми для вольфрама. Радиус сферы Ферми связан с концентрацией электронов: Для ГЦК выбираем наименьшее значение волнового вектора в направлениях к характерным точкам. Сфера Ферми должна касаться первой зоны Бриллюэна, отсюда мы можем приравнять ее радиус и минимальный размер зоны Бриллюэна. Найдем концентрацию при условии касания: 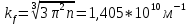 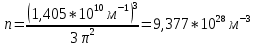 Согласно приближению слабой связи, размер зона Бриллюэна для изотропных кристаллов кубической сингонии составляет 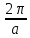 . Для первой зоны Бриллюэна: . Для первой зоны Бриллюэна: 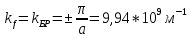 Сравнив полученное значение с размером зоны Бриллюэна, выбранным ранее, можно заключить, что в применение теории свободных электронов возможна: 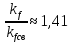 Найдем концентрацию по формуле: 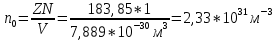 Так как 𝑛0> n, теория свободных электронов неприменима, соответственно нельзя вводить понятие электронного Ферми газа. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||