гидромеханика задачи. гидромеханика. Решение Избыточное давление жидкости в полости цилиндра (1) где плотность жидкости

• Название: Решение Избыточное давление жидкости в полости цилиндра (1) где плотность жидкости
• Анкор: гидромеханика задачи
• Дата: 08.04.2023
• Размер: 297.5 Kb.
• Имя файла: гидромеханика.docx
• Тип: Решение; #1046788
• страница: 2 из 3

Ответ: , .

Задача 24
Конденсатор паровой турбины, установленный на тепловой электростанции, оборудован 8186 охлаждающими трубками диаметром . В нормальных условиях работы через конденсатор пропускается циркуляционной воды с температурой . Будет ли при этом обеспечен турбулентный режим движения в трубках?
Таблица 2 - Исходные данные

Сумма двух последних цифр по номеру зачётной книжки
7	0,02	13700

Решение

Переход от ламинарного режима течения к турбулентному происходит при числе Рейнольдса , которое определяется по формуле:

(1)

где - коэффициент кинематической вязкости воды при , ;

- скорость движения воды, ;

(2)


Подставляя полученное значение в формулу (1), находим

- при



- при


число Рейнольдса больше критического значения , следовательно, режим движения турбулентный.
Ответ: режим движения турбулентный.

Задача 30

На поршень диаметром 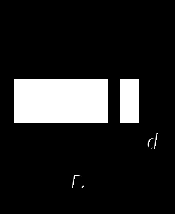действует сила (рисунок 4). Определить скорость движения поршня, если в цилиндре находится воды, диаметр отверстия в поршне , толщина поршня . Силой трения поршня о цилиндр пренебречь, давление жидкости на верхнюю плоскость поршня не учитывать.



Рисунок 4 - Графическое изображение к задаче № 30

Таблица 2 - Исходные данные

Сумма двух последних цифр по номеру зачётной книжки
7		200	12	20

Решение

Гидростатическое давление, создаваемой под поршнем в результате действия силы , равно:

(1)

где - площадь поперечного сечения поршня, ;

(2)

Подставляя выражение (2) в (1), получаем

(3)

Напор над отверстием определяем по формуле:

(4)

Расход воды через отверстие составит:

(5)

где - коэффициент расхода;

Так как в данном случае имеем малое отверстие в тонкой стенке , то коэффициент расхода составляет


Скорость движения поршня в цилиндре:

(6)

Ответ: .


Задача 38
Из напорного бака вода течет по трубе диаметром 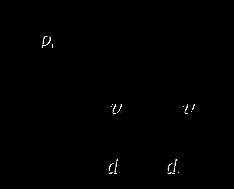и затем вытекает в атмосферу через насадки (брандспойт) с диаметром выходного отверстия . Избыточное давление воздуха в баке ; высота . Пренебрегая потерями энергии, определить скорости течения воды в трубе и на выходе из насадки (рисунок 5).



Рисунок 5 - Графическое изображение к задаче № 38

Таблица 2 - Исходные данные

Сумма двух последних цифр по номеру зачётной книжки
7	18	10	0,18	1,8

Решение

Уравнение Бернулли для элементарной струйки или потока идеальной жидкости имеет вид:

(1)

где - вертикальные координаты центров тяжести сечений (удельная энергия положения), ;

- пьезометрическая высота (удельная энергия давления), ;

- скоростной напор (удельная кинетическая энергия), .

Сечение проводим через свободную поверхность жидкости в резервуаре, сечение проводим через насадок, а плоскость сравнения - по оси трубопровода.

Составляем уравнение Бернулли для сечений и . Учитывая, что ; ; ; ; уравнение Бернулли принимает вид:

(2)

отсюда находим скорость воды на выходе из насадки

(3)

Уравнение расхода представляет собой условие неразрывности (сплошности) потока несжимаемой жидкости:

(4)

где - расход воды через трубопровод, ;

(5)

тогда

(6)

отсюда находим скорость воды в сечении

(7)

где - площади поперечных сечений трубопроводов 1 и 2 соответственно, ;

тогда выражение (7) можно переписать в следующем виде

(8)



Ответ: , .