решение уравнений. Практическая работа №3 Решение уравнений. Решение квадратного уравнения Используется для нахождения корней многочлена второй степени вида f
 Скачать 82.17 Kb. Скачать 82.17 Kb.
|
|
Решение уравнений Решение квадратного уравненияИспользуется для нахождения корней многочлена второй степени вида: f( x)ax2 bxc Порядок выполнения: Вводятся коэффициенты уравнения. Вводится матрица, состоящая из данных коэффициентов, записанных в обратном порядке. Производится еѐ транспонирование. Для нахождения решения используется функция polyroots Пример: Решить квадратное уравнение: x2 2x 8 0 Ввод коэффициентов уравнения.    a 1 b 2 c 8 a 1 b 2 c 8Вводится матрица, состоящая из коэффициентов, записанных в об- ратном порядке. Производится еѐ транспонирование.  v ( c b a ) T v ( c b a ) TДля нахождения решения используется функция polyroots.   2 2 r polyroots(v) r = r polyroots(v) r =4 Символьное решение уравненийПорядок выполнения: Ввести уравнение. Синим уголком курсора выделить переменную, относительно которой нужно решить уравнение. В главном меню выбрать команду Symbolics→Variable→Solve (Символьныевычисления→Переменная→Решить). Пример: Символьно найти решение уравнения относительно переменной h: 2h3 h b 0 Ввод уравнения. В качестве знака равно использовать знак Булева ра- венства (вводится сочетанием клавиш [Ctrl]+[=]).  2h2 h b 0 2h2 h b 0Выделение переменной, относительно которой проводится решение. Решение уравнения при помощи команды Symbolics → Variable → Solve (Символьные вычисления → Переменная → Решить).   8b 1 1 8b 1 1 4  8b 1 8b 14 4 1  4 4 Недостаток использования меню Symbolics заключается в том, что най- денное решение не пересчитывается автоматически при изменении выражения или входящих в него величин и не участвует в последующих расчетах. Достоинством использования меню Symbolics является то, что ранее принятые численные значения величин не учитываются в символьных расчетах. Если выделенное выражение не имеет символьного решения (а большин- ство уравнений не имеет символьного решения), то Mathcad сообщает об ошибке: «No solution was found» («Решение не найдено»). Численное решение уравненийФункция root решает уравнения итерационным методом секущих и по- этому требует задания перед собой начальных значений. Кроме того, функция root, выполняя вычисления методом спуска, находит и выводит только один ко- рень, ближайший к начальному приближению. Для поиска остальных корней уравнения необходимо задание других начальных значений. Пример: Найти корни уравнения в диапазоне от -4 до 3: x3 6x 2 0 Ввод диапазона, где определяется корень.  x 4.. 3 x 4.. 3 Ввод уравнения. Ввод уравнения.  f( x) f( x)x3 6.x 2  Поиск интервалов, где происходит смена знака функции. Поиск интервалов, где происходит смена знака функции.
x f (x) Данных интервалов 3 (-3…-2, 0…1, 2..3), следовательно уравнение на заданном интервале имеет 3 корня. Задание точности вычисления корня.  TOL 10 5 TOL 10 5Задание начального положения для поиска. Задается как среднее зна- чение между значениями переменной, где происходит смена знака функции.  x 3 2 x 3 22 x 2.5 Вычисление корня X1 root (f (x) x) X1 2.602 Проверка решения. Значение функции должно быть близко к 0. f (X1) 3.553 15 10 Вычисление второго корня.  x 0 1 x 0 12 X2 root (f (x) x) f (X2) 6.095 11 x 0.5 X2 0.34 10 Вычисление третьего корня  x 2 3 x 2 32 X3 root (f (x) x) 10 f (X3) 3.052 10 x 2.5 X3 2.262 Поиск экстремума функцииС помощью функции root можно найти и экстремум функции, приравняв производную к нулю. Функции должно предшествовать начальное приближение. Для нахождения экстремума функции следует: Задать начальное приближение, наиболее близко расположенное к экстремуму. Для его поиска необходимо определить, на каких интервалах проис- ходит смена знака производной функции. Записать выражение с функцией root, включив в качестве функции, которая должна быть равна нулю, производную по заданной переменной; Вычислить значение заданной функции от найденного корня. Пример: Найти экстремумы уравнения в диапазоне от -4 до 3: x3 6x 2 0 Ввод диапазона.  x 4.. 3 x 4.. 3 Ввод уравнения. Ввод уравнения.  f( x) f( x)x3 6.x 2  Поиск интервалов, где происходит смена знака производной функции Поиск интервалов, где происходит смена знака производной функции d f (x) d f (x)
x dx Данных интервалов 2 (-2…-1, 1…2), следовательно уравнение на заданном диапазоне имеет 2 экстремума. Задание точности вычисления экстремума.  TOL 10 5 TOL 10 5Задание начального положения для поиска экстремума. Задается как среднее значение между значениями переменной, где происходит смена знака градиента функции.  x 2 1 x 2 12 x 1.5 Нахождение первого экстремума X1 root d f (x) x X1 1.414 dx Вычисление значения функции в экстремуме. f (X1) 7.657 Нахождение второго экстремума.  x 1 2 x 1 22 X2 root d f (x) x x 1.5 X2 1.414 dx f (X2) 3.657 Решение систем линейных алгебраических уравненийИзвестно, что система линейных уравнений в матричной форме A∙X=B. Вектор решения получается из X=A-1∙B. Для решения систем линейных уравнений в MathCAD существует встро- енная функция lsolve(A,B), которая возвращает вектор X для системы линейных уравнений при заданной матрице коэффициентов и векторе свободных членов. Также используются системы линейных уравнений для вычисления оп- ределителя по формулам Крамера – точный метод решения. Решение линейной системы методом Гаусса – приближенный метод. Функции, предназначенные для решения задач линейной алгебры, можно разделить на три группы: функции определения матриц и операции с блоками матриц; функции вычисления различных числовых характеристик матриц; функций, реализующие численные алгоритмы решения задач линейной алгебры. Пример: Решить систему линейных уравнений: x2 y3z1 2 x3 y z2 x2 y5z3 Преобразуем данную систему: 1x2 y3z1 2 x3 y1z2 1x2 y5z3 Матрица коэффициентов системы:   1 2 3 1 2 3 A 2 3 1 A 2 3 11 2 5 Вектор свободных членов   1 1 b 2 b 23 Решение системы   X A 1.b X A 1.bРезультаты решения  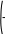 8 8X = 5 1 Проверка решения   0 0 A.X b = 0 A.X b = 00 Решение с применением функции Isolve   X lsolve( A, b) X lsolve( A, b) 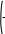 8 8X = 5 1 Решение системы линейных уравнений по формулам КрамераПорядок выполнения Переменной ORIGIN присвоить значение равное единице. Ввести матрицу коэффициентов системы. Ввести вектор свободных членов (столбец правых частей). Вычислить определитель матрицы системы. Система имеет единст- венное решение, если определитель отличен от нуля. Вычислить определителей матрицы, полученных заменой соот- ветствующего столбца столбцом правых частей. Определить решение системы по формулам Крамера. Пример: Решить систему линейных уравнений: x2 y3z1 2 x3 y z2 x2 y5z3 Преобразуем данную систему: 1x2 y3z1 2 x3 y1z2 1x2 y5z3 Матрица коэффициентов системы:   1 2 3 1 2 3 A 2 3 1 A 2 3 11 2 5 Вектор свободных членов   1 1 b 2 b 23 Присваиваем переменной ORIGIN значение 1.  ORIGIN 1 ORIGIN 1Вычисляем определителя матрицы системы.     A = 2 A = 2Вычисление определителей матрицы  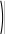 1 2 3 1 2 3 1 2 3 1 1 2 3 13 2 5 1 1 3  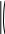 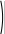 2 2 2 1 2 2 2 11 3 5 1 2 1  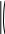 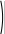 3 2 3 2 3 2 3 21 2 3  1 = 16 1 = 162 = 10 3 = 2  Определение решения системы по формулам Крамера Определение решения системы по формулам Крамера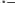 x 1 x 1 y 2   z 3  x = 8 y = 5 z = 1 Решение линейной системы методом Гаусса (метод гауссовых ис- ключений)Порядок выполнения: Переменной ORIGIN присвоить значение равное единице. Ввести матрицу системы и вектор-столбец правых частей. Сформировать расширенную матрицу системы при помощи функции augment(A,b).Привести расширенную матрицу системы к ступенчатому виду при помощи функции rref(Ar). Сформировать столбец решений системы при помощи функции sub- matrix(Ag,1,3,4,4). Пример: Решить систему линейных уравнений: x2 y3z1 2 x3 y z2 x2 y5z3 Преобразуем данную систему: 1x2 y3z1 2 x3 y1z2 1x2 y5z3 Матрица коэффициентов системы:   1 2 3 1 2 3 A 2 3 1 A 2 3 11 2 5 Вектор свободных членов   1 1 b 2 b 23 Присваиваем переменной ORIGIN значение 1.  ORIGIN 1 ORIGIN 1Формирование расширенной матрицы системы  Ar augment(A, b) Ar augment(A, b)Ar = 1 2 3 1   2 3 1 2 2 3 1 21 2 5 3 Приведение расширенной матрицы системы к ступенчатому виду  Ag rref( Ar ) Ag rref( Ar )Ag = 1 0 0 8    0 1 0 5 0 1 0 50 0 1 1 Формирование столбца решения системы   8 8  x submatrix( Ag , 1, 3, 4, 4) x submatrix( Ag , 1, 3, 4, 4)x = 5 1 Решения нелинейных уравненийРешение трансцендентных уравнений Многие уравнения, например трансцендентные, не имеют аналитических решений. Однако они могут решаться численными методами с заданной по- грешностью. Для простейших уравнений вида F(x)=0 решение находится с по- мощью функции root. Эта функция возвращает значение переменной с указан- ным уровнем, при котором выражение дает 0. Пример: Решить уравнение 3-ей степени: x3 6x2 21x 52 0 Ввод коэффициентов полинома.     a3 1 a2 6 a1 21 a0 52 a3 1 a2 6 a1 21 a0 52  Ввод полинома. Ввод полинома.  f(x) f(x)a3.x3 a2.x2 a1.x a0  Вычисление действительного корня с помощью функции root. Вычисление действительного корня с помощью функции root.   x 0 x1 root( f( x), x) x1= 4 x 0 x1 root( f( x), x) x1= 4Вычисление двух других корней. 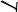   i 1 x 1 i 1 x 11.i  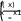 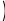 x2 root , x x2 root , x 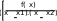 x3 root x3 rootx2= 1 +3.464i   , x x3= 1 3.464i , x x3= 1 3.464iРешение систем нелинейных уравнений при помощи блока «Giv- en – Find»При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом – директивой Given – и имеющий следующую структуру: Ввод начальных приближений GivenУравнения Выражения с функциями find и minerr Пример: Решить систему нелинейных уравнений: 2 x y5 z2 y3 4 z4 xy zez Задание начальных приближений для всех неизвестных.    x 1 y 1 z 0 x 1 y 1 z 0Ввод уравнений в блок решения уравнения. Given   y 5 y 5  z2 z2  y3 4.z 4 y3 4.z 4    z ez z ez vec find( x, y, z) vec find( x, y, z)Найденное решение.   1.325 1.325vec = 1.823 0.513 Символьное решение систем уравненийнужно: Для того, чтобы найти решение системы уравнений в символьном виде, Ввести слово Given. Ввести уравнения и неравенства ниже слова Given. Ввести функцию Find с аргументами-неизвестными. Убедиться в том, что команда Использоватьсимволикув меню Ма- тематикаотмечена галочкой, в противном случае выберите эту команду. Ввести комбинацию клавиш [Ctrl]+[+]. Mathcad выводит стрелку вправо. Щѐлкнуть вне области действия функции Find. Mathcad вырабатыва- ет результат в виде вектора. Результаты размещаются в том же порядке, в кото- ром были перечислены неизвестные-аргументы функции Find. Пример: Найти координаты точки пересечения 2-х прямых: x2 ya 4 x yb Ввод уравнений в блок решения уравнения Given    x 2..y a x 2..y a  4.x y b 4.x y bНайденное решение.  1 1  .( 2..b a) .( 2..b a)  Find( x, y) Find( x, y)( 1 8.) ( 4.a b) ( 1 8.) |
