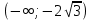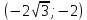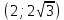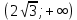зад 1-8. Занятие 3 Темы Введение в математический анализ. Дифференциальное исчисление функции одной переменной. Интегральное исчисление функции одной переменной. Элементы линейной алгебры. Основы теории комплексных чисел. Основы математической статистики
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Практическое занятие 3 Темы: Введение в математический анализ. Дифференциальное исчисление функции одной переменной. Интегральное исчисление функции одной переменной. Элементы линейной алгебры. Основы теории комплексных чисел. Основы математической статистики. Цель занятия: овладеть навыками вычисления пределов функции в точке и на бесконечности; овладеть навыками решения задач дифференциального исчисления; овладеть навыками решения задач интегрального исчислении; овладеть навыками решения простейших задач линейной алгебры; научиться выполнять действия над комплексными числами, представленными в алгебраической форме; овладеть навыками решения простейших статистических задач. Задание 1. (Максимальное количество баллов – 2 балла) Вычислите пределы функции, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): a) 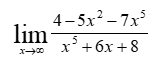 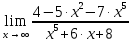 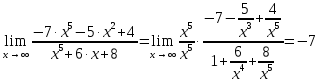 b) 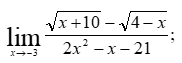 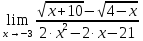 Для выражения 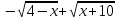 сопряженным является 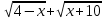 Умножим его на числитель и знаменатель. 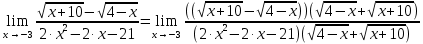 Учитывая, что (a-b)(a+b) = a2-b2, получаем: 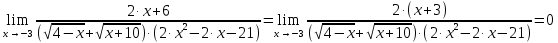 Ответ: 0 Задание 2. (Максимальное количество баллов – 2 балла) Вычислите производные функций, подробно описывая ход решения (указывайте формулы, которыми пользуетесь при решении, записывайте промежуточные результаты): a) 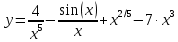 Решение: 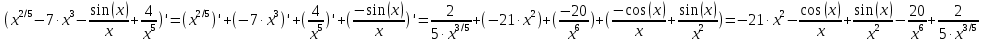 Производную этого выражения находим по формуле: (xn)' = n∙xn-1 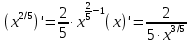 (x)' = 1 Здесь: (-7∙x3)' = -7∙3∙x3-1(x)' = -21∙x2 (x)' = 1 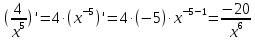 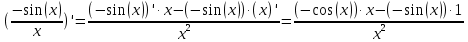 (sin(x))' = cos(x) Ответ: 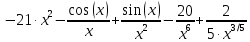 При вычислении были использованы следующие правила дифференцирования: (xa)' = axa-1 (a)' = 0 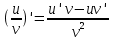 b) Решение: 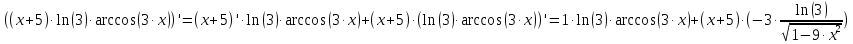 Здесь: 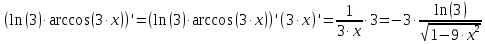 (3∙x)' = 3 Ответ: 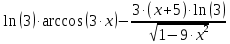 При вычислении были использованы следующие правила дифференцирования: (xa)' = axa-1 (a)' = 0 (uv)' = u'v + uv' (f(g(x)))' = f(x)'∙g(x)' Задание 3. (Максимальное количество баллов - 4 балла) Вам предложена функция 1. Найти область определения функции. 2. Найти точки пересечения с осями. 3. Исследовать функцию на четность/нечетность. 4. Найти асимптоты. 5. Найти экстремумы и интервалы монотонности функции. 6. Найти интервалы выпуклости функции и точки перегиба. 7. Найти дополнительные точки, уточняющие график. 8. Построить график. 1) Область определения функции. Точки разрыва функции. D(y)=R, но х≠±2 2) Четность или нечетность функции. 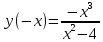 y(-x) = -y(x), нечетная функция 3) Периодичность функции. 4) Точки пересечения кривой с осями координат. Пересечение с осью 0Y x=0, y=0 Пересечение с осью 0X y=0 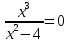 x1=0 5) Исследование на экстремум. y = x^3/(x^2-4) Найдем точки разрыва функции. x1 = 2 x2 = -2 Поскольку f(-x)=-f(x), то функция является нечетной. 1. Находим интервалы возрастания и убывания. Первая производная. 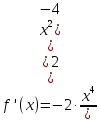 или 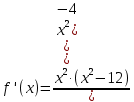 Находим нули функции. Для этого приравниваем производную к нулю x2∙(x2-12) = 0 Откуда: x1 = 0 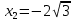 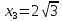
В окрестности точки x = -2∙sqrt(3) производная функции меняет знак с (+) на (-). Следовательно, точка x = -2∙sqrt(3) - точка максимума. В окрестности точки x = 2∙sqrt(3) производная функции меняет знак с (-) на (+). Следовательно, точка x = 2∙sqrt(3) - точка минимума. 2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. 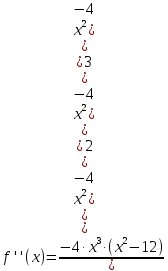 или 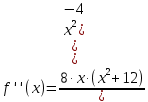 Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 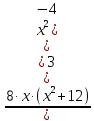 Откуда точки перегиба: x1 = 0
6) Асимптоты кривой. 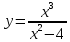 Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 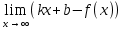 Находим коэффициент k: 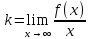 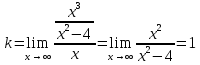 Находим коэффициент b: 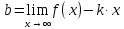 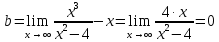 Получаем уравнение наклонной асимптоты: y = x Найдем вертикальные асимптоты. Для этого определим точки разрыва: x1 = -2 x2 = 2 Находим переделы в точке x=-2 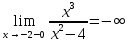 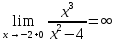 x1 = -2 - точка разрыва II рода и является вертикальной асимптотой. Находим переделы в точке x=2 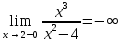 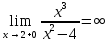 x2 = 2 - точка разрыва II рода и является вертикальной асимптотой. 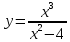 Найдем наклонную асимптоту при x → -∞: 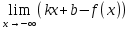 Находим коэффициент k: 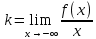 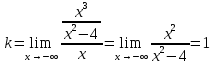 Находим коэффициент b: 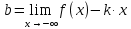 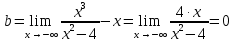 Получаем уравнение наклонной асимптоты: y = x 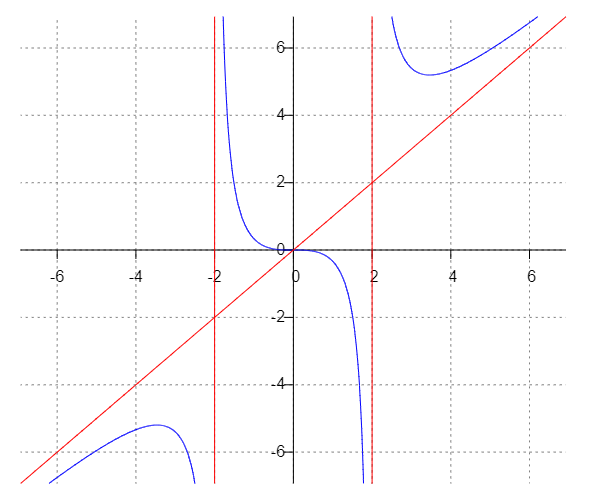 Задание 4. (Максимальное количество баллов – 2 балл) Вычислите неопределенные интегралы: a) 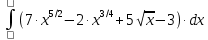 Представим исходный интеграл, как сумму табличных интегралов: 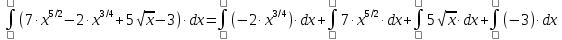 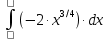 Это табличный интеграл: 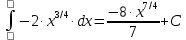 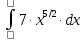 Это табличный интеграл: 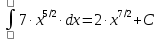 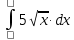 Это табличный интеграл: 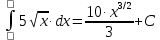 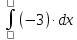 Это табличный интеграл: 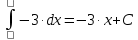 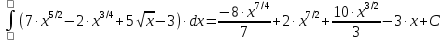 b) 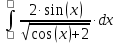 Выражение -sin(x) подведем под знак дифференциала, т.е.: (-sin(x))∙dx = d(cos(x)), t=cos(x) Тогда исходный интеграл можно записать так: 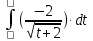 Это табличный интеграл: 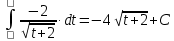 Чтобы записать окончательный ответ, осталось вместо t подставить cos(x). 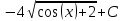 Задание 5. (Максимальное количество баллов – 4 балла) Вычислите площадь фигуры, ограниченной графиками функций f(x) и g(x), подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): 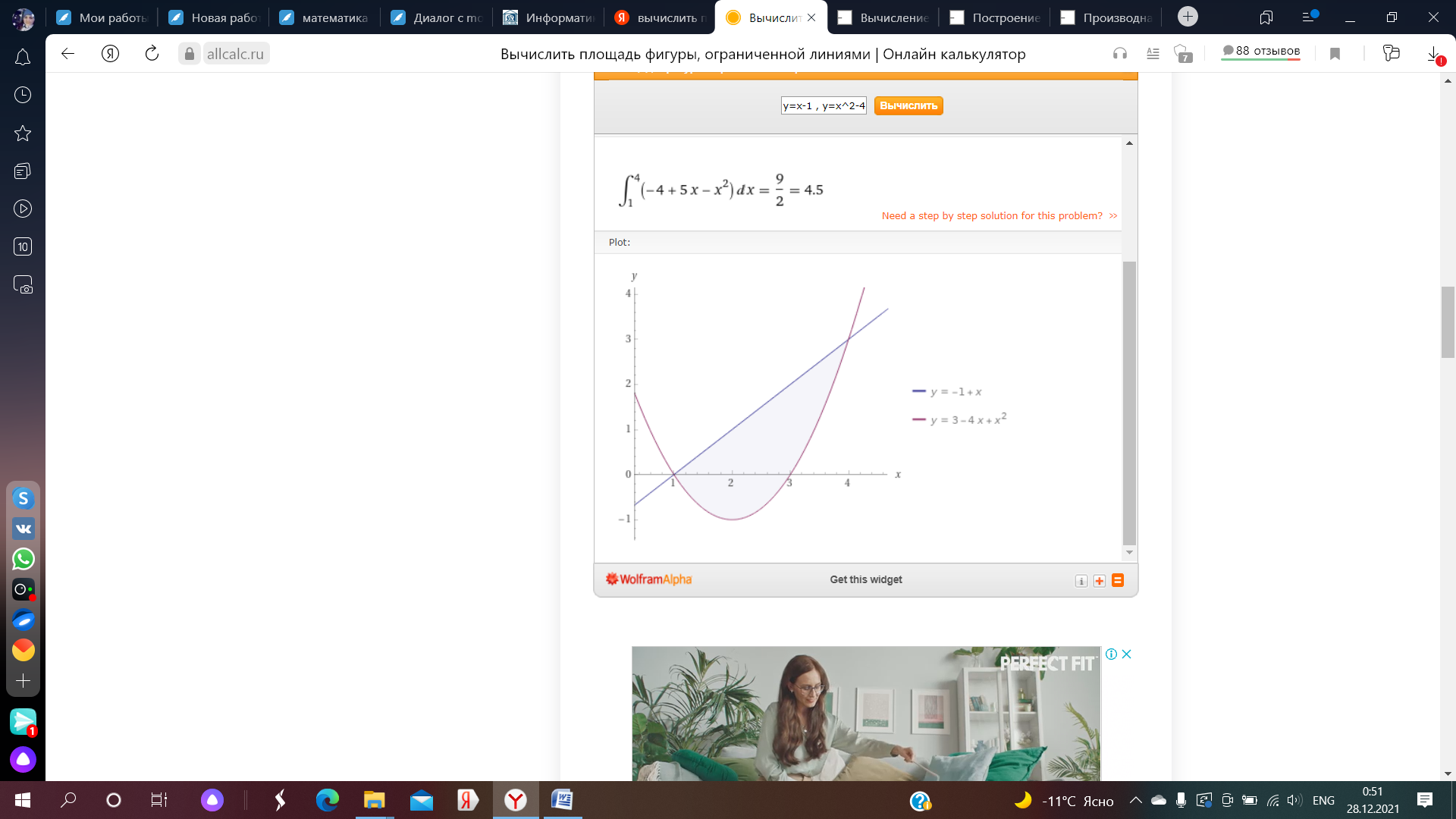 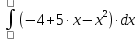 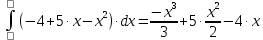 Вычислим определенный интеграл: 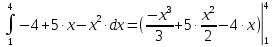 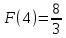 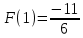 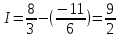 Задание 6. (Максимальное количество баллов – 3 балла) Решите систему линейных уравнений методом Крамера, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): 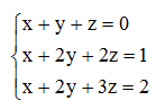 Запишем систему в виде: BT = (0,1,2) Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю. Определитель: ∆ = 1*(2*3-2*2)-1*(1*3-2*1)+1*(1*2-2*1) = 1 Заменим 1-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 0*(2*3-2*2)-1*(1*3-2*1)+2*(1*2-2*1) = -1 Заменим 2-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 1*(1*3-2*2)-1*(0*3-2*1)+1*(0*2-1*1) = 0 Заменим 3-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 1*(2*2-2*1)-1*(1*2-2*0)+1*(1*1-2*0) = 1 Выпишем отдельно найденные переменные Х Проверка. 1*(-1)+1*0+1*1 = 0 1*(-1)+2*0+2*1 = 1 1*(-1)+2*0+3*1 = 2 Задание 7. (Максимальное количество баллов – 3 балла) Найдите модуль и аргумент комплексного числа z = 3 + 3i Изобразите комплексное число на плоскости, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты). Запишите полученное число в тригонометрической и показательной формах. 1. Находим тригонометрическую форму комплексного числа z = 3+I*3 Действительная часть числа x. x = Re(z) = 3 Мнимая часть числа y. y = Im(z) = 3 Модуль комплексного числа |z|. Поскольку x > 0, y > 0, то arg(z) находим как: Таким образом, тригонометрическая форма комплексного числа z = 3+I*3 2. Находим показательную форму комплексного числа z = 3+I*3 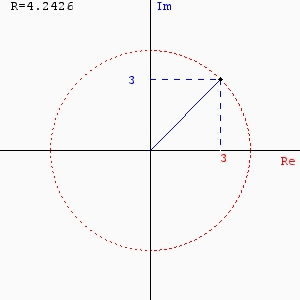 Задание 8. (Максимальное количество баллов – 5 баллов) Изучите предложенные исходные данные, полученные при измерении:
Выполните задания с учетом исходных данных, подробно описывая ход вашего решения: a) Построить полигон распределения. b) Вычислить выборочную среднюю, дисперсию, моду, медиану. c) Найти коэффициент вариации и сделать выводы Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.
Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. Имеются два показателя с одинаковым значением частоты f=3. Ряд имеет две моды, т.е. является бимодальным. Медиана. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 6. Это значение xi = 4. Таким образом, медиана равна 4. Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных. В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср-Me) ≈ xср-Mo Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 5 - 1 = 4 Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 1.44 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). = или = Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 3.3 в среднем на 1.552 Оценка среднеквадратического отклонения. Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v>30% ,но v<70%, то вариация умеренная. Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины. Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. Выводы: Каждое значение ряда отличается от среднего значения 3.3 в среднем на 1.552. Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная. 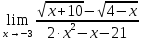 Для выражения 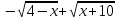 сопряженным является 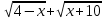 Умножим его на числитель и знаменатель. 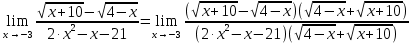 Учитывая, что (a-b)(a+b) = a2-b2, получаем: 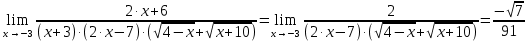 Ответ: 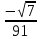 |