Раздел долгосрочного плана: 10.3А Предел функции и непрерывность
|
Школа: ГУ Архиповская средняя школа
|
Дата:
|
ФИО учителя: Гудова Л.В
|
Класс: 10
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Вычисление пределов функций. Первый замечательный предел.
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
10.5.1.14 знает определение и свойства предела функции;
10.5.1.15 вычисляет пределы функций на бесконечности и в точке;
10.5.1.16 знает и применяет первый замечательный предел.
|
Цели урока
|
Использует правила вычисления пределов на бесконечности и в точке, знает способы избавления от неопределённостей при вычислении пределов. Знает первый замечательный предел и использует его для вычисления пределов.
|
Критерии успеха
|
Ученик достиг цели, если:
- знает правила вычисления пределов на бесконечности и применяет их;
- знает правила вычисления пределов в точке и применяет их;
- знает способы избавления от различных видов неопределённостей, использует их для вычисления пределов;
- знает первый замечательный предел;
- с помощью тригонометрических формул проводит преобразования выражений, стоящих под знаком предела;
- вычисляет пределы.
|
Языковые цели
|
Учащиеся будут:
описывать поведение функции в окрестности фиксированной точки;
комментировать нахождение асимптот;
объяснять вычисление пределов функций;
обсуждать методы раскрытия неопределенностей.
Предметная лексика и терминология:
предел функции;
непрерывность функции в точке;
непрерывность функции на множестве;
точки разрыва;
вертикальная асимптота;
наклонная асимптота;
горизонтальная асимптота;
вид неопределенности;
первый замечательный предел.
Серияполезных фраз для диалога/письма:
чтобы найти ...асимптоту, надо …;
для раскрытия неопределенности вида …, надо …;
чтобы вычислить значение предела данной функции в точке, надо …;
первый замечательный предел применяется ...;
для исследования функции на непрерывность, надо ….
|
Привитие ценностей
|
Академическая честность, ответственное отношение к своим обязанностям в коллективе, терпимое отношение к мнению коллектива, толерантность.
Знание и понимание ГГ: устойчивое развитие, социальная справедливость и равенство.
Ценности ГГ: целенаправленное участие и вовлеченность.
Навыки ГГ: критическое и творческое мышление, уверенность в себе и навыки рефлексии, общение.
|
Межпредметные связи
|
Английский язык, физика, биология.
|
Навыки использования ИКТ
|
Использование возможностей интерактивной доски, возможностей образовательного ресурса bilimland.kz
|
Предварительные знания
|
Понятие бесконечности, предела функции в точке и на бесконечности. Правила вычисления пределов функции в точке и на бесконечности, способы раскрытия неопределённости, тригонометрические формулы.
|
Ход урока
|
Запланиро-ванные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
3 мин
|
Совместное определение целей урока, повторение правил вычисления пределов на бесконечности и в точке.
|
https://azbyka.ru/deti/logicheskie-i-zanimatelnye-zadachi
|
Середина урока
60 мин
15 мин
|
Изучение нового материала
При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределенностями.
Основные виды неопределенностей:
 , , 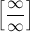 , , 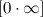 , ,  , , 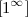 , , 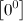 , , 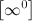
Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.
Для раскрытия неопределенностей используют следующие способы:
1.раскладывают на множители,
2. преобразуют функцию с помощью формул сокращенного умножения,
3. преобразуют функцию с помощьютригонометрических формул,
4.домножают на сопряженное,
что позволяет в дальнейшем сократить выражение и т.д., и т.п.;
Разберём отдельные примеры раскрытия неопределённостей.
Пример: Видео 1 (слайд 3)
1. Предел частного многочленов на бесконечности:

Пример:
Найти предел 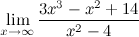 . .
Решение:
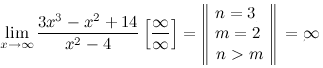

2. Предел целой рациональной функции:
Если  , то , то  . .
Пример:Найти предел функции  в точке в точке 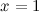 . .
Решение:  . .
3. Пределы иррациональных выражений:
а.чтобы найти предел дроби, содержащей иррациональное выражение в случае, когда предел и числителя, и знаменателя равен нулю, надо перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель и после этого сделать необходимые упрощения. Иррациональность переносится с помощью домножения и числителя и знаменателя дроби на выражение, сопряженное к иррациональности.
Пример:Вычислить предел 
Решение: Получим неопределенность и домножим числитель и знаменатель на выражение, сопряженное к иррациональности.
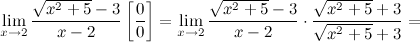




б.Вычисление пределов, содержащих разность корней:
Пример: Вычислить предел 
Решение: Получим неопределенность и домножим и поделим выражение на сопряженное.





4. Раскрытие неопределенности  в частном двух многочленов с помощью разложения на множители: в частном двух многочленов с помощью разложения на множители:
Пример: Вычислить предел 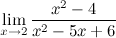
Решение: Получим неопределенность, разложим на множители числитель и знаменатель, сократим одинаковые элементы.



Закрепление изученного материала
№1.Найти пределы:
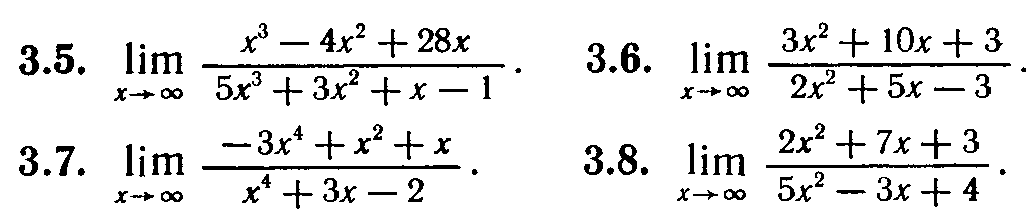


№2. Найти пределы:


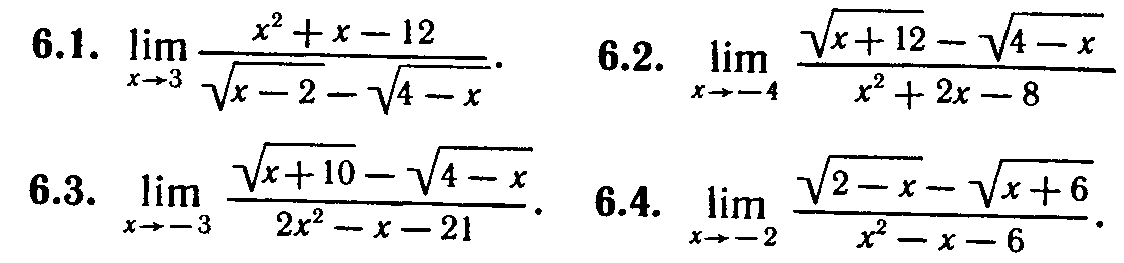

Найти пределы:
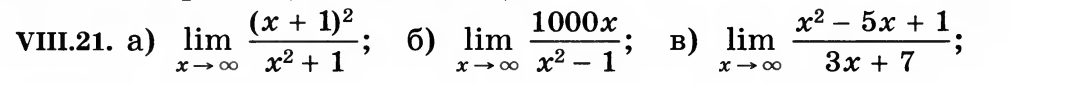


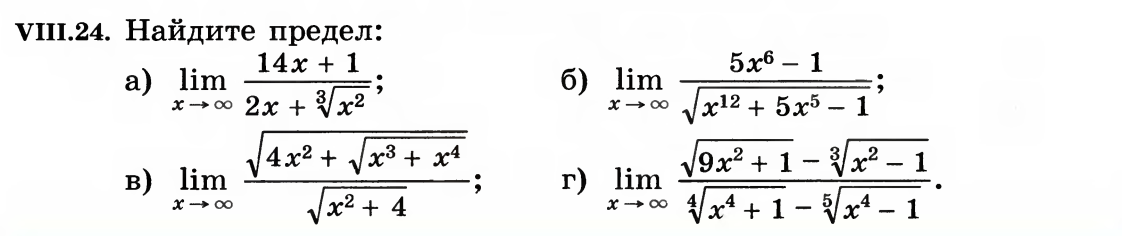
Изучение нового материала
Первый замечательный предел

Определение: Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Пример 0: Видео2 (в нём речь идёт и о втором замечательном пределе, эту часть видео можно продемонстрировать ученикам в качестве дополнительного материала, слайд 3).
Пример1:Найти предел 
Решение: Воспользуемся заменой и первым замечательным пределом.
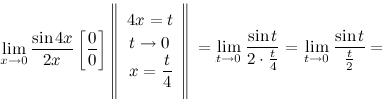
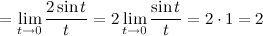
Пример 2:Найти предел 
Решение: Разложим тангенс на синус и косинус и воспользуемся
свойствами пределов.



Пример 3:Вычислить предел 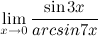
Решение: Получим неопределенность, сделаем замену.
При 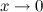 : :  , , 

Следствия из первого замечательного предела
1° 
2° 
3° 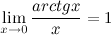
4° 
Закрепление изученного материала
Вычислите пределы:
1. 
|
2. 
|
3. 
|
4. 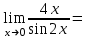
|
5. 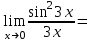
|
6. 
|
7. 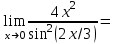
|
8. 
|
9. 
|
10. 
|
11. 
|
|

2.18
 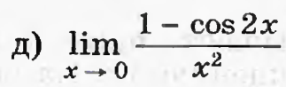
Вычислите пределы:

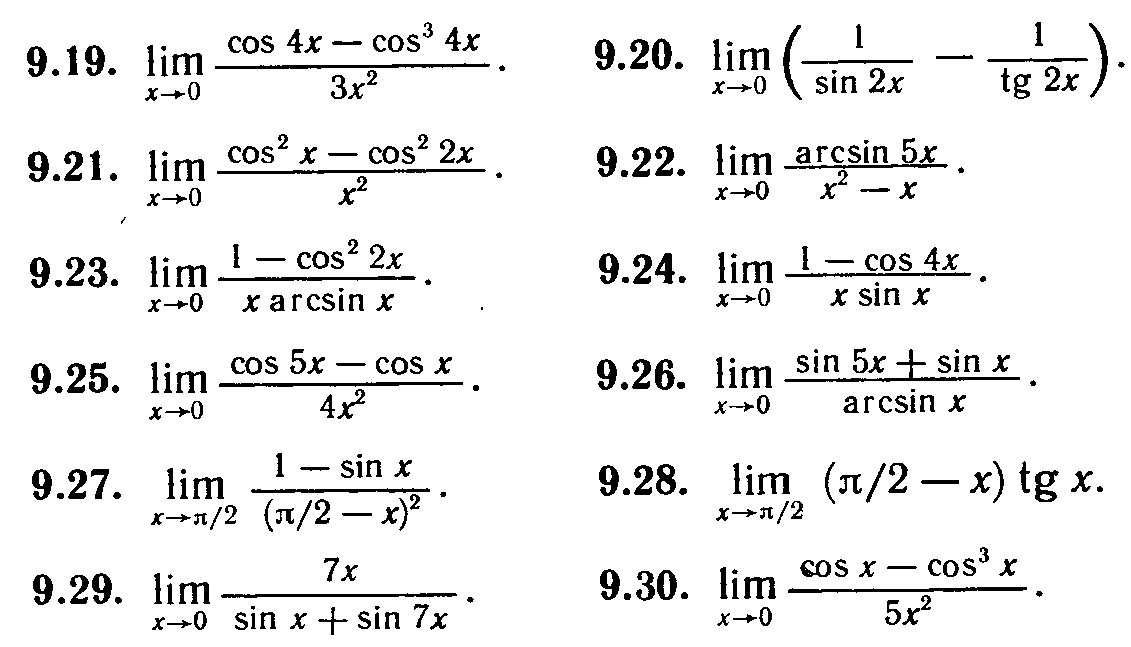
ФОиз 2 вариантов:

|
bilimland.kz
Мордкович А.Г. «Алгебра и начала анализа, 10 класс, часть1 (профильный уровень)» / Москва, «Мнемозина», 2009 г.
Рябушко А.П. «Сборник ИЗ по высшей математике»
|
Конец урока
1 мин
|
Рефлексия:

|
3 факта, которые вы сегодня узнали …
2 формы работы, которые вам понравились …
1 вопрос, который у вас остался …
|
|
|
1 мин
|
Домашнее задание:
Вычислите пределы:
1. 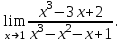 2. 2. 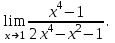

3.
4. 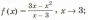
5.
6.

|
|
Дополнительная информация
|
Дифференциация - как вы планируете оказывать больше поддержки? Как вы планируете давать задания более способным учащимся?
|
Междисциплинарные связи
Безопасность жизнедеятельности
ИКТ связи
Связи с ценностями
|
|
|
Оценивание - как вы планируете проверить знания учащихся?
|
|
Используйте графу ниже, чтобы проанализировать Ваш урок. Ответьте на самые актуальные вопросы о проведенном уроке.
|
|
Сводная оценка
Какие два аспекта прошли очень хорошо (рассмотрите преподавание и обучение)?
1:
2:
Какие два аспекта улучшили бы урок (рассмотрите преподавание и обучение)?
1:
2:
Что я узнал о классе или об отдельных учащихся на данном уроке, что я учту на следующем уроке?
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb.