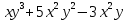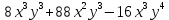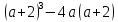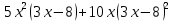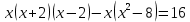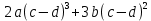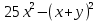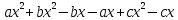Выступление. Тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения (закрепление материала)

• Название: Тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения (закрепление материала)
• Анкор: Выступление
• Дата: 10.03.2023
• Размер: 41.33 Kb.
• Имя файла: urok.docx
• Тип: Урок; #978505

Краткосрочный план

7.3B: Формулы сокращенного умножения	Школа: КГУ «СОШ № 10»
Дата:	ФИО учителя: Рыжова И.А.
Класс: 7Б	Количество присутствующих: 19	отсутствующих:0
Тема урока:	Тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения (закрепление материала)
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)	7.2.1.15 выполнять тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения
Цели урока	выполняет тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения
Критерии оценивания	умеет выполнять тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения
Языковые цели	Будут: давать словесную формулировку формул сокращённого умножения; записывать формулы сокращенного умножения по словесной формулировке; аргументировать выбор способа разложения многочлена на множители; объяснять выполнение разложения многочлена на множители. Лексика и терминология, специфичная для предмета: формулы сокращенного умножения; разность квадратов двух выражений; квадрат суммы двух выражений; квадрат разности двух выражений; удвоенное произведение; утроенное произведение; куб суммы двух выражений; куб разности двух выражений; сумма кубов двух выражений разность кубов двух выражений; разложение на множители; общий множитель; наибольший общий множитель; способ группировки; полный квадрат; неполный квадрат.
Привитие ценностей	Уважение, сотрудничество, открытость. Привитие ценностей осуществляется через парную и групповую виды работ.
Межпредметные связи	арифметика
Навыки использования ИКТ
Предварительные знания	Знает свойства степени с натуральным показателем. Умение выполнять действия с одночленами и многочленами.

Запланированные этапы урока	Виды упражнений, запланированных на урок:		Ресурсы
Начало урока. 12 мин	1. Организационный момент. Приветствие, проверка отсутствующих и готовности учащихся по домашнему заданию. 2.Психологический настрой на урок. Использование стратегии «Мы - уникальные». Точно следуя инструкциям учителя, ученикам предлагается взять листок бумаги, изобразить цветок из четырех лепестков, при этом раскрасить его с помощью предложенных карандашей. После чего учитель предлагает посмотреть на рисунки других. Есть ли учащиеся с одинаковыми цветками? Нет! Значит, все мы уникальны и индивидуально мыслим. Оценивание: «Похвала» 3. Постановка темы и цели урока. Использование стратегии «Уберите лишнее» На доске представлены пять слов (приводящие к теме урока). Учащимся необходимо убрать лишнее слова не имеющее отношение к другим. По оставшимся словам необходимо определить тему и цель урока Равенство, формулы, подобные, множители, сокращение Оценивание: «Уточняющий вопрос» (Каким, словом можно объединить эти слова?) 4. Актуализация знаний Использование стратегии «Тест». Дифференцированный подход, способ «Темп» Учащимся предлагается карта урока, в приложении № 1 указан «Тест», где необходима, выбрать правильный ответ. Тестовое задание на соответствие Вариант 1 1. (4у-3х)(3х+4у)  а. (x+2)(x2-2x+4) 2. 100m 4-4n6  б. (0.2x+1)2 3. (3x+a)2 в.  a3-0.027 4. х³+8  г. a2-10a+25 5. (3х+1)³ д. 9-a2 6. 0,04х2 + 0,4х + 1 е. (10m2-2n3) (10m2+2n3) 7. (а-0,3)(а²+0,3а+0,09)  ж. 9x2+6ax+a2 8. (а  –  5)2  з. 16y2-9x2 9. (3-а)(3+а)  и. 27x3+27x2+9x +1 Вариант 2 1. (3х+1)³  А.16y2-9x2 2. х³+8  Б.(10m2-2n3) (10m2+2n3) 3. (а  –  5)2  В. 9x2+6ax+a2 4. 0,04х2 + 0,4х + 1  Г.(x+2)(x2-2x+4) 5. (4у-3х)(3х+4у)  Д.27x3+27x2+9x +1 6. 100m 4-4n6  Е.(0.2x+1)2 7. (3-а)(3+а)  Ж. a3-0.027 8. (3x+a)2  З. a2-10a+25 9. (а-0,3)(а²+0,3а+0,09) И. 9-a2 Оценивание: обменялись тетрадями по парте и провели оценивание, «Сравнение с образцом». На доске выводятся правильные ответы. «В чем проблема?»: - Что помешала тебе достичь успеха?		Учитель раздает участникам листочки и карандаши (красный, синий, желтый). Доска, мел Тест Приложение №1. доска Ключ 1В: 1з;2е; 3ж;4а;5и 6б, 7в,8г,9д. 2В: 1Д;2Г;3З;4Е;5А 6Б,7И,8В,9Ж
Середина урока.15 мин 10 мин	5. Закрепление. Использование стратегии «Jigsaw» Учащиеся объединяются по четыре, у каждого пронумерованно задание и возможность пользоваться ресурсами (учебник, конспект, помощь учителя). Задание_1'>А уровень Задание 1 Упростите выражения и найдите их значения: a) 27𝑏3 + 27𝑏2𝑎 + 12𝑏𝑎2 + 𝑎3, если 𝑎 = 2; 𝑏 = 1 d) 𝑎3 + 9 − (𝑎 + 1)(𝑎2 − 𝑎 + 1), если 𝑎 = 1 Дескриптор Обучающийся - использует необходимую формулу; - выполняет преобразование выражения; - находит значение. В уровень Задание 2 Разложите на множители: a) (𝑎 − 𝑏)(𝑎2 − 𝑐2) − (𝑎 − 𝑐)(𝑎2 − 𝑏2) b) c) (𝑥 + 𝑦)2 − 10(х2 − у2)+25(𝑥 − 𝑦)2 Дескриптор Обучающийся - выбирает необходимую формулу; - выполняет преобразование; - раскладывает многочлен на множители. С уровень Задание 3 Докажите тождество: a)𝑎3 + 𝑏3 + 3𝑎𝑏(𝑎 + 𝑏) = (𝑎 + 𝑏)3 b) (𝑐 + 𝑑)2(с − 𝑑) + 6𝑐𝑑(𝑐 − 𝑑) + 10𝑐𝑑(𝑑 − 𝑐) = (𝑐 − 𝑑)3 Дескриптор Обучающийся - использует ФСУ; - выполняет преобразования; - доказывает тождество. Вначале учащийся индивидуально работает по своему заданию в своей группе (решает, анализирует и составляет алгоритм решения). После чего учащиеся объединяются в мини группы со своей нумерацией. Создаются экспертные группы. То есть, в первой группе окажутся все те, кто получил задание № 1, во второй — все те, кто получил задание № 2 и т.д. На этом этапе учащиеся обсуждают и выбирают правильный вариант решения по их мнению. Далее учащиеся переходят к этапу рассуждения, они возвращаются в первоначальные группы и каждый рассказывает свое решение, при этом остальные записывают алгоритм. Завершается "Jigsaw" общей работой, каждый алгоритм презентует один из экспертов по данному вопросу. В итоге класс выбирает, чья презентация материала была наиболее точной и эффективной, применяя способ «Бутерброд обратной связи». Использование дифференцированного задания Учитель раздает карточки с уравнениями и предлагает классу решить их Способ «Задание» А Задание 1. Вынесите общий множитель за скобки а) 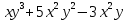б) 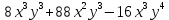В Задание 2. 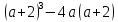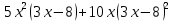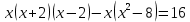Разложите на множители способом группировки а) б) С Задание 3.Решите уравнение Критерии оценивания: -знает формулы сокращенного умножения; - умеет выполнять тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения. Оценивание: самооценивание, «Сравнение с образцом». На доске выводятся верный алгоритм решения.		Карточки Приложение №2. доска Плакаты, маркеры Карточки Приложение №3. Доска
Конец урока 3 мин	6. Рефлексия. Использование стратегии «Светофор» Учащиеся на протяжении всего урока после каждого этапа оценивали себя по стратегии «Светофор». Учитель проводит рефлексию «Светофор». Каждому ученику раздает стикер, на котором они должны указать цвет получившейся и прикрепить напротив того цвета, который у них получился на конец урока. Учащиеся отмечают на листике свой получившийся цвет и по очереди, по одному выходят к доске и наклеивают свой листик напротив светофора, учитывая свои успехи на уроке. 7. 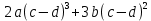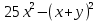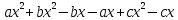Домашние задание Разложите на множители		Стикеры, плакат «Светофор». доска
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?		Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?	Охрана здоровья и соблюдение техники безопасности
В ходе урока я применила дифференциацию способами «Темп» и «Задания», чтобы учащиеся с разным по уровню усвоением учебного материала, темпераменту, могли овладеть едиными стандартами образования. Дифференцированные задания по уровню сложности, снижают уровень тревожности у учащихся, позволяют показать их возможности на базе их уровня, при этом формируя чувство собственного достоинства, этим мы решаем проблему с неуспеваемостью и повышаем мотивацию к обучению.		Методы оценивания на уроке: «Похвала», «Наводящие вопросы», «Ключ», «Сравнение с образцом», «Бутерброд обратной связи», «Светофор». Дети научатся применять теоритический материал через работу в группах, а так же научаться самооцениванию и взаимооцениванию при работе в группах, в парах и индивидуально.	Здоровьесберегающие технологии. На уроках используются упражнения для разминки и активные формы работы.
Рефлексия по уроку Была ли реальной и доступной цель урока или учебные цели? Все ли учащиеся достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке? Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?		Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце.
Итоговая оценка Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)? 1: 2: Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)? 1: 2: Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока?

Карта урока

ФИ _____________________________________ класс____________________

Приложение № 1

Тестовое задание на соответствие

Вариант 1 Вариант 2

1. (4у-3х)(3х+4у)	а. (x+2)(x2-2x+4)	1. (3х+1)³	А.16y2-9x2
2. 100m 4-4n6	б. (0.2x+1)2	2. х³+8	Б.(10m2-2n3) (10m2+2n3)
3. (3x+a)2	в.  a3-0.027	3. (а  –  5)2	В. 9x2+6ax+a2
4. х³+8	г. a2-10a+25	4. 0,04х2 + 0,4х + 1	Г.(x+2)(x2-2x+4)
5. (3х+1)³	д. 9-a2	5. (4у-3х)(3х+4у)	Д.27x3+27x2+9x +1
6. 0,04х2 + 0,4х + 1	е. (10m2-2n3) (10m2+2n3)	6. 100m 4-4n6	Е.(0.2x+1)2
7. (а-0,3)(а²+0,3а+0,09)	ж. 9x2+6ax+a2	7. (3-а)(3+а)	Ж. a3-0.027
8. (а  –  5)2	з. 16y2-9x2	8. (3x+a)2	З. a2-10a+25
9. (3-а)(3+а)	и. 27x3+27x2+9x +1	9. (а-0,3)(а²+0,3а+0,09)	И. 9-a2

Приложение № 2

Упростите выражения и найдите их значения: a) 27𝑏3 + 27𝑏2𝑎 + 12𝑏𝑎2 + 𝑎3, если 𝑎 = 2; 𝑏 = 1 d) 𝑎3 + 9 − (𝑎 + 1)(𝑎2 − 𝑎 + 1), если 𝑎 = 1	Разложите на множители: a) (𝑎 − 𝑏)(𝑎2 − 𝑐2) − (𝑎 − 𝑐)(𝑎2 − 𝑏2) b) c) (𝑥 + 𝑦)2 − 10(х2 − у2)+25(𝑥 − 𝑦)2	Докажите тождество: a)𝑎3 + 𝑏3 + 3𝑎𝑏(𝑎 + 𝑏) = (𝑎 + 𝑏)3 b) (𝑐 + 𝑑)2(с − 𝑑) + 6𝑐𝑑(𝑐 − 𝑑) + 10𝑐𝑑(𝑑 − 𝑐) = (𝑐 − 𝑑)3
Дескриптор Обучающийся - использует необходимую формулу; - выполняет преобразование выражения; - находит значение.	Дескриптор Обучающийся - выбирает необходимую формулу; - выполняет преобразование; - раскладывает многочлен на множители.	Дескриптор Обучающийся - использует ФСУ; - выполняет преобразования; - доказывает тождество.

Приложение 3

А. Задание 1. Вынесите общий множитель за скобки а) 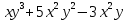б)	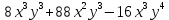Дескриптор: Обучающийся - находит общий множитель; -раскладывает многочлен на множители.
В. Задание 2. Разложите на множители способом группировки а) 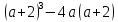б)	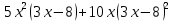Дескриптор: Обучающийся - находит общий множитель; - выполняет преобразование; - раскладывает многочлен на множители.
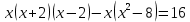
С. Задание 3.Решите уравнение	Дескриптор: Обучающийся - использует ФСУ; - выполняет преобразования; - находит неизвестное; -выполняет проверку; -записывает ответ.