вариант 1 высшая. Решение методом Гаусса x y z b
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
Задание №1 Решить систему уравнений: 1) методом Гаусса. а; 2) формулами Крамер; 3) средствами матричного исчисления 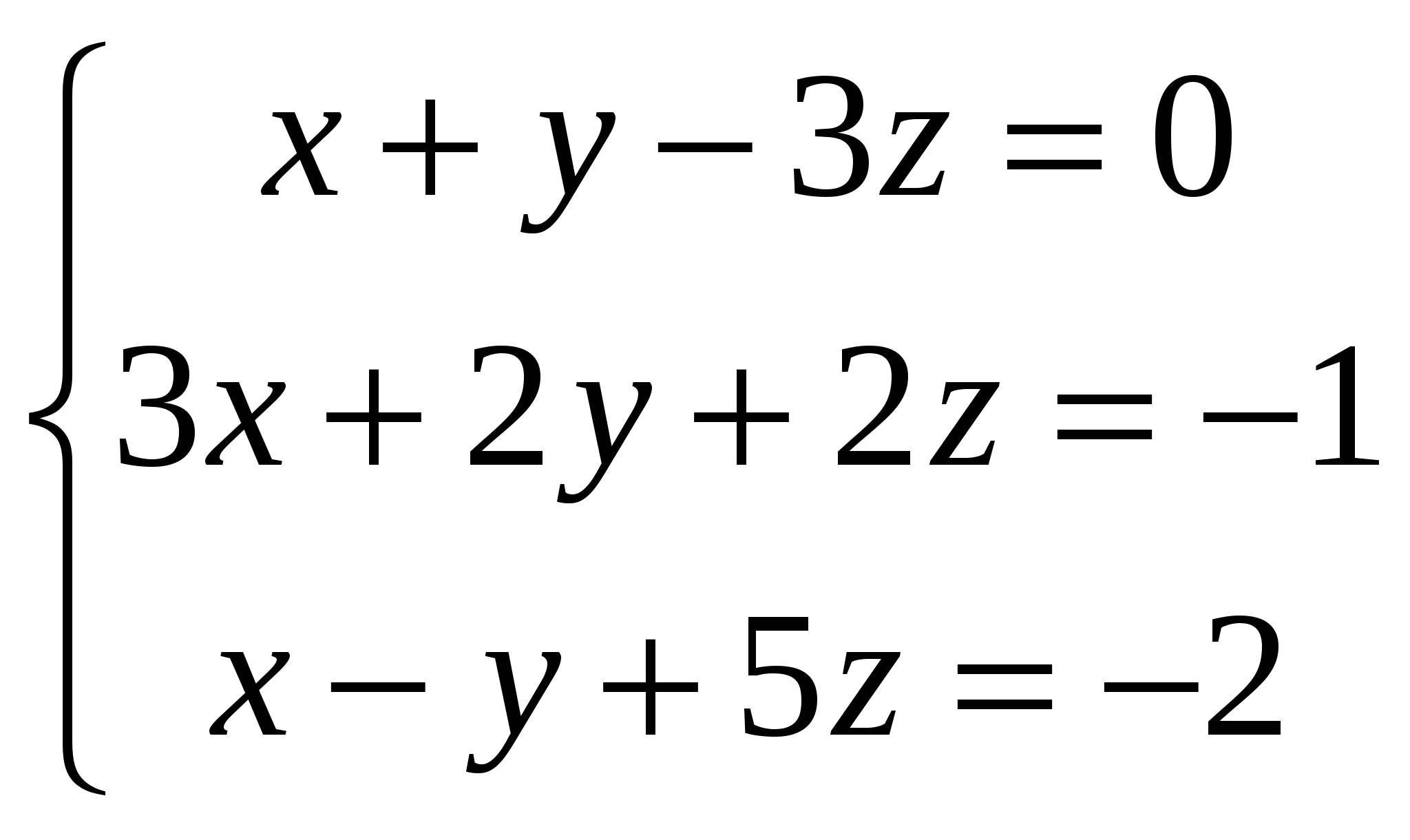 Решение:
Нашли единицу в 1-ом столбце в 1-ой строке
Умножили 1-ую строку на 3
Вычли 1-ую строку из 2-ой строки и восстановили ее
Вычли 1-ую строку из 3-ей
Нашли единицу в 2-ом столбце в 2-ой строке (изменив знак на противоположный у всей строки)
Вычли 2-ую строку из 1-ой
Умножили 2-ую строку на -2
Вычли 2-ую строку из 3-ей строки и восстановили ее
Получили единицу в 3-ем столбце разделив 3-ю строку на -14
Умножили 3-ю строку на 8
Вычли 3-ю строку из 1-ой строки и восстановили ее
Умножили 3-ю строку на -11
Вычли 3-ю строку из 2-ой строки и восстановили ее
Делаем обратный ход: Таким образом, получили z=0; Получили решение: (-1; 1; 0) пользуясь формулами Крамера Подсчитаем сначала главный определитель системы 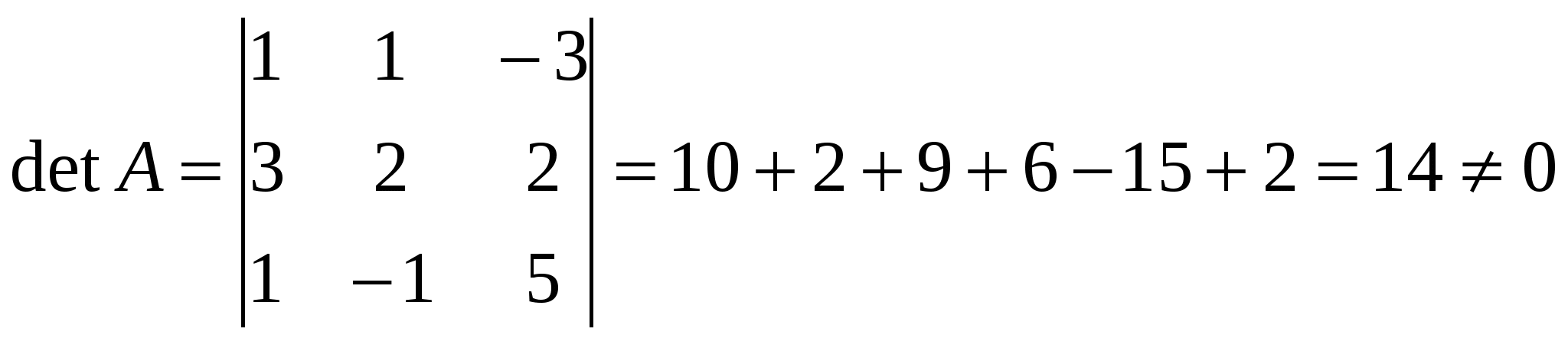 , так как детерминант не равен нулю, то делаем вывод, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители , так как детерминант не равен нулю, то делаем вывод, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители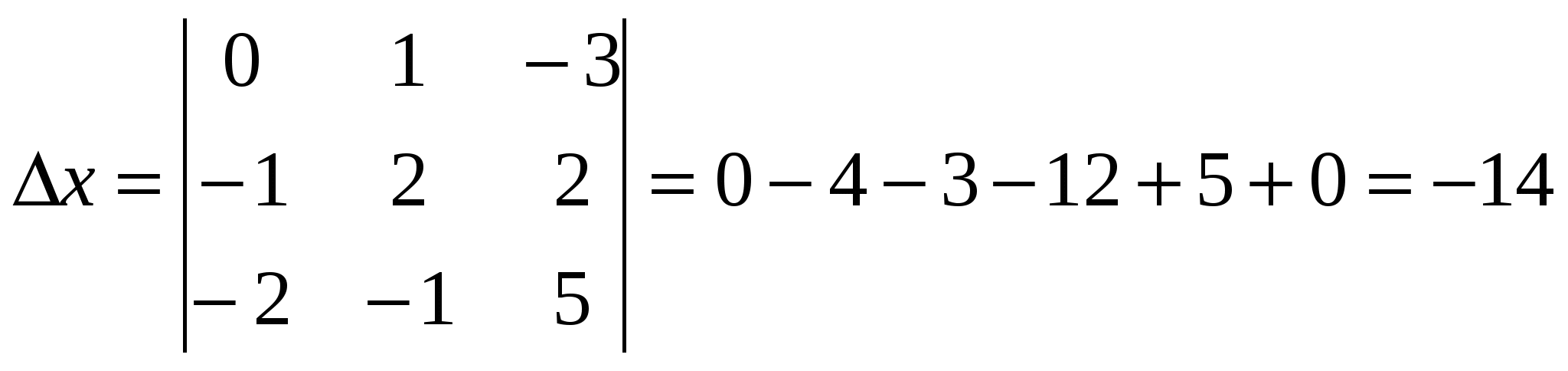 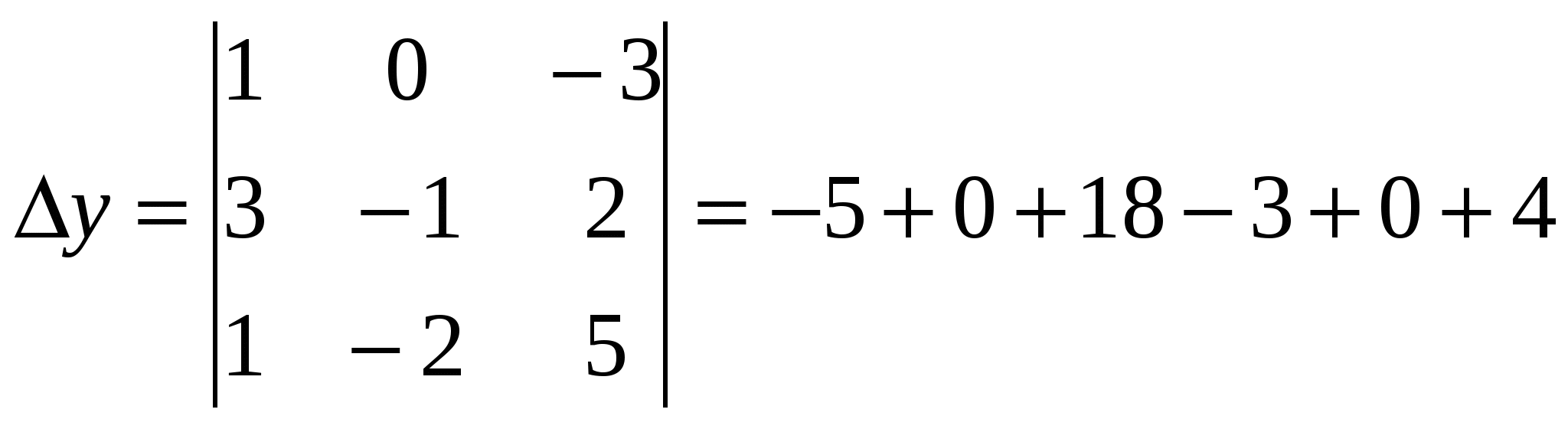 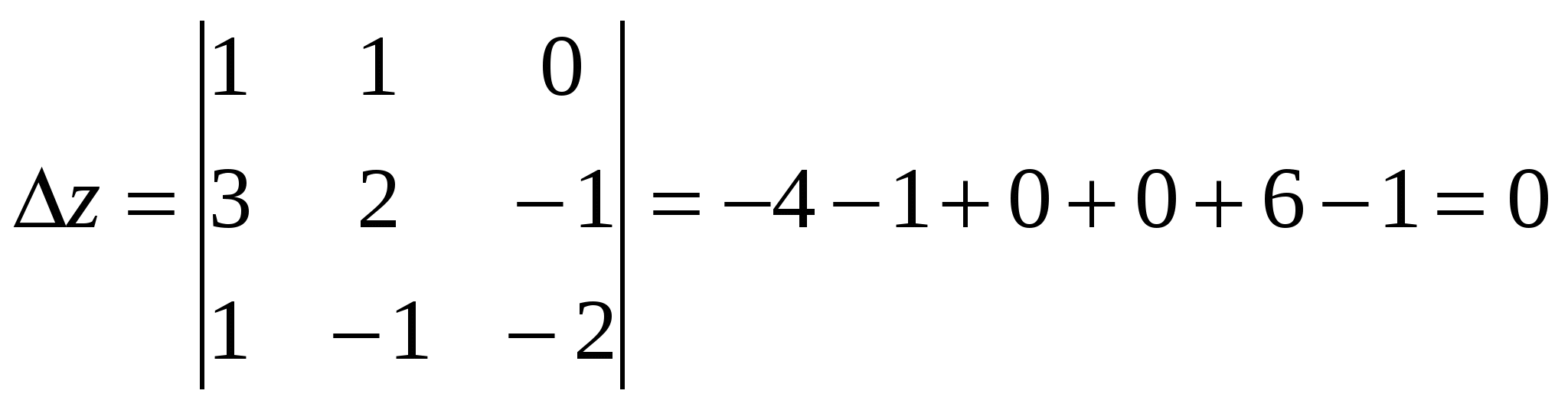 Таким образом, решение
А ∙ X = А0, Х = А-1 ∙ А0, где А-1- обратная матрица к квадратной матрице А = 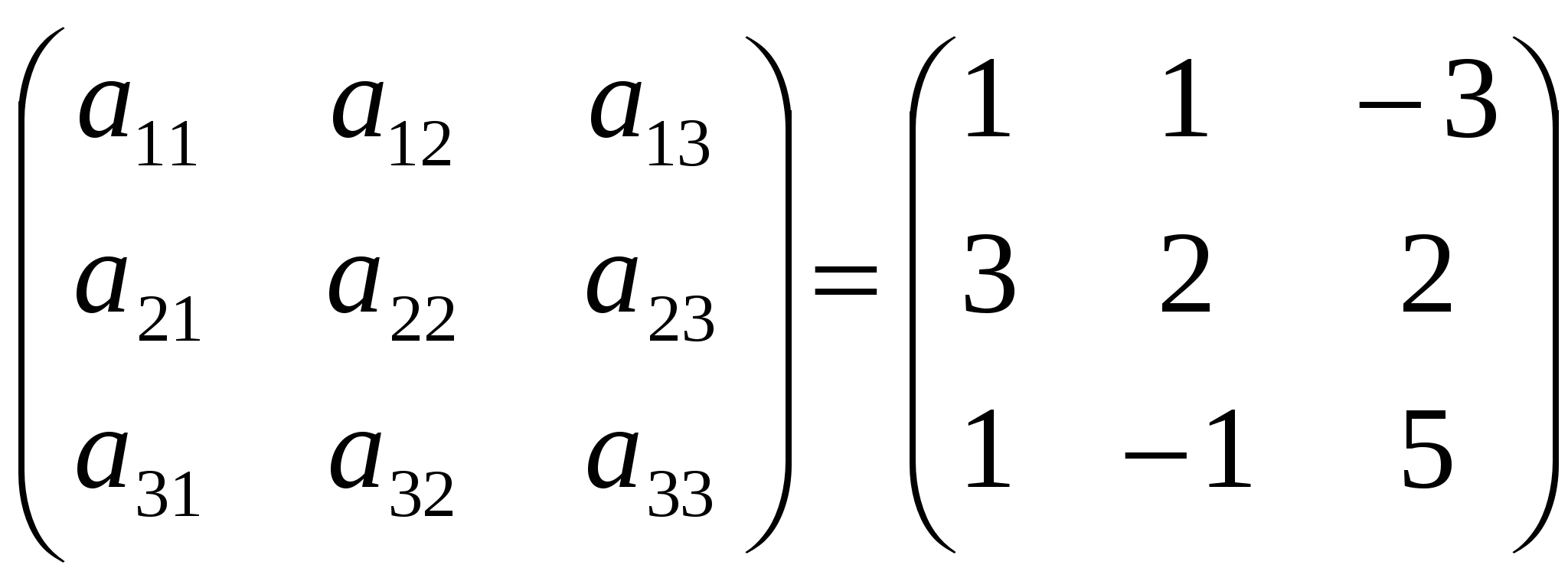 Формула для вычисления обратной матрицы А--1= 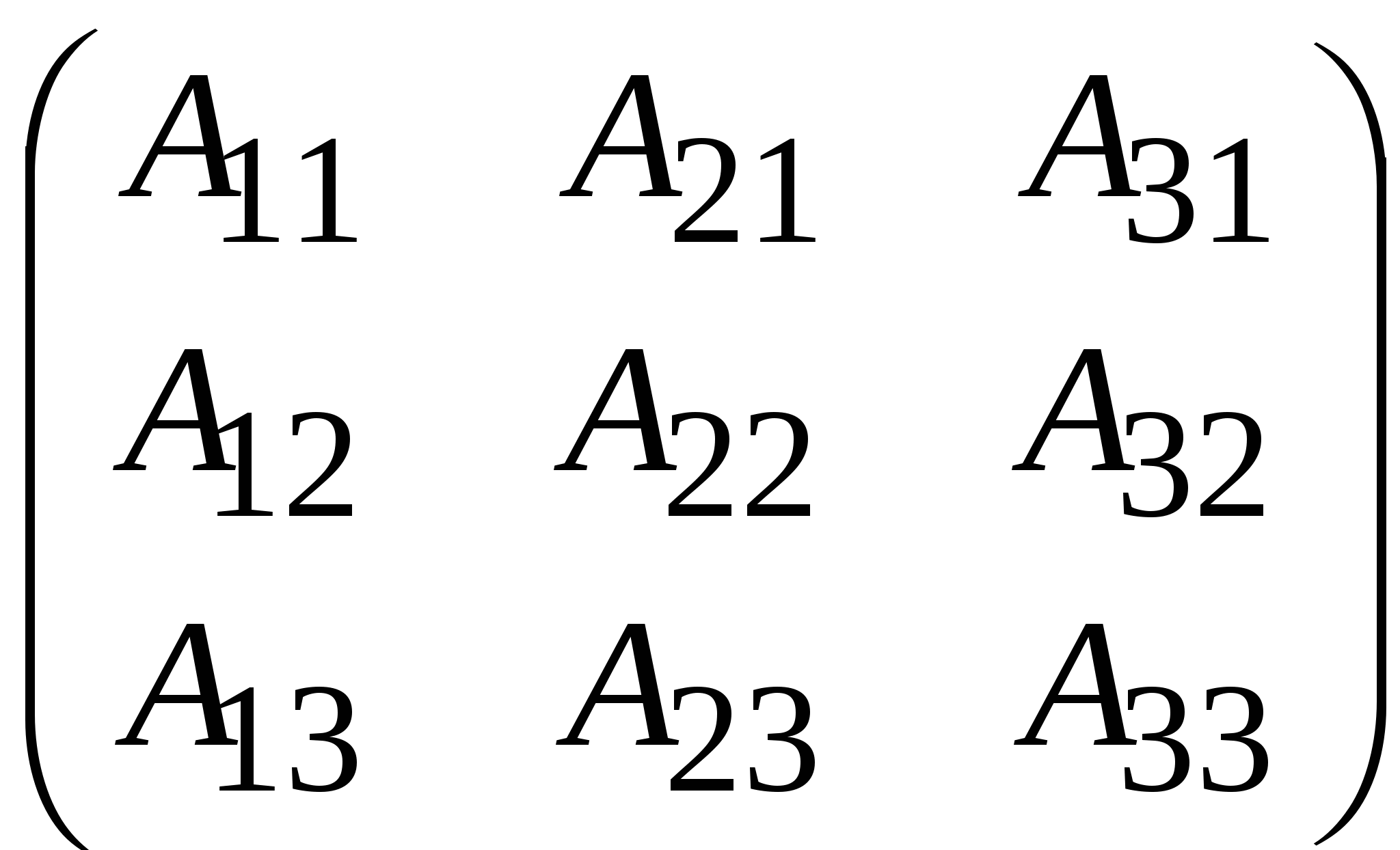 Т.к определитель матрицы А не равен 0, то матрица А невырожденная и для нее существует обратная матрица A-1. Аij называется алгебраическим дополнением к элементу Aij = (-1)1+jМ Минор
Отсюда А-1 = 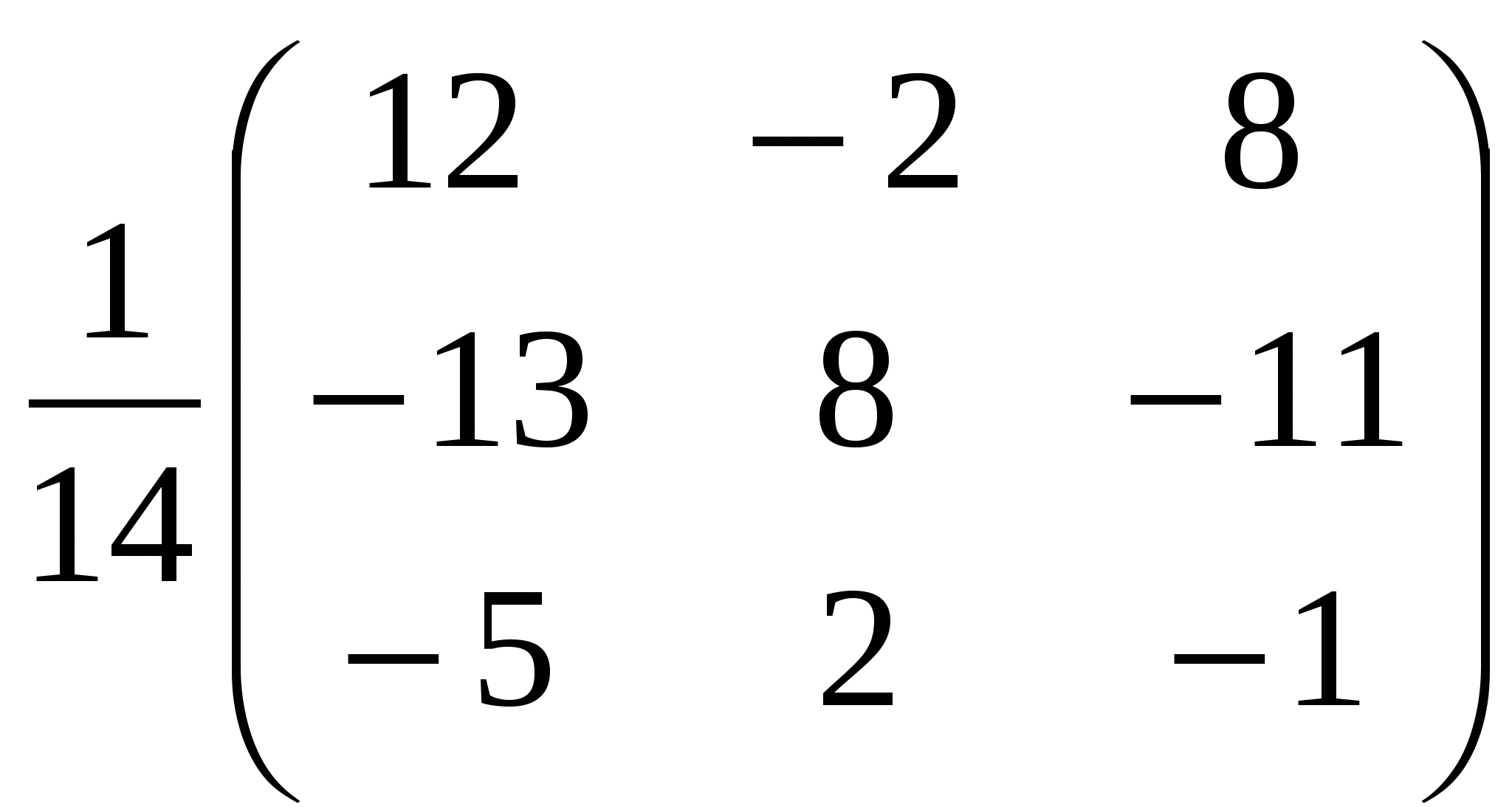 Так как Х = А-1A0 Так как Х = А-1A0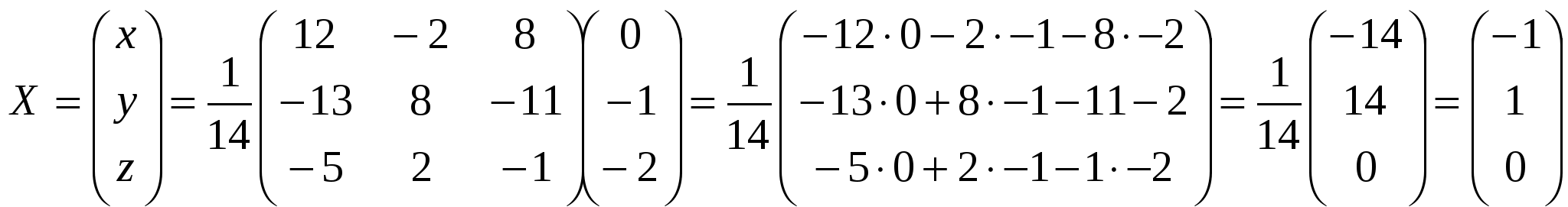 получили x=-1 у=1 z=0. Задание №2 Даны координаты треугольника АВС.
Даны координаты точек А(-8; -3), В(4; -12), C(8; 10)
расстояние в между точками А(x1; y1) и В(x2; y2) определяется по формуле
уравнение прямой проходящей через две точки А(-8; -3), В(4; -12) имеет вид уравнение прямой проходящей через две точки В(4; -12), C(8; 10) имеет вид Уравнение стороны АВ Уравнение стороны ВС
тангенс угла между двумя прямыми, угловые коэффициенты которых соответственно равны k1 k2, вычисляются по формуле 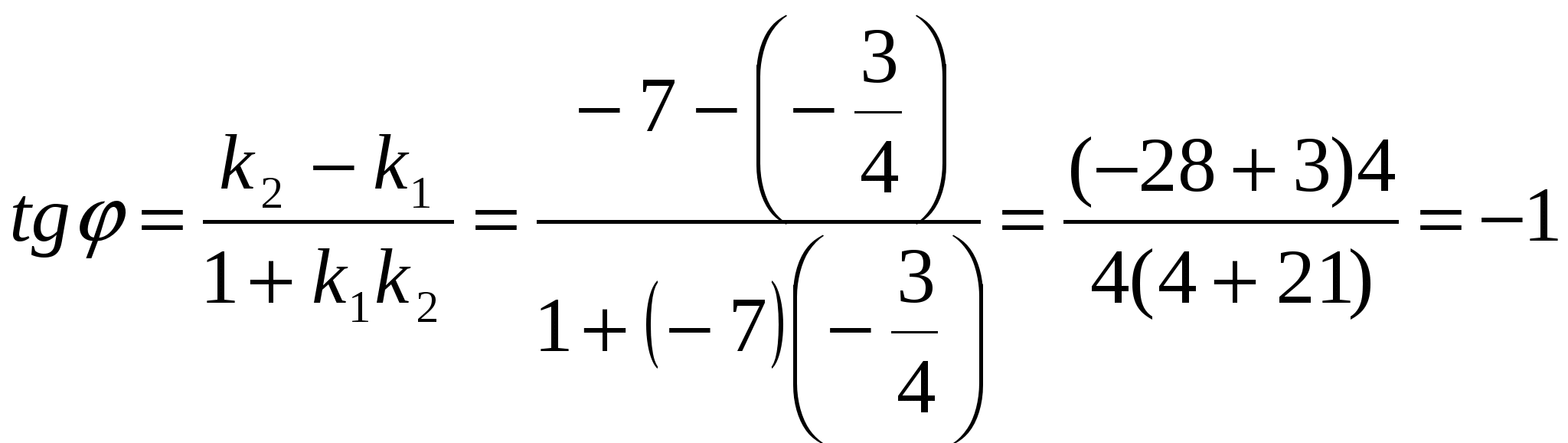 из этого найдем угол из этого найдем угол
угловые коэффициенты перпендикулярных прямых с угловыми коэффициентами k1 k2 связаны соотношением 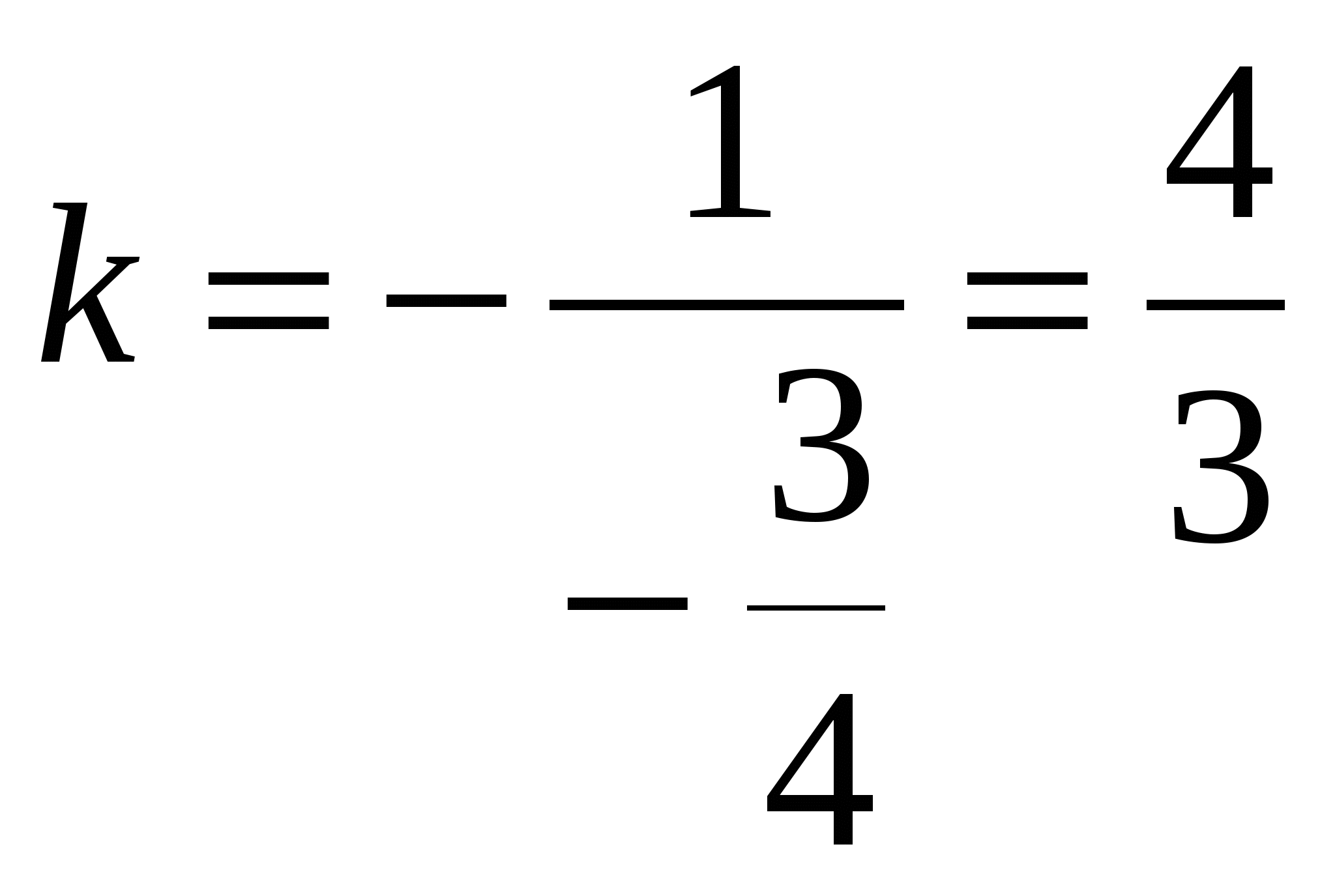 , теперь находим уравнение: уравнение прямой проходящей через данную точку в заданном направлении. Имеет вид , теперь находим уравнение: уравнение прямой проходящей через данную точку в заданном направлении. Имеет вид для нахождение длины высоты CD найдем координаты точки D 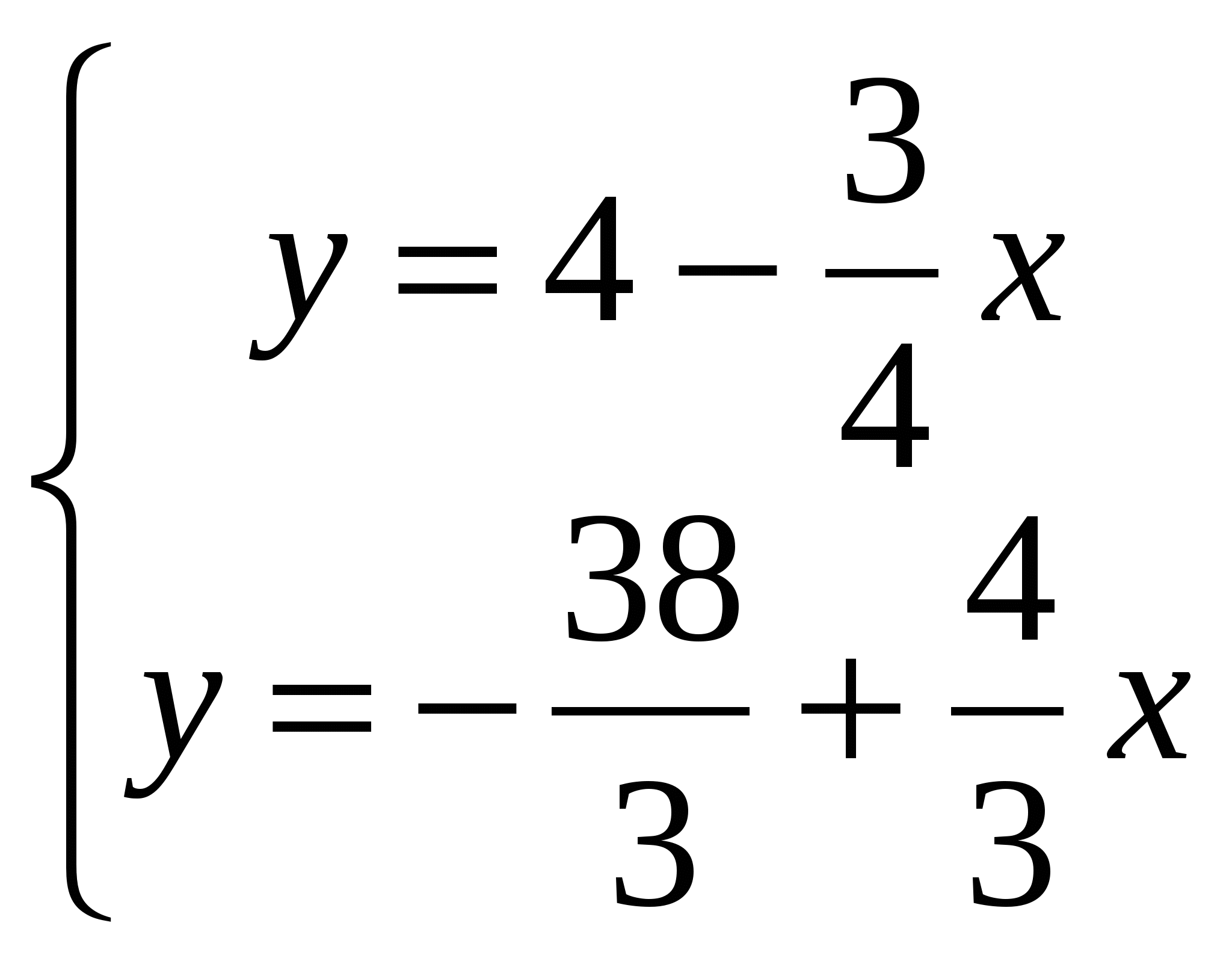 решая данную систему находим координаты точки D (8; -2) решая данную систему находим координаты точки D (8; -2)длина высоты:
координаты середины отрезка В(16;-8), C(14;6) имеем координаты точки Е(15;-1), найдем уравнение медианы АЕ уравнение прямой проходящей через две точки А(4;1), Е(15;-1) имеет вид угловой коэффициент координаты точки К пересечения этой медианы с высотой CD 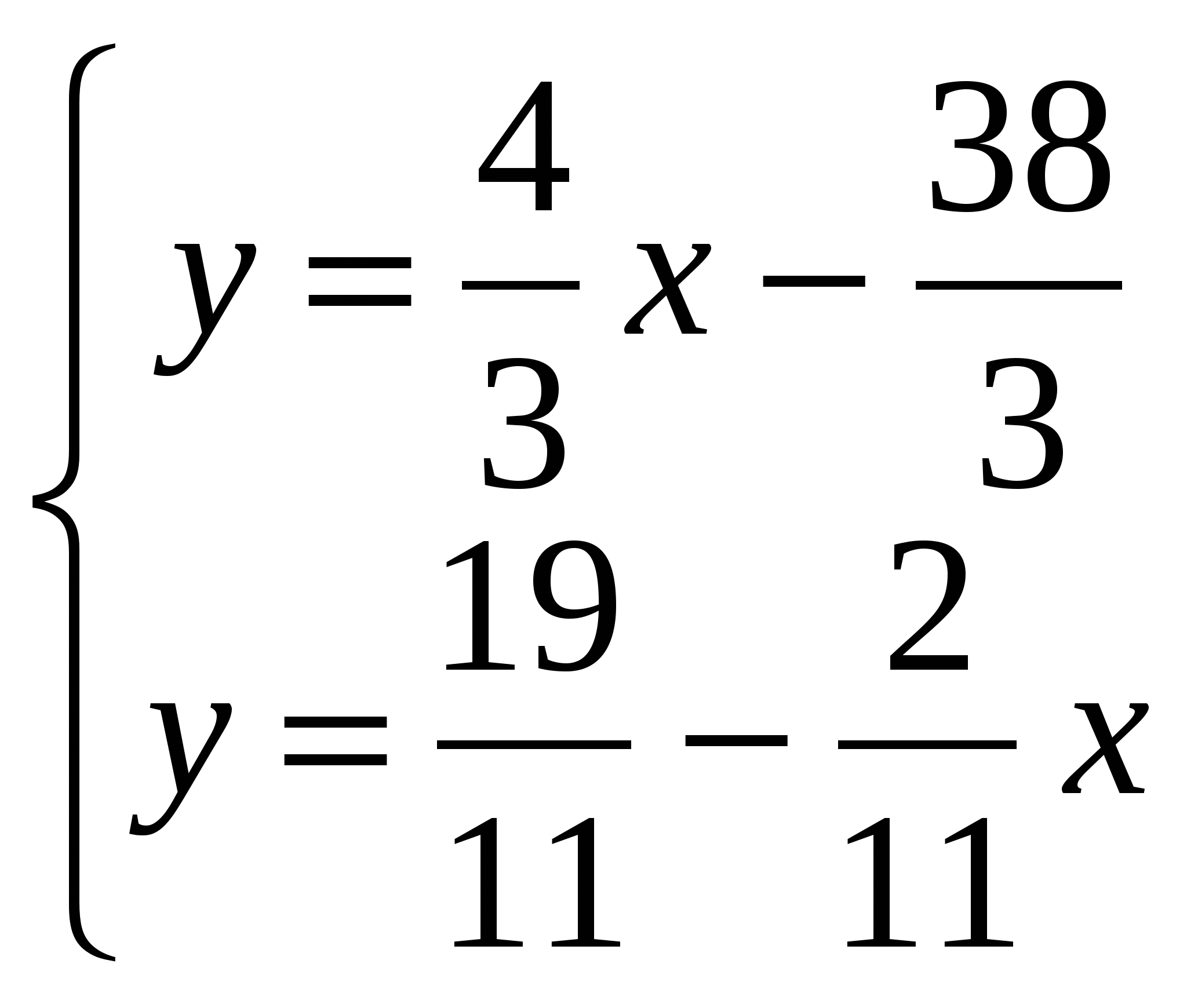 решая данную систему находим координаты точки К (9,5; 0) решая данную систему находим координаты точки К (9,5; 0)
У параллельных прямых угловые коэффициенты совпадают Угловой коэффициент прямой построенной на стороне АВ равен Координаты точки К (9,5; 0) уравнение прямой проходящей через данную точку в заданном направлении. Имеет вид
координаты точек А(4;1) D (8; -2) координаты середины отрезка AM где середина отрезка является точка D, выразим из этих уравнений координаты точки М Задание №3 Установить, какие линии определяются следующими уравнениями, изобразить их на чертеже. а) преобразуем данное уравнение следующим образом уравнение параболы Изображаем чертеж 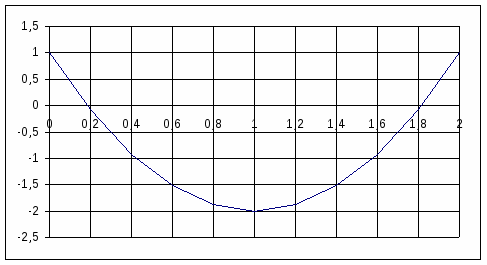 б) возведем обе части уравнения в квадрат Так как по условию 0x, то уравнение Изобразим чертеж 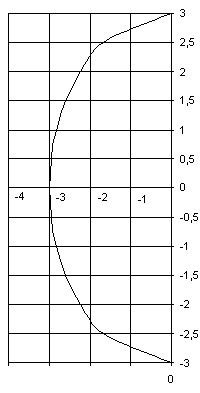 Задание № 4 Исследовать функцию и построить график
вертикальные асимптоты горизонтальные асимптоты наклонные асимптоты 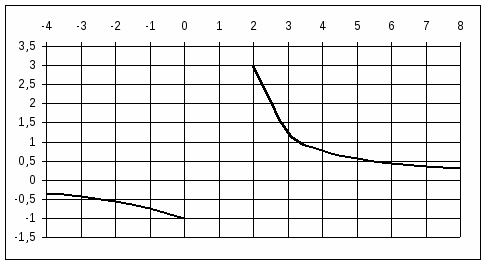
- точек перегиба нет
точка пересечения с осью OY Задание № 5 Найти неопределенные интегралы (результата а), б)) проверить дифференцированием) а) Проверка б) проверка Задание № 6 Решить дифференциальные уравнения а) y(1)=1 б) Задание № 7 Сколько существует способов составления в случайном порядке списка из 7 кандидатов для выбора на руководящую должность? Какова вероятность того, что кандидаты будут расставлены в списке по возрасту (от меньшего к большему)? Решение: Так как порядок кандидатов по условию значения не имеет, то имеем задачу о числе перестановок семи разных кандидатов. Следовательно, Благоприятствующее событие, что кандидаты будут расставлены по возрасту только одно, следовательно вероятность будет равна Задание № 8 В районе 24 чел. обучается на заочном факультете института, из них 6 на факультете механизации, 12 на – агрономическом факультете и 6 – на экономическом. Вероятность успешно сдать все экзамены на предстоящей сессии для студентов факультета механизации равна 0,6. агрономического – 0,76 и экономического факультета – 0,8. А) найти вероятность того, что наудачу взятый студент, сдавший успешно все экзамены, окажется студентом экономического факультета Б) студент сдал все экзамен. Какова вероятность того, что он учится на агрономическом факультете Решение Событие А – наудачу взятый студент факультета механизации Событие В – наудачу взятый студент агрономического факультета Событие С – наудачу взятый студент экономического факультета 1. Вероятность того, что студент факультета механизации сдаст все экзамены успешно - равна 0,6 2. Вероятность того, что студент агрономического факультета сдаст все экзамены успешно - равна 0,76. 3. Вероятность того, что студент экономического факультета сдаст все экзамены успешно - равна 0,8. вероятность того, что выбранный студент – студент факультета механизации 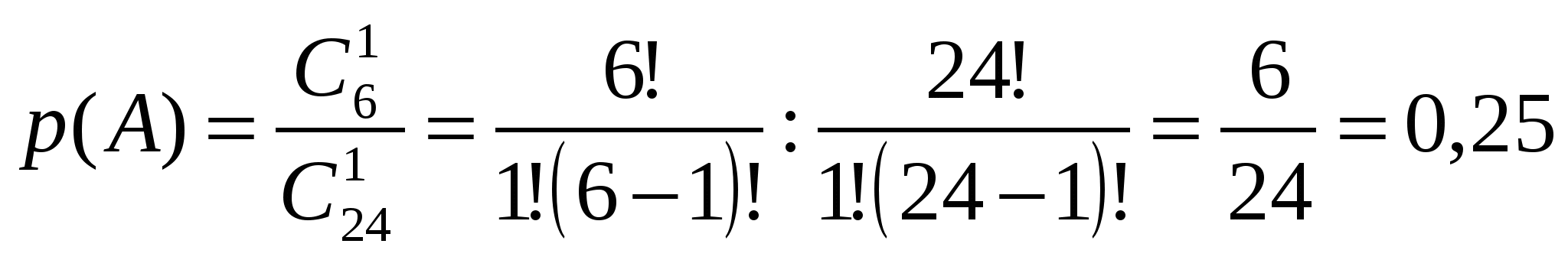 вероятность того, что выбранный студент – студент агрономического факультета 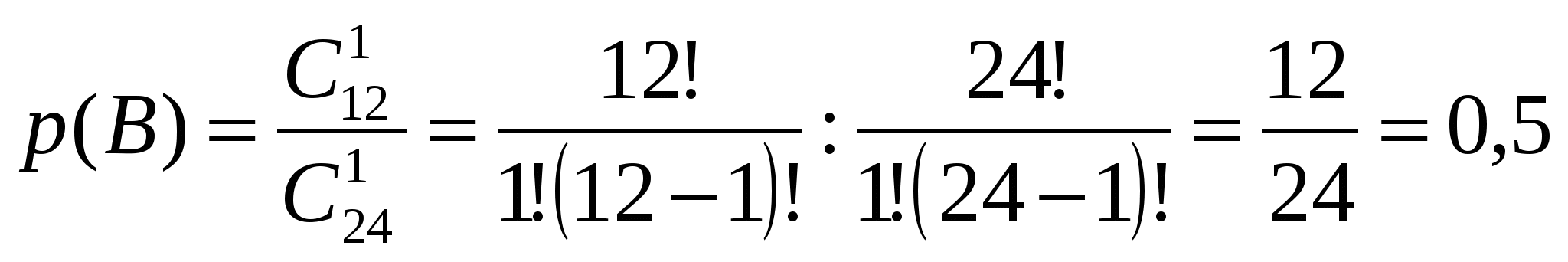 вероятность того, что выбранный студент – студент экономического факультета 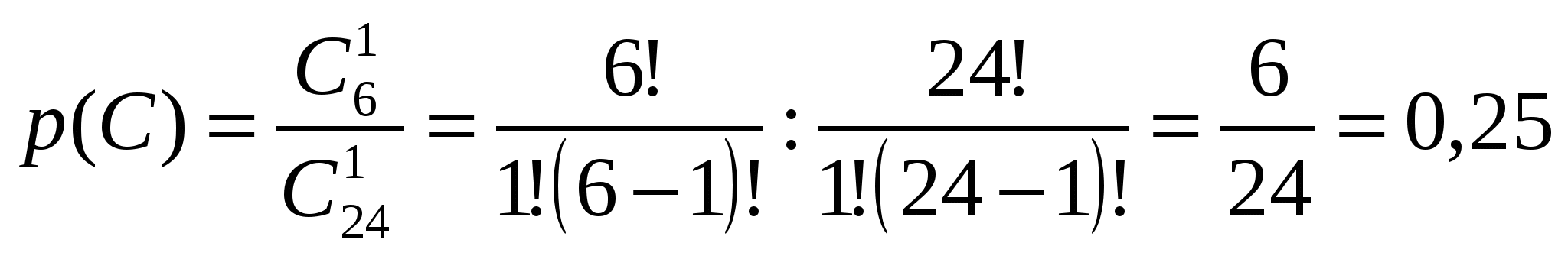 Вероятность того, что случайно выбранный студент сдал все экзамены будет равна вероятность того, что наудачу взятый студент, успешно сдавший экзамены, является студентом экономического факультета - рассчитываем по формуле Бейеса 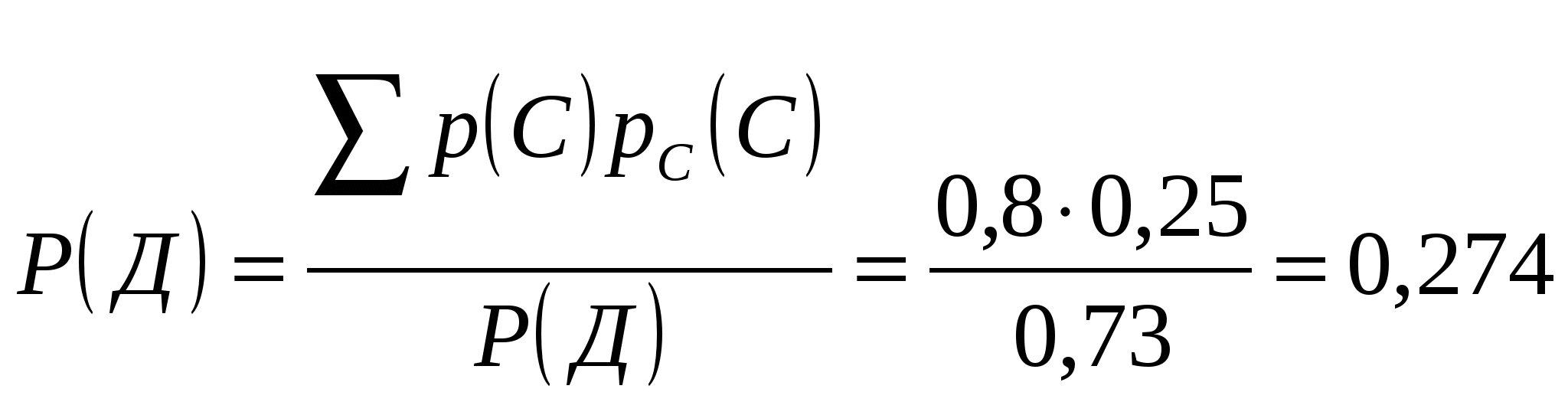 вероятность того, что наудачу взятый студент, успешно сдавший экзамены, является студентом агрономического факультета - рассчитываем по формуле Бейеса 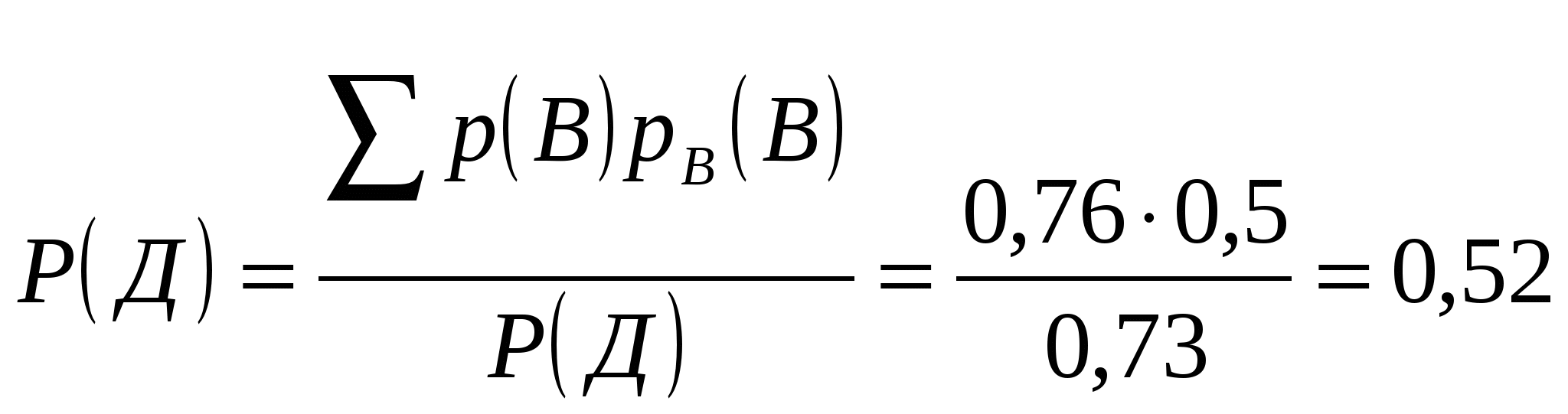 Задание № 9 Задана 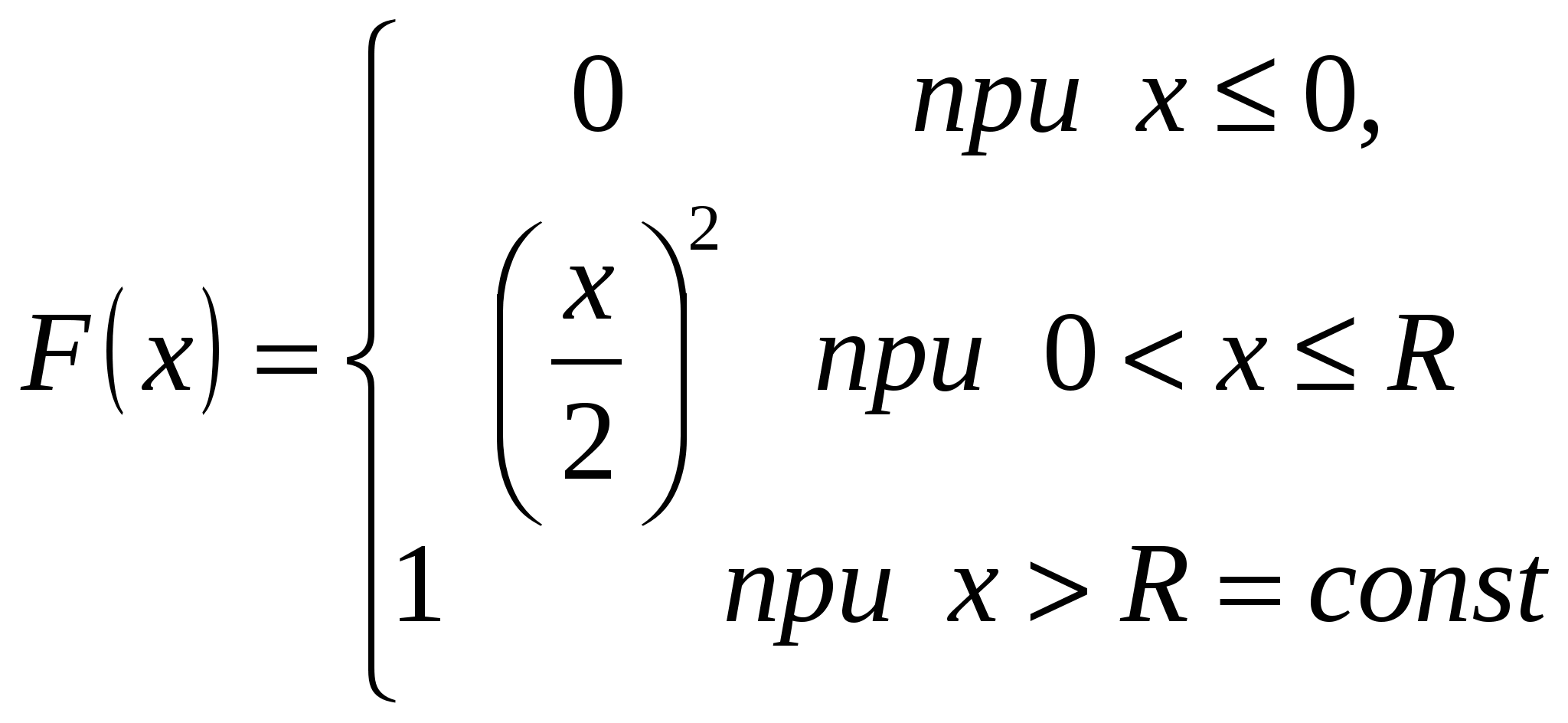 - функция распределения случайной величины Х. - функция распределения случайной величины Х.Найти а) f(x), б) М(Х), D(X), (x). в) построить графики F(x) и f(x) Найдем f(x) 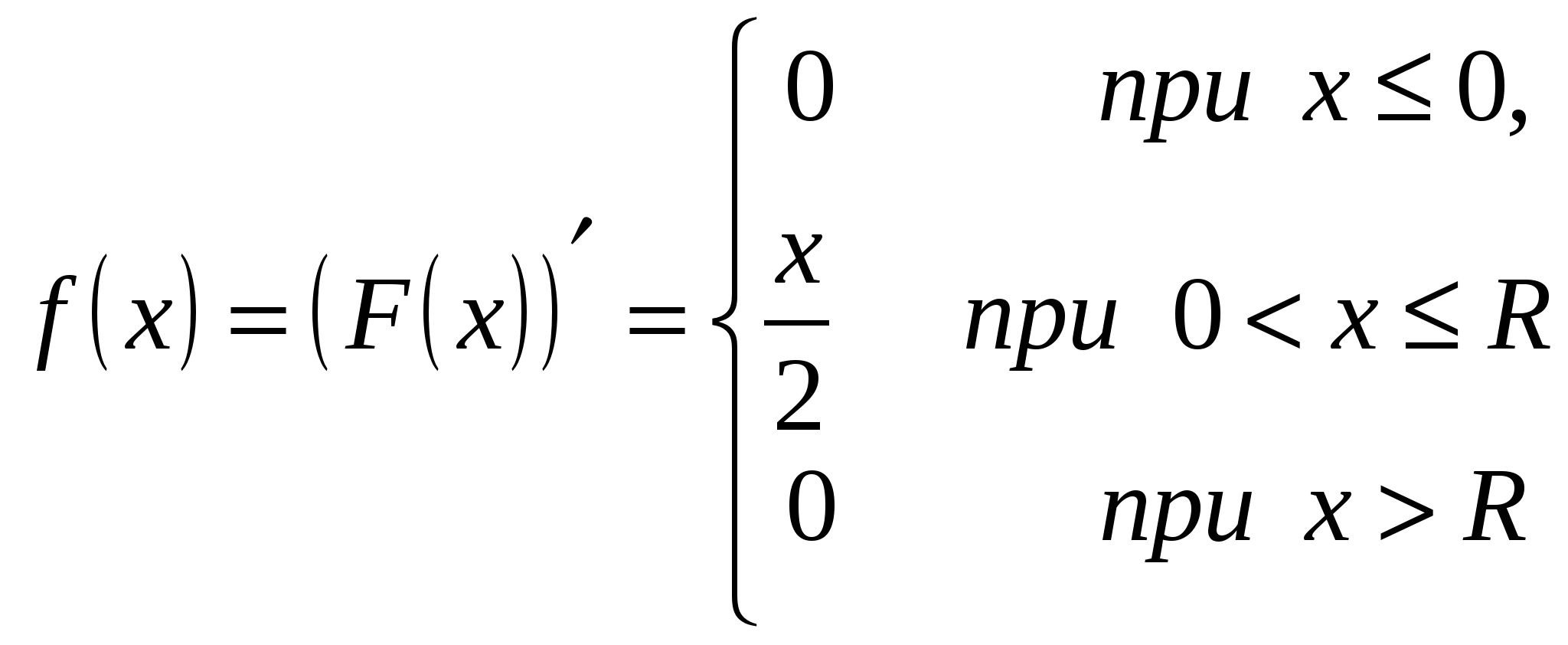 найдем математическое ожидание построим графики F(x) и f(x) 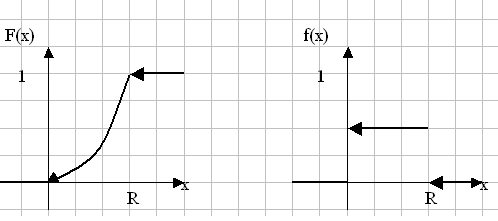 Задание № 10 По данным выборочного обследования получены следующие распределения семей по среднедушевому доходу
Построить гистограмму распределения частот. Найти среднедушевой доход семьи в выборке, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объяснить полученные результаты. Данные о б обследовании представлены в виде интервального вариационного ряда – с неравными интервалами: интервалы разности (разность между верхней и нижней границами) интервалов неодинаковы. Условно закроем границы интервалов. Интервальная разность второго интервала 50-25= 25 следовательно нижняя граница первого интервала 25-25=0 интервальная разность предпоследнего интервала 150-125=25 следовательно верхняя граница последнего интервала 150+25=1750 в результате. Получим следующий вариационный ряд
Рассчитаем абсолютную плотность распределения
Построим гистограмму 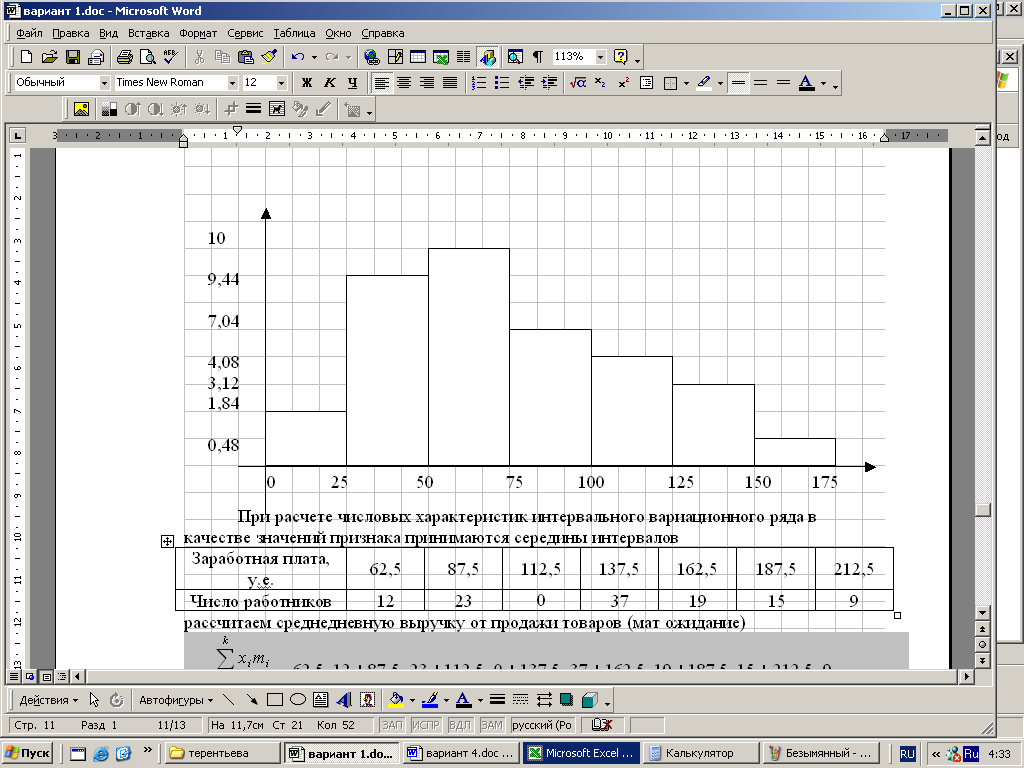 При расчете числовых характеристик интервального вариационного ряда в качестве значений признака принимаются середины интервалов
рассчитаем среднедневную выручку от продажи товаров (мат ожидание) 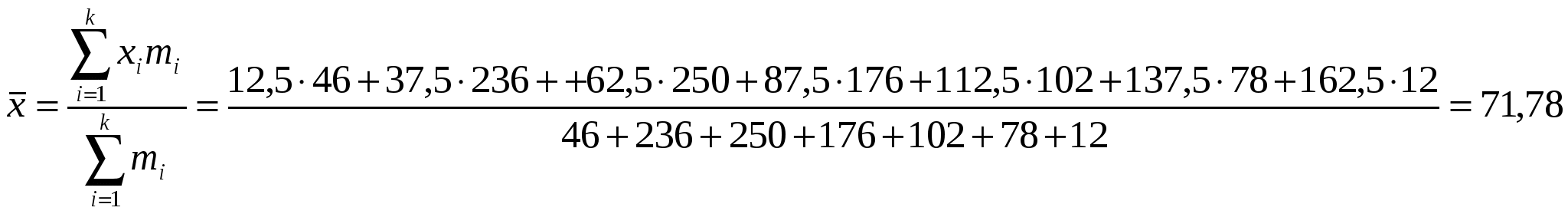 дисперсия 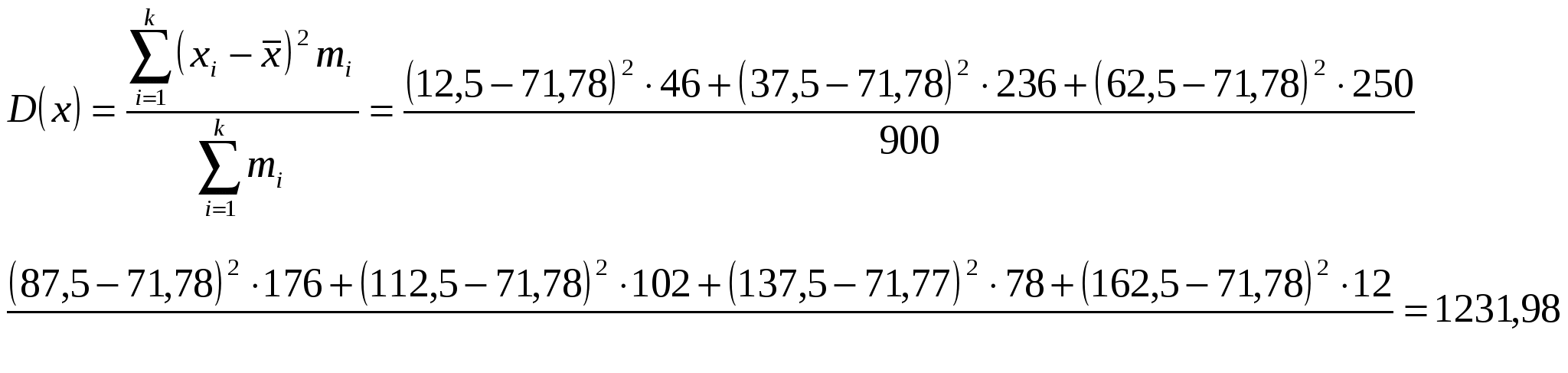 среднее квадратическое отклонение найдем коэффициент вариации коэффициент вариации составляет 48,889 %. Поскольку он больше 35 % можно сделать вывод о том, что изучаемая совокупность заработной платы является не однородной, что обусловило высокую коллеблемость среднедушевого дохода семьи. Следовательно, использование средней арифметической для характеристики наиболее типичного уровня среднедушевого дохода семьи не Задание № 11 Врач исследователь выявляет звависимость площади пораженной части легких у людей, заболевших эмфиземой легких, от числа лет курения. Статистические данные, собранные им в некоторой области, имеют следующий вид: Х – число лет курения. Y – площадь пораженной части легких %.
Построить график исходных данных и определите по нему характер зависимости. Рассчитать выборочный коэффициент линейной корреляции Пирсона, проверить его значимость при а=0,05. построить уравнение регрессии и дать интерпретацию полученных результатов. Если человек курит 30 лет, то сделать прогноз о степени поражения легких у случайно выбранного пациента, больного эмфиземой. Данные, приведенные в таблице, представим в виде точечной диаграммы 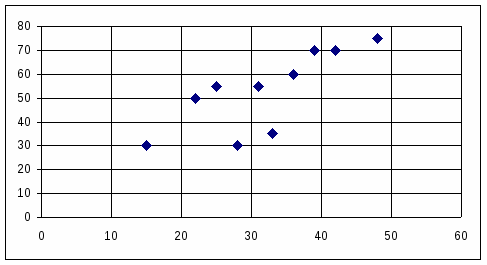 Диаграмма наглядно показывает наличие линейной зависимости площади поражения части легких от числа лет курения. С увеличением лет курения увеличивается площадь поражения. Рассчитаем выборочный коэффициент линейной корреляции Пирсона проверим его значимость при а = 0,05.
Найдем средние значения 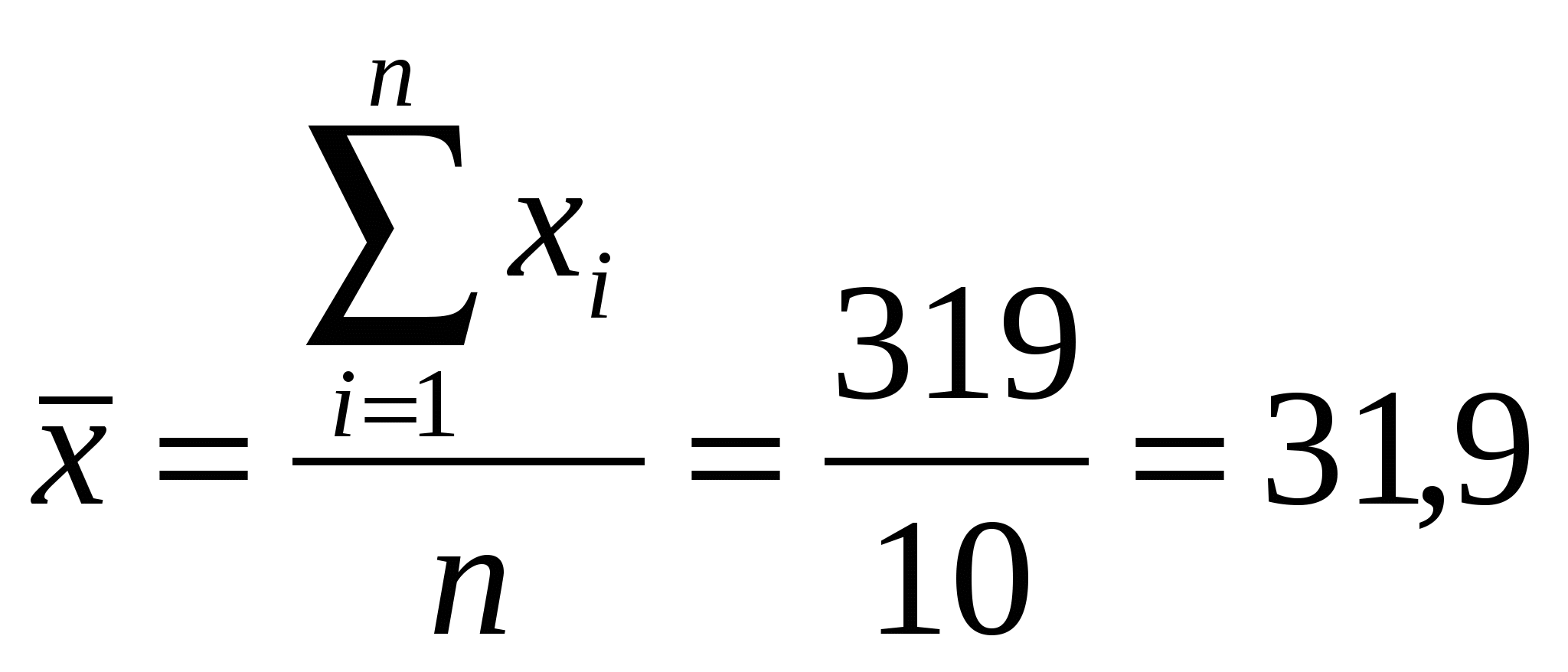 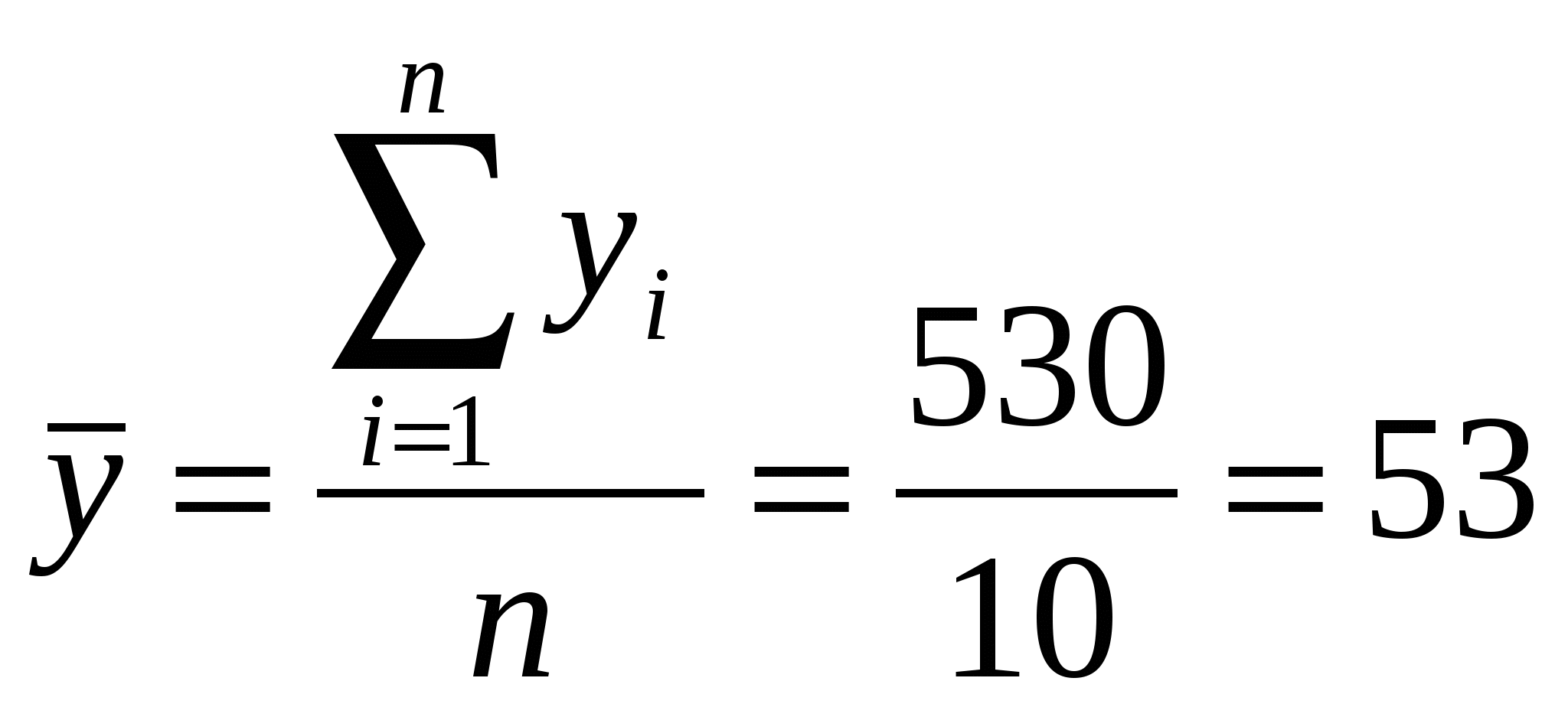 Для нахождения коэффициента корреляции воспользуемся формулой 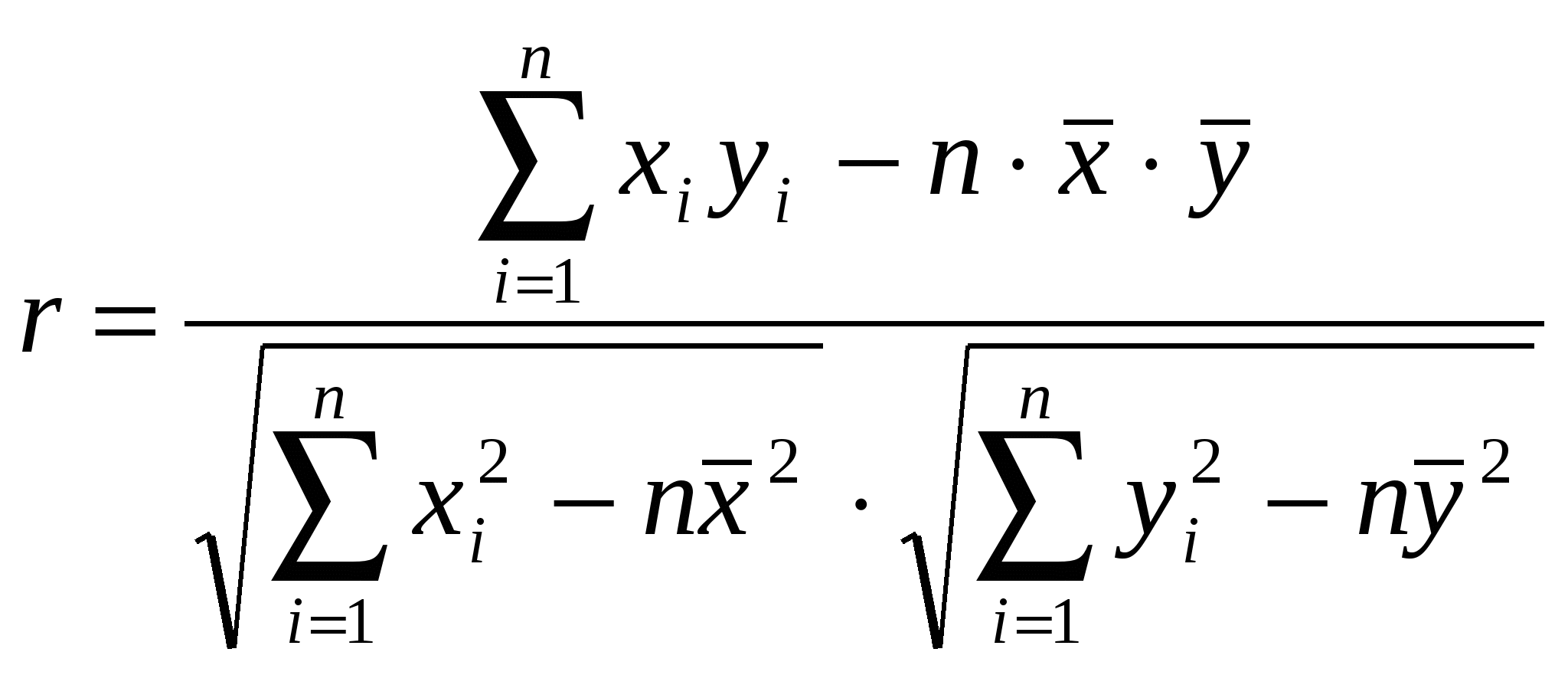 Проверим значимость коэффициента r=-0,937 при а=0,01. для этого найдем 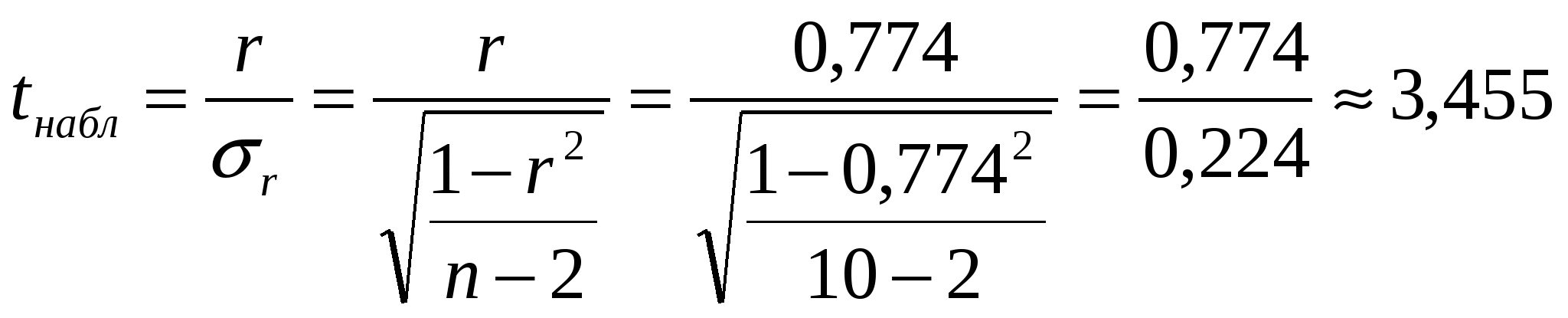 и и 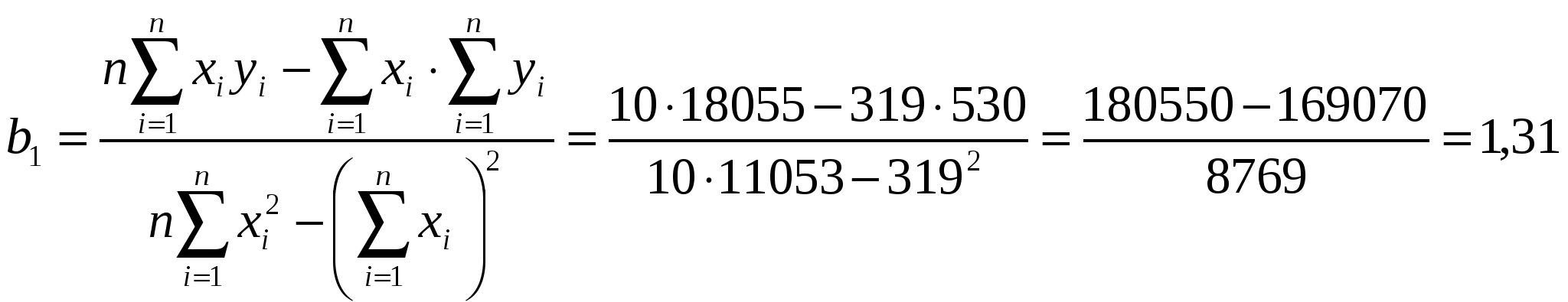 следовательно, уравнение регрессии имеет вид коэффициент b1 – характеризует наклон линии регрессии b1=1,31. это означает, что при увеличении х на единицу ожидаемое значение y увеличится на 1,31. то есть регрессионная модель указывает на то, что каждое увеличение лет курения увеличивает область поражения легких на 1,31. отсюда b1 может быть интерпретирован как изменение площади пораженной части легких, который варьирует в зависимости от числа лет курения. Свободный член уравнения b0 =11,211 это – значение y при х. Можно интерпретировать b0 как меру влияния на площадь поражения легких другими факторами, не включенных в уравнение регрессии. |
