Задача 1. Решение Начальный объем газа находим из уравнения состояния (1) где газовая постоянная углекислого газа (справочные данные)
 Скачать 183 Kb. Скачать 183 Kb.
|
|
Задача 1 Считая теплоемкость идеального газа зависящей от температуры, определить: параметры газа в начальном и конечном состояниях, изменение внутренней энергии, теплоту, участвующую в процессе и работу расширения. Исходные данные, необходимые для решения задачи, выбрать из табл. 1., зависимость величины теплоемкости от температуры приведена в приложении 1. Таблица 1
Решение Начальный объем газа находим из уравнения состояния: где из формулы (1) По приложению 1 определяем средние молярные изобарные теплоемкости углекислого газа: - при - при Средняя молярная теплоемкость при постоянном давлении; Средняя массовая теплоемкость при постоянном давлении; где Массовую изохорную теплоемкость смеси находим из уравнения Майера: Показатель адиабаты: Конечный давление и объем газа находим из соотношения параметров в адиабатном процессе: 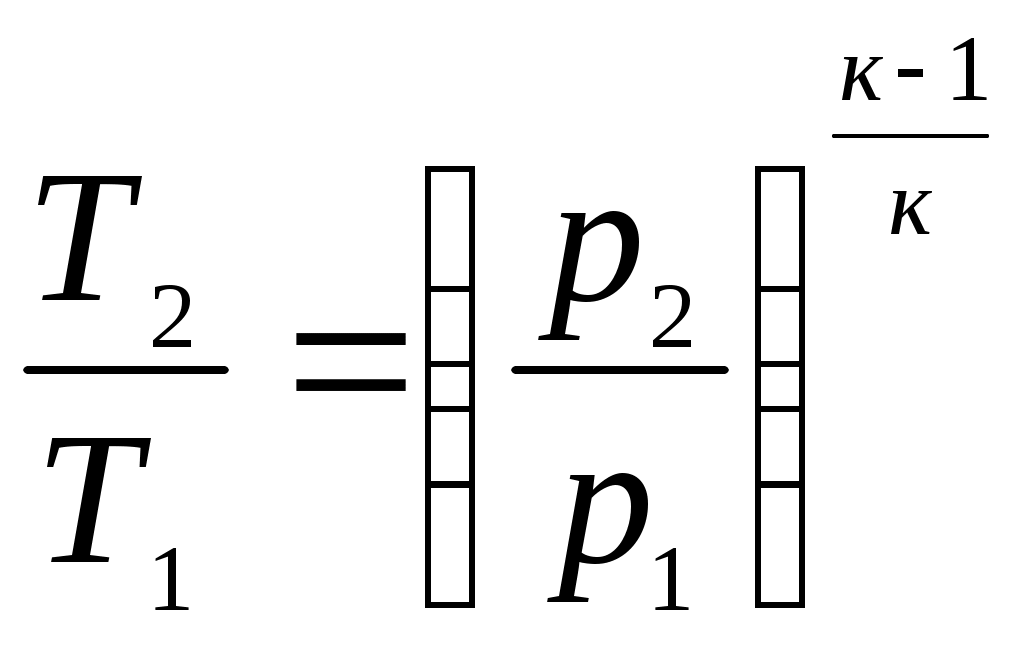 (7) (7)откуда 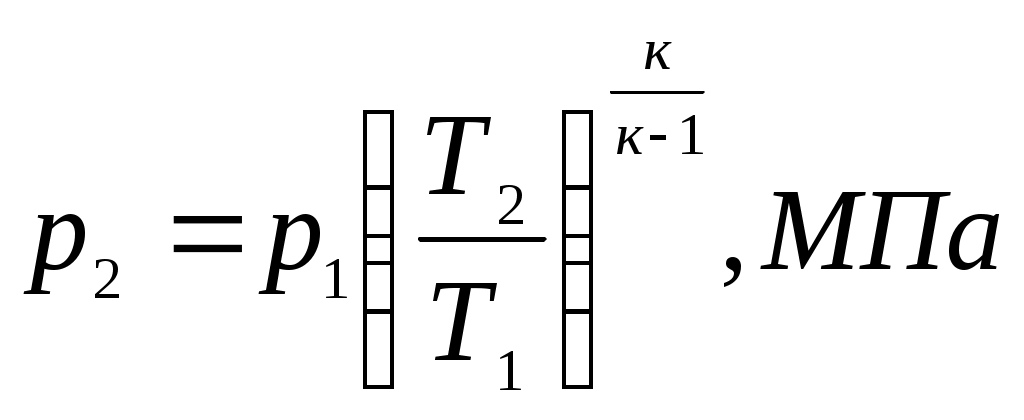 (8) (8)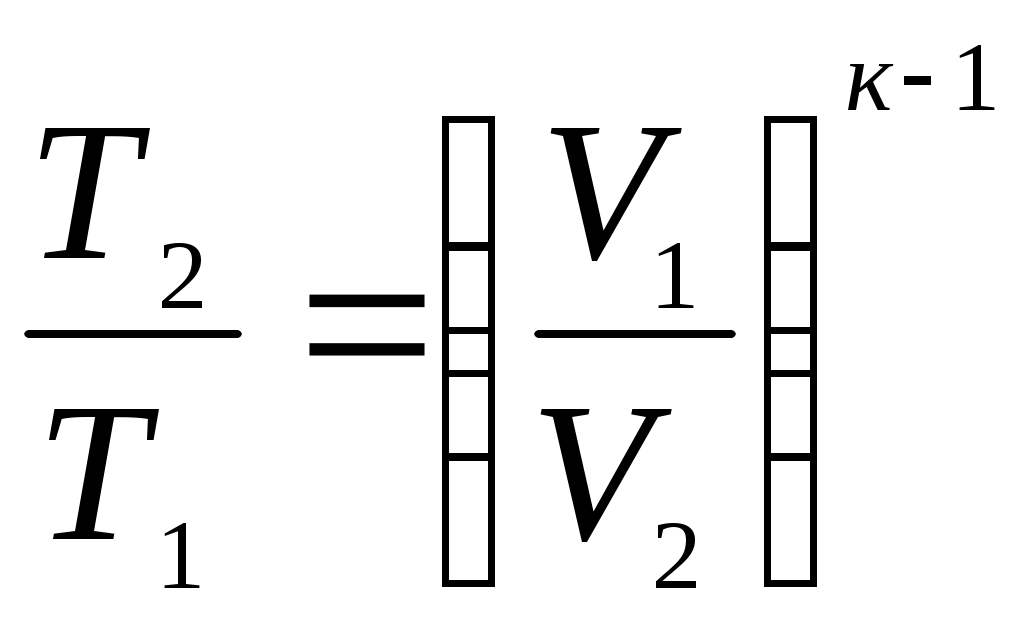 (9) (9)откуда 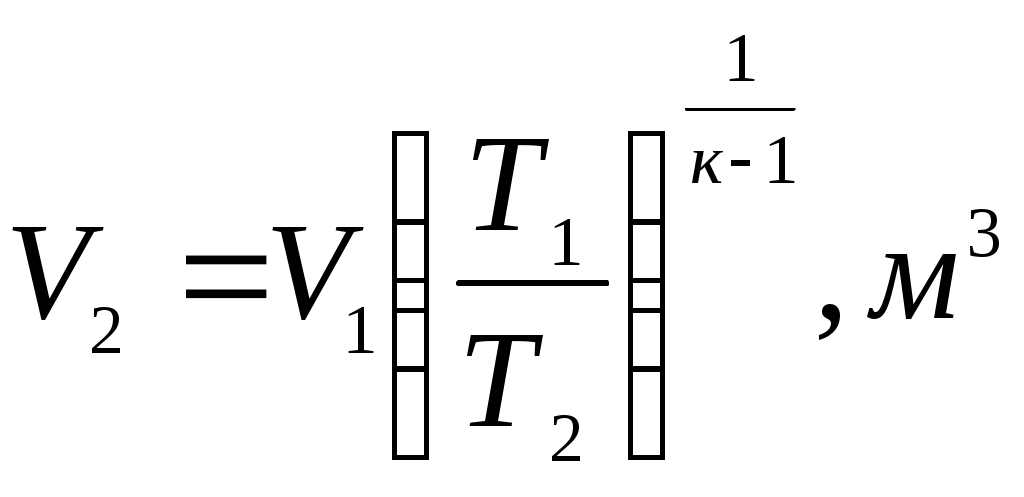 (10) (10)Теплота, участвующая в процессе: Работа расширения: Изменение внутренней энергии: 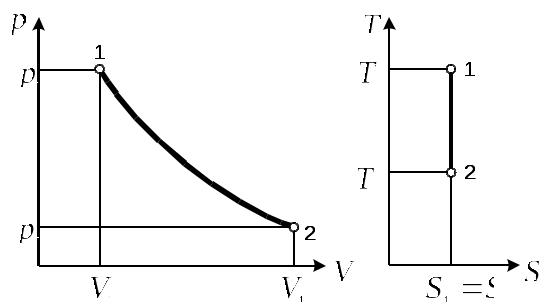 Рисунок 1 - Адиабатный процесс в Вывод: В адиабатном процессе теплота не подводится и не отводится |
