математика практические задания. Практическое задание. Решение Находим уравнение изоклин f ( x, y ) k, где k const, следовательно k
 Скачать 328.14 Kb. Скачать 328.14 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА Группа Чи19М491 Студент Александр Вениаминович Чипизубов МОСКВА 2020 1. Методом изоклин построить интегральные кривые уравнения 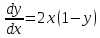 Решение: 1. Находим уравнение изоклин. f(x,y)=k, гдеk=const, следовательноk=2x(1-y)⇒ 1-y=k/2x⇒y=1-k/2x 2. Рассчитываем углы наклона изоклин при различных значенияхk. Приk=0 y=1, tgα=0⇒ α=0 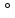 При k=1 y=1-1/2x, tgα=1⇒ α=45  При k=-1 y=1+1/2x, tgα=-1⇒ α=135  При k=2 y=1-1/2x, tgα=2⇒ α=63 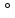 При k=-2 y=1+1/2x, tgα=-2⇒ α=117 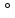 Приk=3 y=1-1/2x, tgα=3⇒α=72 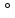 Приk=-3 y=1+1/2x, tgα=-3⇒α=288 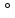 и т.д. и т.д.3.В каждой точке с координатами (x,y) строим отрезок с угловым наклоном k=f(x), затем проводим касательные к этим отрезкам. 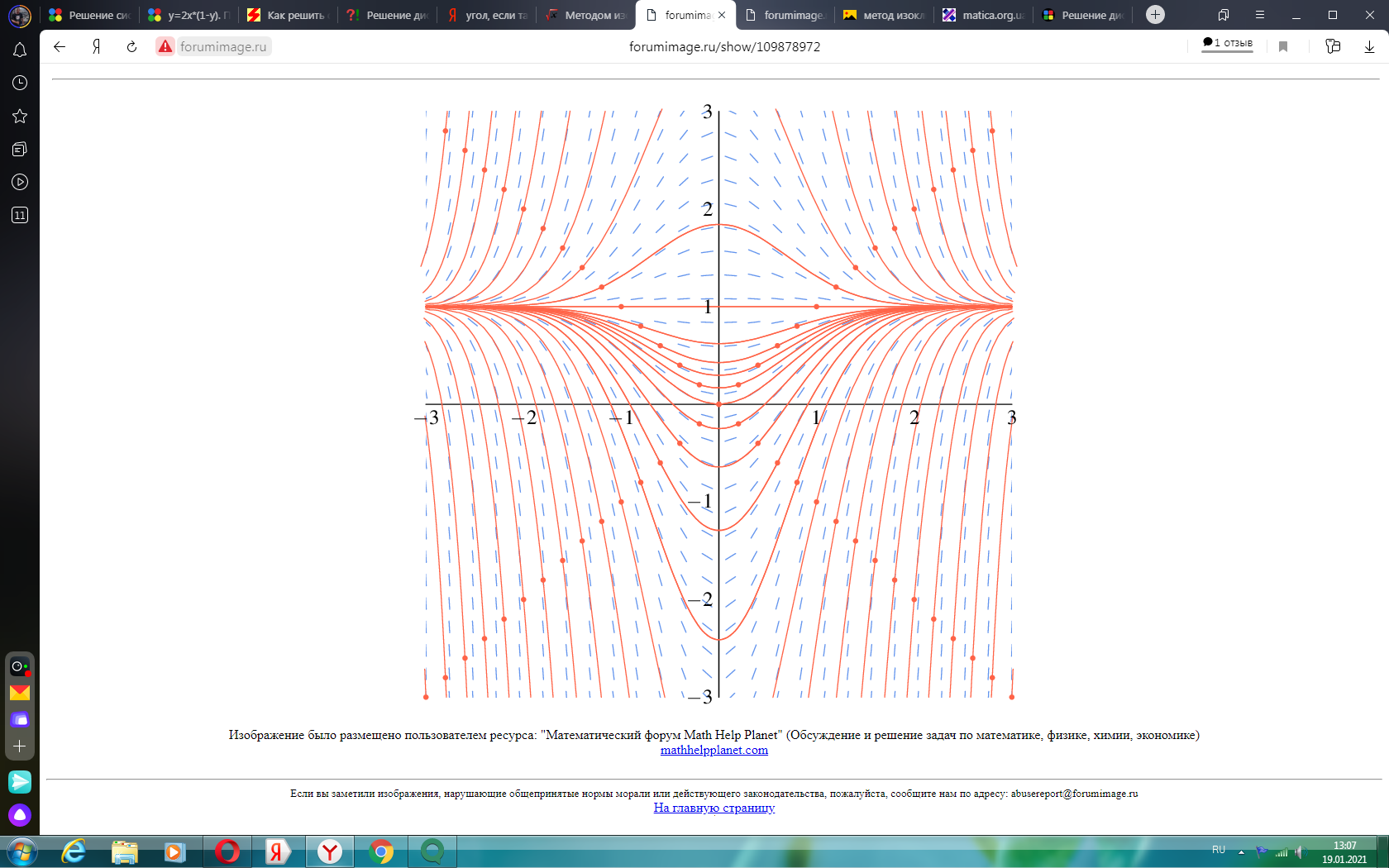 2. Решить уравнение, допускающее понижения порядка 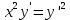 Решение: Один раз интегрируем обе части уравнения. 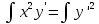 ⇒ ⇒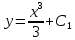 Ответ: 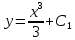 3. Решить систему уравнений. 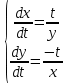 Решение: Выразим x из второго уравнения системы 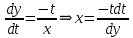 Дифференцируем по t обе части полученного уравнения 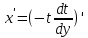 ⇒y'= ⇒y'=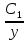 ⇒y'= ⇒y'=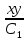 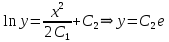 Ответ: 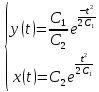 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение: По условию p=0,7, поэтому q=1 - 0,7 = 0,3 Для того, чтобы найти n, необходимо применить двойное неравенство p*n - q≤m≤p*n + p. Подставляем в неравенство исходные данные. 0,7n - 0,3≤10≤0,7n + 0,7 Преобразуем двойное неравенство в систему неравенств. 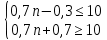 ⇒ ⇒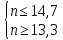 Ответ: необходимо провести 14 или 15 испытаний. |
