Теория анализа и статистика контрольная работа. Решение Найдем матрицу выручки по регионам обозначив ее буквой "С" С( ) ( ) ( ) 200 2 80 4 100 3 ( )
 Скачать 25.7 Kb. Скачать 25.7 Kb.
|
|
Вариант 7 1. Предприятие производит мебель трех видов и продает ее в четырех регионах. Матрица B=(bij)= ( 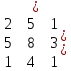 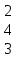 ) задает цены реализации единицы мебели i-го типа в j-м регионе. Найти выручку предприятия в каждом регионе, если реализация мебели за месяц (по видам) задана матрицей А=( ) задает цены реализации единицы мебели i-го типа в j-м регионе. Найти выручку предприятия в каждом регионе, если реализация мебели за месяц (по видам) задана матрицей А=(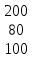 ) )Решение: Найдем матрицу выручки по регионам обозначив ее буквой "С" С=( 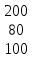 ) ) ( ( 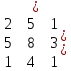 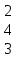 ) = ( ) = (  ) = ) = 200 *2 + 80 * 4 + 100 * 3 =( 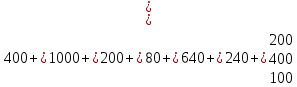 ) = ) =  400 + 320 + 300 1020 Таким образом выручка предприятия в 1-м регионе составляет 680, во втором регионе 2040, в третьем регионе 540, в четвертом регионе 1020 2. Дана матрица S полных затрат некоторой модели межотраслевого баланса S =( 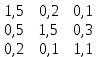 ) )Найти: а)приращение валового выпуска ∆X1, обеспечивающее приращение конечной продукции ∆Y1= ( 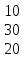 ); б) приращение конечной продукции ∆Y2, соответствующее приращению валового выпуска ∆X2 = ( ); б) приращение конечной продукции ∆Y2, соответствующее приращению валового выпуска ∆X2 = (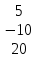 ) )Решение: ∆X= (S)*( ∆Y) (1) где ∆X -матрица приращения валового выпуска S - матрица полных затрат; ∆Y - матрица приращения конечной продукции (S-1)*( ∆X) = (S-1)*(S)*( ∆Y) (S-1) )*( ∆X)= ( ∆Y) ( ∆Y)= (S-1) *( ∆X) (2) где S-1- матрица, обратная к матрице полных затрат Таким образом, исходя из формул (1) и (2): (∆X1)=(S)*( ∆Y1) ( ∆Y2)= (S-1) *( ∆X2) Преобразим: (∆X1)=( 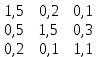 )* ( )* (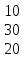 ) =( ) =( 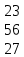 ) )( ∆Y2) = (S-1) * ( 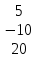 ) = ( ) = (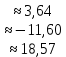 ) )3. Объем производства зимней обуви u 9ед.), выпускаемой некоторой фирмой, может быть описан уравнением u=1/3*t3-7/2*t2+6*t+ 2100 (ед), где t - календарный месяц года. Вычислить производительность труда, скорость и темпы ее изменения: а)в начале года (t=0); б)в конце года (t=12) Решение: Производительность труда выражается производной z(t) = u '(t) z(t) =(1/3*t3-7/2*t2+6*t+ 2100) ' = t2- 7t+6 (ед/мес) Скорость изменения производительности является производной производительности труда z'(t) z'(t) = ( t2- 7t+6) '= 2t-7 (ед/мес2) Темп изменения производной равен логарифму произврдной T= 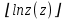 '= '= 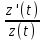 Tz(t)= 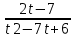 (ед/мес) (ед/мес)В заданные моменты времени соответственно имеем: а)t=0,z(0) = 6 (ед/мес) z'(0) = -7 (ед/мес2) Тz(0) = 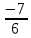 = -1,167(ед/мес) = -1,167(ед/мес)б) t = 12 z(12)= 122- 7*12+6=144-84+6=66(ед/мес) z'(12)= 2*12-7= 17(ед/мес2) Тz(12) = 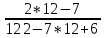 = 3,882(ед/мес) = 3,882(ед/мес)4. Задана производственная функция, цены единицы первого и второго ресурсов, а так же ограничения I в сумме, которая может быт потрачена на приобретение ресурсов (сумма 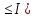 . Найти величины используемых ресурсов (x,y), при которых фирма-производитель получит наибольшую прибыль: . Найти величины используемых ресурсов (x,y), при которых фирма-производитель получит наибольшую прибыль:K(x,y) = 24* 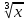 * *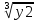 ; p1=27, p2=4, I = 6 ; p1=27, p2=4, I = 6Решение: Производственная функция в денежном выражении равна доходу от использования ресурсов, так как функция C(x)=p1*x+p2*y, следовательно C(x)= 27x+4y Таким образом функция прибыли равна П(x)= D(x)-C(x) П(x,y)= 24* 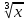 * *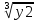 - 27x-4y - 27x-4y Вычислим наибольшее значение функции П(x,y)= 24* 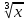 * *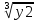 - 27x-4y = 24x1/3*y2/3- 27x-4y в области - 27x-4y = 24x1/3*y2/3- 27x-4y в области 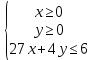 , т.е внутри и на и на границах треугольника с вершинами (0, 0), (2/9, 0), (0, 3/2). , т.е внутри и на и на границах треугольника с вершинами (0, 0), (2/9, 0), (0, 3/2).Для начала произведем расчет координат стационарных точек данной функции 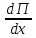 = 8x-3/2*y2/3 - 27, = 8x-3/2*y2/3 - 27,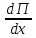 = 16x1/2*y-1/3 - 4. = 16x1/2*y-1/3 - 4.Из необходимых условий экстремума получим 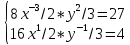 Выведем из нижнего уравнения системы y2/3=16x2/3, подставив в верхнее уравнение системы получаем:8x-2/3*16x2/3= 27; 128=27, что неверно означает, что у данной функции нету стационарных точек. Вычислим значения функции на границах области: Если x=0, то П(х,у)= -4y, П(0, 0) = 0, П(0, 3/2)= -6 Если y=0, то П(x, y)= -27x, П(0,0) = 0, П(2/9, 0)=-6 Если 27x+4y=6, то y = - 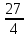 x+ x+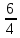 П(x, y) = П (х)= 24x1/3(- 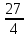 x+ x+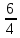 )2/3-27x-4((- )2/3-27x-4((-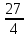 x+ x+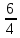 )= 24 )= 24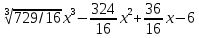 Вычислим координату стационарной точки: П'(x)= 0, 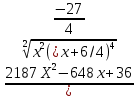 = 0, = 0, Решив верхнее уравнение через дискриминант мы получим х1=2/27 , x2= 2/9, из которых только первая удовлетворяет нижнему неравенству системы. Значит, стационарной является точка х=2/27, в которой функция принимает значение П(2/27)= 8 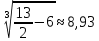 При этом y = -27/4*2/27+6/4=1 Исходя из вышеуказанного, фирма-производитель получит наибольшую прибыль при x= 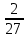 , y=1 , y=15.Стоимость перевозки 1 т груза на 1 км (тариф перевозки) задается функцией F(x)= 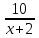 (ден, ед/км). Определить затраты на перевозку 1 т груза на расстоянии 20 км. (ден, ед/км). Определить затраты на перевозку 1 т груза на расстоянии 20 км.Ответ:23,98 ден/ ед |
