Вышмат-1_Задание_1_Вариант_14-1-12. Решение Найдем решение уравнения Находим определитель и получаем Таким образом, получаем собственные значения
 Скачать 60.41 Kb. Скачать 60.41 Kb.
|
Раздел 1. Линейная алгебраЗадание 1.14Определить собственные значения и собственные векторы матрицы третьего порядка. 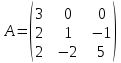 Решение: Найдем решение уравнения: 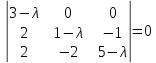 Находим определитель и получаем: 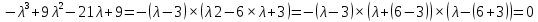 Таким образом, получаем собственные значения: 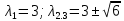 Для каждого λ найдем его собственные векторы: 1. 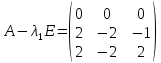 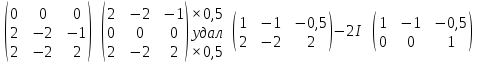 Таким образом, 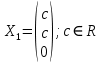 1. 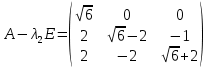 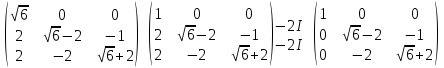 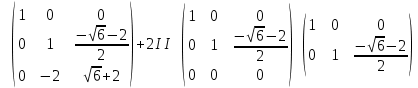 Таким образом, 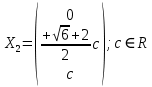 3. 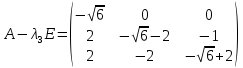 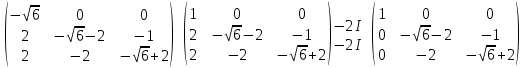 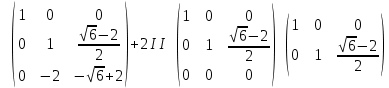 Таким образом, 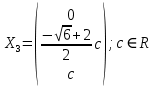 Задание 2.1Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления. 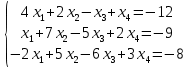 Решение: По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что бы ранг основной матрицы. Так как rang|A|=3 равен rang|B|=3, но меньше количества неизвестных n=4, то система имеет множество решений. В таком случае следует использовать метод Гаусса. 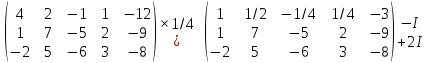 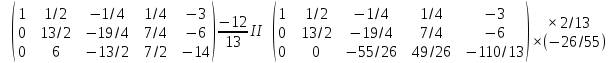 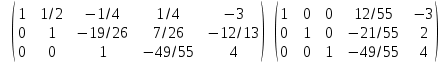 Ответ: 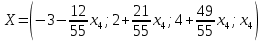 Решение в векторном виде: 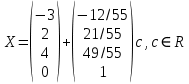 Задание 3.12Исследовать и найти общее решение системы линейных однородных уравнений. 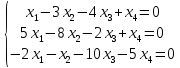 Решение: Рассмотрим основную матрицу и с помощью преобразований Гаусса получим эквивалентную ей с точки зрения решений системы: 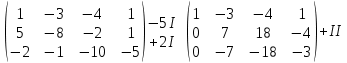 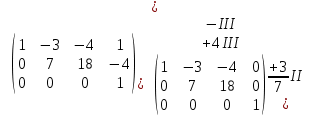 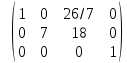 Получаем эквивалентную систему и решение системы: 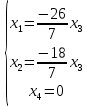 Ответ: 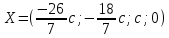 - общее решение системы. - общее решение системы.Раздел 2. Векторная алгебраЗадание 1.14Составить уравнение плоскости Р, проходящей через точку А перпендикулярно вектору 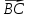 . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости 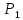 , проходящей через точки А, В, С. Найти угол между плоскостями P и P1. Найти расстояние от точки D до плоскости Р. , проходящей через точки А, В, С. Найти угол между плоскостями P и P1. Найти расстояние от точки D до плоскости Р.A=(1;0;2); B=(-2;0;6); C=(-3;1;2); D=(-1;2;4). Решение: Вектор 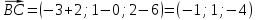 Найдем уравнение плоскости P: 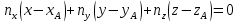 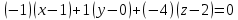 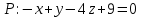 Найдем уравнение плоскости P1: 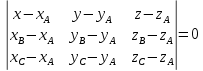 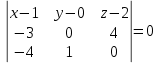 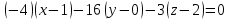 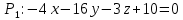 Вычислим угол между плоскостями: 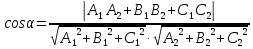 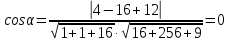 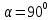 Найдем расстояние от точки D до плоскости P: 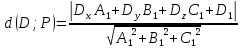 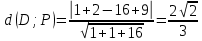 Задание 2.1Прямая l задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой l1, проходящей через точку М параллельно прямой l, и вычислить расстояние между ними. Найти проекцию точки М на прямую l и точку пересечения прямой l и плоскости Р. 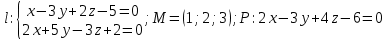 Решение: Находим направляющий вектор прямой: 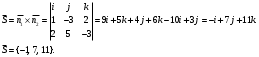 Находим точку прямой, приравняв нулю одну из координат: 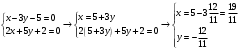 тогда каноническое уравнение имеет вид: 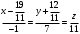 Параметрическое уравнение прямой 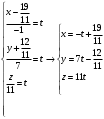 Составить уравнение прямой l1 , проходящей через точку М параллельно прямой l. 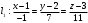 Вычислим расстояние между ними. Находим точки прямых: M1(19/11; 12/11; 0) и точка М(1; 2; 3). Вычислим координаты вектора М1М 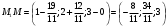 Находим векторное произведение 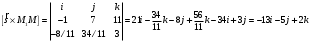 Тогда расстояние равно: 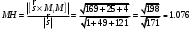 Находим проекцию точки М на прямую l, для этого находим плоскость, проходящую через эту точку с нормальным вектором s 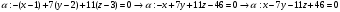 Находим точку пересечения плоскости и прямой. Записываем параметрическое уравнение прямой Находим точку пересечения плоскости и прямой. Записываем параметрическое уравнение прямой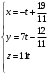 и подставим в уравнение плоскости и подставим в уравнение плоскости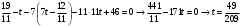 Вычисляем искомые координаты пересечения точки 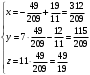 Тогда точка пересечения 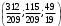 Находим точку пересечения плоскости и прямой. Записываем параметрическое уравнение прямой 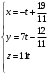 и подставим в уравнение плоскости P и подставим в уравнение плоскости P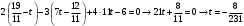 Вычисляем искомые координаты пересечения точки 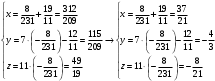 Тогда точка пересечения 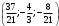 Раздел 3. Аналитическая геометрияЗадание 1.12Даны координаты вершин треугольника АВС. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла А, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам. A=(1;2); B=(3;4); C=(-1;2) Решение: Найдем соответствующие векторы: AB=(2;2); AC=(-2;0); BC=(-4;-2). Составим уравнения сторон треугольника: 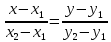 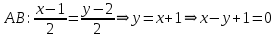 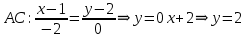 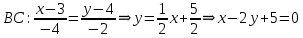 Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам: 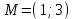 Найдем уравнение медианы: 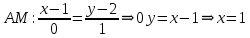 Найдем длину медианы: 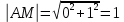 Найдем уравнение высоты AH. Она перпендикулярна прямой 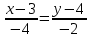 и проходит через A, т.е., имеет вид: и проходит через A, т.е., имеет вид: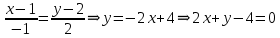 Найдем длину высоты: 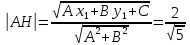 Найдем биссектрису угла A. Точку пересечения биссектрисы со стороной BC обозначим K. Уравнение AB: y=x+1, уравнение AC: y-2=0. 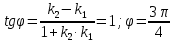 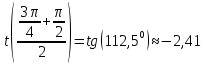 Уравнение биссектрисы имеет вид: 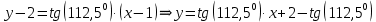 Уравнение прямой, параллельной BC, проходящей через точку A: 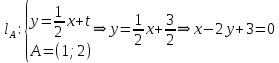 Уравнение прямой, параллельной AC, проходящей через точку B: 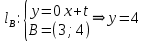 Уравнение прямой, параллельной AB, проходящей через точку C: 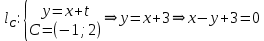 Задание 2.14По координатам вершин пирамиды АВСD средствами векторной алгебры найти: 1) длины ребер АВ и АС; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) проекцию вектора AB на AC; 5) объем пирамиды. A=(3;-5;2); B=(4;5;1); C=(-3;0;-4); D=(-4;5;-6). Решение: Составим уравнение векторов при точке A: 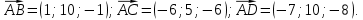 Найдем длины векторов: 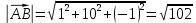 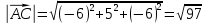 Найдем угол между ребрами АВ и АС как угол между соответствующими векторами: 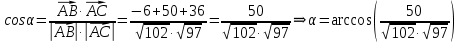 Площадь грани АВС найдем как площадь треугольника через векторное произведение векторов AB и AC: 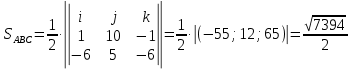 Найдем проекцию вектора AB на AC: 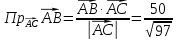 Найдем объем пирамиды, используя смешанное произведение: 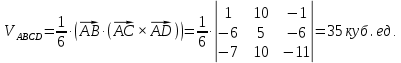 |
