Математика. 1 вариант 22.04.21. Решение Найдем решение задачи аналитическим методом

• Название: Решение Найдем решение задачи аналитическим методом
• Анкор: Математика
• Дата: 02.01.2022
• Размер: 180.5 Kb.
• Имя файла: 1 вариант 22.04.21.docx
• Тип: Решение; #323034

Содержание

Задание 1 2

Задание 2 6

Задание 3 9

Задание 4 12

Список использованных источников 14

Задание 1

Условие:

Найти решение игры, заданной матрицей А:

а) аналитическим методом;

б) графическим методом.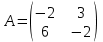


Решение:

Найдем решение задачи аналитическим методом.

Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.

Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B1	B2	a = min(Ai)
A1	-2	3	-2
A2	6	-2	-2
b = max(Bi)	6	3

Находим гарантированный выигрыш, определяемый нижней ценой игры

a = max(a_i) = -2, которая указывает на максимальную чистую стратегию A₂.

Верхняя цена игры b = min(b_j) = 3.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -2 ≤ y ≤ 3. Находим решение игры в смешанных стратегиях. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).

Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.

Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.

Находим решение игры в смешанных стратегиях.

Запишем систему уравнений.

Для игрока I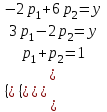



Для игрока II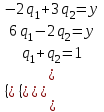



Решение найдем по следующим формулам: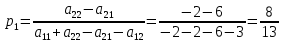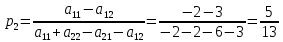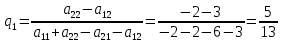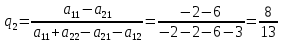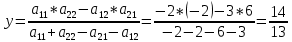











p₁ = ⁸/₁₃ (вероятность применения 1-ой стратегии).

p₂ = ⁵/₁₃ (вероятность применения 2-ой стратегии).

Оптимальная смешанная стратегия игрока I: P = (⁸/₁₃; ⁵/₁₃)

q₁ = ⁵/₁₃ (вероятность применения 1-ой стратегии).

q₂ = ⁸/₁₃ (вероятность применения 2-ой стратегии).

Оптимальная смешанная стратегия игрока II: Q = (⁵/₁₃; ⁸/₁₃)

Цена игры: y = 14/13

Решим задачу геометрическим методом, который включает в себя следующие этапы:

В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A₁, правый - стратегии A₂ (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S₁ = (p₁,p₂).

На левой оси ординат откладываются выигрыши стратегии A₁. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A₂.

Решение игры (2 x 2) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.

Выделяем нижнюю границу выигрыша B₁NB₂, рисунок 1.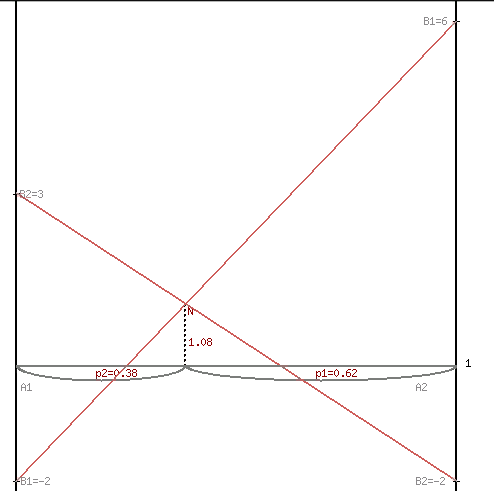


Рисунок 1 – Графическое решение

Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B₁B₁ и B₂B₂, для которых можно записать следующую систему уравнений: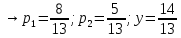



Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений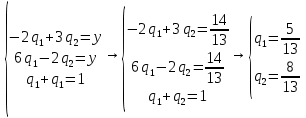

Задание 2

Условие:

Найти графическим методом решение игры, заданной матрицей.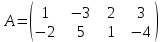


Решение:

 Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B1	B2	B3	B4	a = min(Ai)
A1	1	-3	2	3	-3
A2	-2	5	1	-4	-4
b = max(Bi)	1	5	2	3

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = -3, которая указывает на максимальную чистую стратегию A₁.

Верхняя цена игры b = min(b_j) = 1.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -3 ≤ y ≤ 1. Находим решение игры в смешанных стратегиях

Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.

С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₃ (все элементы столбца 1 меньше элементов столбца 3), следовательно, исключаем 3-й столбец матрицы. Вероятность q₃ = 0.

1	-3	3
-2	5	-4

В платежной матрице отсутствуют доминирующие строки.

свели игру 2 x 4 к игре 2 x 3.

Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.

Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.

В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A₁, правый - стратегии A₂ (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S₁ = (p₁,p₂).

На левой оси ординат откладываются выигрыши стратегии A₁. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A₂.

Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.

Выделяем нижнюю границу выигрыша B₁NB₂, рисунок 2.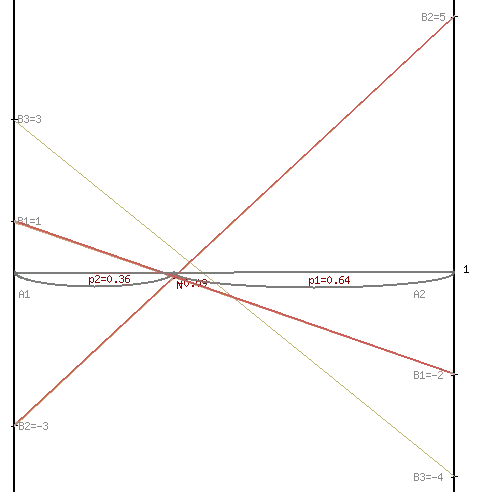


Рисунок 2 – Графическое решение
Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B₁B₁ и B₂B₂, для которых можно записать следующую систему уравнений: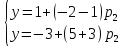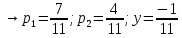



Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию В₃, которая дает явно больший проигрыш игроку В и следовательно q₃=0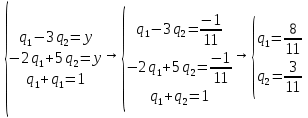

Задание 3

Условие:

По данным десяти наблюдений:

а) составить выборочное уравнение регрессии Y на Х;

б) построить корреляционное поле и линию регрессии;

в) сделать прогноз при х = х_α;

г) вычислить выборочный коэффициент корреляции и по нему оценить

тесноту и направление связи между признаками.

Xi	1	3	4	4	6	8	10	12	13	15
Yi	9	18	17	20	24	29	38	47	46	51

x_a=20
Решение:

Для расчета параметров регрессии построим расчетную таблицу 1
Таблица 1 – Расчетная таблица

x	y	x2	y2	x*y
1	9	1	81	9
3	18	9	324	54
4	17	16	289	68
4	20	16	400	80
6	24	36	576	144
8	29	64	841	232
10	38	100	1444	380
12	47	144	2209	564
13	46	169	2116	598
15	51	225	2601	765
76	299	780	10881	2894

Выборочные средние.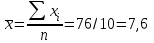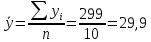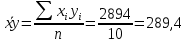

, ,

Выборочные дисперсии: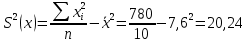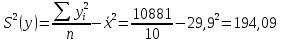





Среднеквадратическое отклонение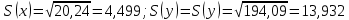



Коэффициент корреляции b можно находить по формуле: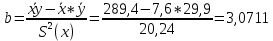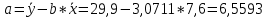





Тогда уравнение регрессии У на Х:

y=3,0711х+6,5593

Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = 3,0711 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 3,0711.

Коэффициент a = 6,559 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.

Сделаем прогноз при х=20

у=3,0711*20+6,5593=67,9813

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: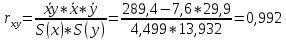



Линейный коэффициент корреляции принимает значения от –1 до +1.

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:

0.1 < r_xy < 0.3: слабая;

0.3 < r_xy < 0.5: умеренная;

0.5 < r_xy < 0.7: заметная;

0.7 < r_xy < 0.9: высокая;

0.9 < r_xy < 1: весьма высокая;

В нашем примере связь между признаком Y и фактором X весьма высокая и прямая.

На рисунке 3 представлено поле корреляции.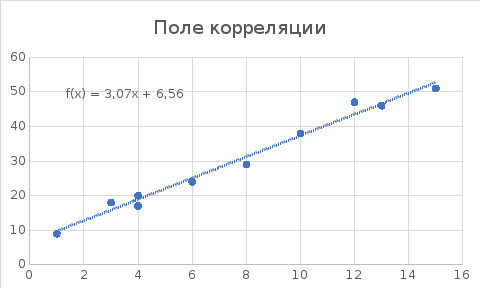

Рисунок 3 – Поле корреляции

Задание 4

Условие:

По данным n наблюдений вычислить выборочный коэффициент корреляции и составить уравнения прямых линий регрессии Y на Х и Х на Y.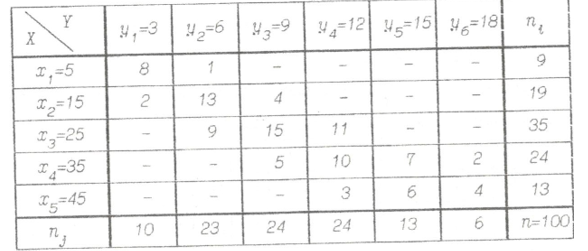


Решение:

Уравнение линейной регрессии с y на x имеет вид: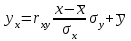



Уравнение линейной регрессии с x на y имеет вид: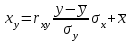



Найдем необходимые числовые характеристики.
Выборочные средние: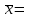

 (5(8 + 1) + 15(2 + 13 + 4) + 25(9 + 15 + 11) + 35(5 + 10 + 7 + 2) + 45(3 + 6 + 4))/100 = 26.3

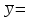(3(8 + 2) + 6(1 + 13 + 9) + 9(4 + 15 + 5) + 12(11 + 10 + 3) + 15(7 + 6) + 18(2 + 4))/100 = 9.75

Дисперсии:

σ²_x = (5²(8 + 1) + 15²(2 + 13 + 4) + 25²(9 + 15 + 11) + 35²(5 + 10 + 7 + 2) + 45²(3 + 6 + 4))/100 - 26.3² = 129.31

σ²_y =  (3²(8 + 2) + 6²(1 + 13 + 9) + 9²(4 + 15 + 5) + 12²(11 + 10 + 3) + 15²(7 + 6) + 18²(2 + 4))/100 - 9.75² = 16.81

Откуда получаем среднеквадратические отклонения:

σ_x = 11,371 и σ_y = 4,1

и ковариация:

Cov(x,y) = (5*3*8 + 15*3*2 + 5*6*1 + 15*6*13 + 25*6*9 + 15*9*4 + 25*9*15 + 35*9*5 + 25*12*11 + 35*12*10 + 45*12*3 + 35*15*7 + 45*15*6 + 35*18*2 + 45*18*4)/100 - 26.3*9.75 = 39.53

Определим коэффициент корреляции: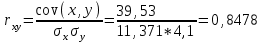



Запишем уравнения линий регрессии y(x):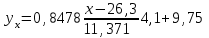



и вычисляя, получаем:

y_x = 0,31 x + 1,71

Запишем уравнения линий регрессии x(y):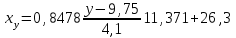



и вычисляя, получаем:

x_y = 2,35 y + 3,37

Список использованных источников

1. 
   Краснов, М.Л. Вся высшая математика. Т.5. Теория вероятностей, математическая статистика, теория игр / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. - М.: ЛКИ, 2015. - 296 c.
   
2. 
   Кочетыгов, А. А. Основы эконометрики / А.А. Кочетыгов, Л.А. Толоконников. - М.: Издательский центр "МарТ", 2015. - 352 c.
   
3. 
   Лабскер, Л.Г. Теория игр в экономике. Практикум с решениями задач (для бакалавров) / Л.Г. Лабскер; под ред. Ященко Н.А.. - М.: КноРус, 2016. - 331 c.
   
4. 
   Носко, В.П. Эконометрика. В 2-х т.Книга 1: Часть 1: Основные понятия, элементарные методы; Часть 2: Регрессионный анализ временных рядов: Учебник / В.П. Носко. - М.: ИД Дело РАНХиГС, 2011. - 672 c.