Математика. Решение Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)k, где kconst. Следовательно k2x(1y)
 Скачать 59.64 Kb. Скачать 59.64 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА Группа Студент МОСКВА 2020 Методом изоклин построить интегральные кривые уравнения:  Решение: Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)=k, где k=const. Следовательно k=2x(1-y)⇔1-y=k/2x⇔y=1-k/2x Изоклины представляют собой семейство гипербол. При k=0 имеем y=1 и tgα=k⇔tgα=0⇔α=0° При k=1 имеем y=1-1/2x и tgα=1⇔α=45° При k=-1 имеем y=1+1/2x и tgα=-1⇔α=135° При k=2 имеем y=1-1/x и tgα=1⇔α≈63° При k=-2 имеем y=1+1/x и tgα=-1⇔α≈117° 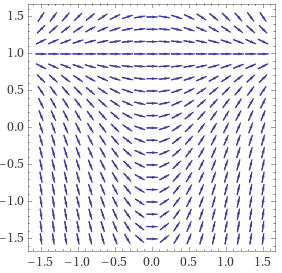 Решить уравнение, допускающее понижения порядка: x2y'' = y'2. Делаем замену y'=z(x). Тогда y''=z'(x). Подставляя в исходное уравнение, получаем x2z'=z2. Разделяя переменные, получаем  . .Интегрируя, имеем 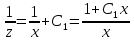 , или, что тоже самое, , или, что тоже самое, 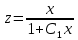 . .Последнее соотношение записывается в виде: 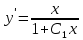 , откуда , откуда 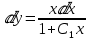 . .Интегрируя, окончательно получаем  . .Решить систему уравнений: 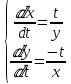  y*dx=-x*dy; dy/y=-dx/x; Ln(y(x))=C-Ln(x); Ответ: 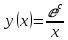 Пусть производится n опытов, вероятность наступления события A в каждом из которых одинакова равна p (p=0,7). Тогда наивероятнейшее число m (m=10) наступлений события A в этой серии опытов можно найти по формуле: np−q≤m≤np+p, q=1−p. q=1-0.7= 0.3 0.7*n−0.3≤10≤0.7*n+0.7 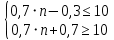 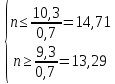 Ответ: Необходимо провести 14 или 15 испытаний. |
