Практическая по теории вероятностей. Практическое задание (теория вероятности). Решение Найдем вероятность выбора первой буквы Р Количество событий равно общему количеству букв, т е. 6

• Название: Решение Найдем вероятность выбора первой буквы Р Количество событий равно общему количеству букв, т е. 6
• Анкор: Практическая по теории вероятностей
• Дата: 17.04.2022
• Размер: 20.13 Kb.
• Имя файла: Практическое задание (теория вероятности).docx
• Тип: Документы; #480202

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА



Группа Уз20Э111
Студент
З.Э. Аблямитова


МОСКВА 2021

Задание №1
Буквы, составляющие слово РАКЕТА, написаны по одной на шести
карточках; карточки перемешаны и положены в пакет.

1. 
   Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА?
   
2. 
   Какова вероятность сложить слово КАРЕТА при вынимании всех букв?
   

1. 
   Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА?
   

Решение:

Найдем вероятность выбора первой буквы Р:

Количество событий равно общему количеству букв, т.е. 6.

Из них благоприятных событий (подходящих букв) равно 1.
Вероятность по формуле Лапласа: Р = .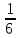

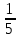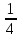Вероятность, что вторая буква Е: Р = (из остав. 5^ти букв 1 Е); Вероятность того, что третья буква будет К: Р = (из остав. 4^х букв 1 К);

Вероятность того, что четвертая буква будет А: Р = 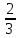(из остав. 3^х букв 2 А);

Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А: Р = .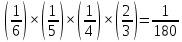
Ответ: Вероятность того, что, вынимая четыре буквы, получим слово РЕКА равна .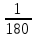


1.2 Какова вероятность сложить слово КАРЕТА при вынимании всех букв?
Решение:
Найдем вероятность выбора первой буквы К:

Количество событий равно общему количеству букв, т.е. 6.

Из них благоприятных событий (подходящих букв) равно 1.

Вероятность по формуле Лапласа: К = .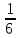

Вероятность, что вторая буква А: Р = 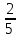(из остав. 5^ти букв 2 А);

Вероятность того, что третья буква будет Р: Р = 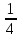(из остав. 4^х букв 1 Р);

Вероятность того, что четвертая буква будет Е: Р = 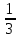(из остав. 3^х букв 1 Е);

Вероятность того, что пятая буква будет Т: Р = 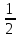(из остав. 2^х букв 1 Т);

Вероятность того, что шестая буква будет А: Р = 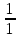(из остав. 1^х букв 1 А);

Вероятность взаимосвязанных событий, что поочередно вынуты буквы К, А, Р, Е, Т, А: Р = = .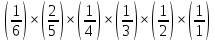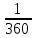
Ответ: Вероятность того, что, при вынимании всех букв буквы, получим слово КАРЕТА равна .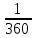
Задание №2
Дискретная случайная величина ξ задана следующим законом распределения:

ξ	4	6	10	12
р	0,4	0,1	0,2	0,3

Найти математическое ожидание, дисперсию и среднее квадратическое
отклонение.
Решение:
Математическое ожидание M[ξ]. M[ξ] = 4 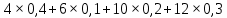= 7,8

Дисперсия D[ξ]. D[ξ] = 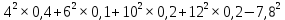= 73,2 – 60,84 = 12,36
Среднее квадратическое отклонение σ(ξ).

Среднее квадратическое отклонение σ(ξ).

σ (ξ)=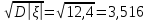
Ответ:  M[ξ] = 7,8; D[ξ] = 12,36; σ (ξ)= 3,516.


Задание 3
Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание M[ξ] = 1.9, а также
M[ξ]² = 7.3, найти вероятности 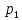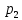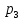_{, , ,} которые соответствуют дискретным значениям случайной величины.
Решение:


Так как:

M[ξ] = -2р₁ + р₂ +4 р₃ = 1,9; M[ξ²] = 4р₁ + р₂ +16 р₃ = 7,3 и р₁ + р₂ + р₃=1, то получим: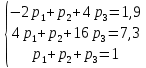

Ранг матрицы системы равен рангу расширенной матрицы, значит, система совместна. Тогда получим:

18р₃ =7,2, тогда р₃ = 0,4

3р₂ = 3,9 – 6 * 0,4, тогда р₂ = 0,5

р₁ = 1 - 0,5 – 0,4, тогда р₁ = 0,1.
Ответ: р₁ = 0,1; р₂ = 0,5; р₃ = 0,4.