Оптимизация решений 5й вариант. Оптимизация решений. Решение Необходимо найти максимальное значение целевой функции f 2x 1 4x 2

• Название: Решение Необходимо найти максимальное значение целевой функции f 2x 1 4x 2
• Анкор: Оптимизация решений 5й вариант
• Дата: 18.08.2020
• Размер: 55.86 Kb.
• Имя файла: Оптимизация решений.docx
• Тип: Решение; #135741
• страница: 1 из 4

Вариант 5
1. Решить графическим методом задачу ЛП. Найти максимум и минимум функции F(x) = -2x₁ + 4x₂

при ограничениях

x₁ + 2x₂  5

-3x₁ +2x₂  9

x₁ + 3x₂  6

x₁ 0, x₂ 0
Решение:
Необходимо найти максимальное значение целевой функции
F = -2x₁+4x₂ → max при системе ограничений:

x₁+2x₂≤5, (1)
-3x₁+2x₂≤9, (2)
x₁+3x₂≥6, (3)
x₁ ≥ 0, (4)
x₂ ≥ 0, (5)

Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение x₁+2x₂ = 5 по двум точкам. Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 2.5. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 5. Соединяем точку (0;2.5) с (5;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 ∙ 0 + 2 ∙ 0 - 5 ≤ 0, т.е. x₁+2x₂ - 5≤ 0 в полуплоскости ниже прямой.

Построим уравнение -3x₁+2x₂ = 9 по двум точкам. Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 4.5. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = -3. Соединяем точку (0;4.5) с (-3;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:
-3 ∙ 0 + 2 ∙ 0 - 9 ≤ 0, т.е. -3x₁+2x₂ - 9≤ 0 в полуплоскости ниже прямой.

Построим уравнение x₁+3x₂ = 6 по двум точкам. Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 2. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 6. Соединяем точку (0;2) с (6;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 ∙ 0 + 3 ∙ 0 - 6 ≤ 0, т.е. x₁+3x₂ - 6≥ 0 в полуплоскости выше прямой.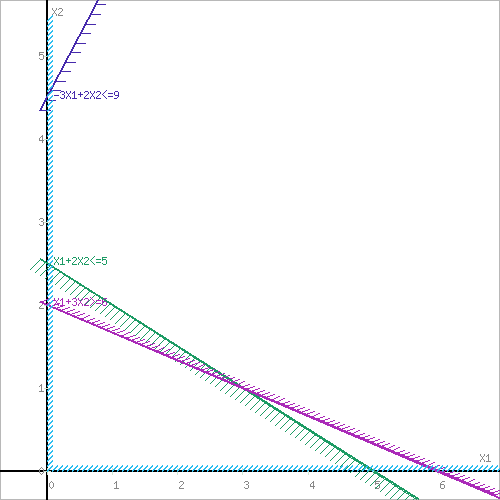


Шаг №2. Границы области допустимых решений.

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.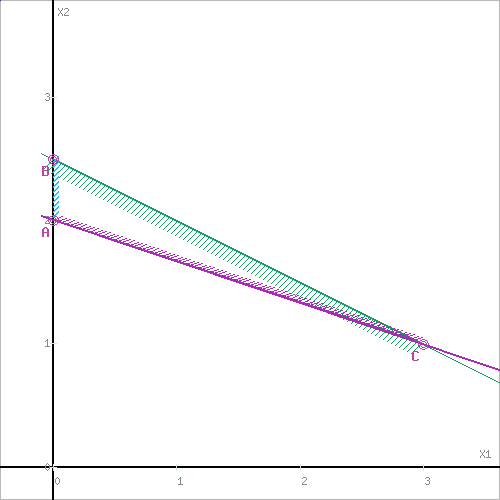


Шаг №3. Рассмотрим целевую функцию задачи F = -2x₁+4x₂ → max.

Построим прямую, отвечающую значению функции F = -2x₁+4x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (-2;4). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.


Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (4), то ее координаты удовлетворяют уравнениям этих прямых:

x₁+2x₂=5
x₁=0

Решив систему уравнений, получим: x₁ = 0, x₂ = 2.5.

Откуда найдем максимальное значение целевой функции:

F(X) = -2∙0 + 4∙2.5 = 10.

Шаг №4. Рассмотрим целевую функцию задачи F = -2x₁+4x₂ → min.
Построим прямую, отвечающую значению функции F = -2x₁+4x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (-2;4). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.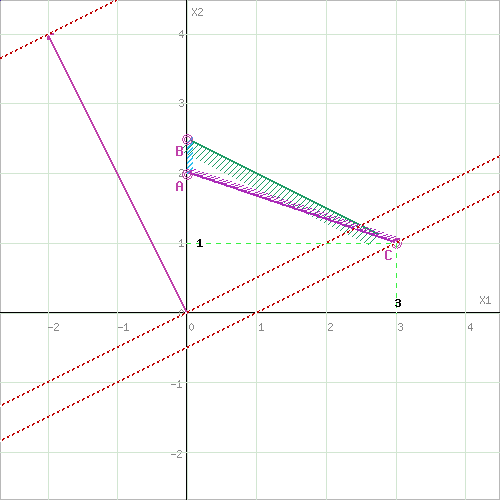

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

x₁+2x₂=5
x₁+3x₂=6

Решив систему уравнений, получим: x₁ = 3, x₂ = 1.

Откуда найдем минимальное значение целевой функции:

F(X) = -2∙3 + 4∙1 = -2.

2. Решите транспортную задачу методом потенциалов

	30	25	15	20
40	4	3	6	4
30	1	6	2	8
20	2	4	5	7

Решение:
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

∑a = 40 + 30 + 20 = 90
∑b = 30 + 25 + 15 + 20 = 90

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.

Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен c₂₁=1. Для этого элемента запасы равны 30, потребности 30. Поскольку минимальным является 30, то вычитаем его.
x₂₁ = min(30,30) = 30.

4	3	6	4	40
1	x	x	x	30 - 30 = 0
2	4	5	7	20
30 - 30 = 0	25	15	20

Искомый элемент равен c₁₂=3. Для этого элемента запасы равны 40, потребности 25. Поскольку минимальным является 25, то вычитаем его.
x₁₂ = min(40,25) = 25.

4	3	6	4	40 - 25 = 15
1	x	x	x	0
2	x	5	7	20
0	25 - 25 = 0	15	20

Искомый элемент равен c₁₄=4. Для этого элемента запасы равны 15, потребности 20. Поскольку минимальным является 15, то вычитаем его.
x₁₄ = min(15,20) = 15.

4	3	x	4	15 - 15 = 0
1	x	x	x	0
2	x	5	7	20
0	0	15	20 - 15 = 5

Искомый элемент равен c₃₃=5. Для этого элемента запасы равны 20, потребности 15. Поскольку минимальным является 15, то вычитаем его.
x₃₃ = min(20,15) = 15.

4	3	x	4	0
1	x	x	x	0
2	x	5	7	20 - 15 = 5
0	0	15 - 15 = 0	5

Искомый элемент равен c₃₄=7. Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x₃₄ = min(5,5) = 5.

4	3	x	4	0
1	x	x	x	0
2	x	5	7	5 - 5 = 0
0	0	0	5 - 5 = 0

Далее, согласно алгоритму, ищем элементы среди не вычеркнутых.

4	3	6	4	40
1	6	2	8	30
2	4	5	7	20
30	25	15	20

Искомый элемент равен c₂₃=2, но т.к. ограничения выполнены, то x₂₃=0.

	B1	B2	B3	B4	Запасы
A1	4	3[25]	6	4[15]	40
A2	1[30]	6	2[0]	8	30
A3	2	4	5[15]	7[5]	20
Потребности	30	25	15	20

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть
m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 3*25 + 4*15 + 1*30 + 5*15 + 7*5 = 275