Конспект урока математики в 9 классе _Метод интервалов. Решение. Решение неравенств методом интервалов
 Скачать 34.7 Kb. Скачать 34.7 Kb.
|
|
Тема урока: «Решение неравенств методом интервалов» Деятельностная цель: формирование умений применением метода интервалов при решении простейших неравенств с кратными корнями. Содержательная цель: расширение знаний учащихся и рассмотреть применение метода интервалов для решения неравенств различных типов. Задачи урока: 1. Сформировать у школьников мотивацию к изучению данной темы. 2. Формировать умения применять полученные знания на практике, в новых условиях; 3.Содействовать развитию познавательного интереса к предмету, внимания, памяти; Тип урока: урок «открытия» нового знания Форма занятия: урок – игра «Путешествие» Оборудование и материалы: компьютер, проектор, экран, презентация для сопровождения занятия, раздаточный материал для учащихся. Ход урока I.Организационный момент – Здравствуйте, ребята! Сегодня вы сделаете очередной шаг навстречу большой цели – итоговая аттестация. Я с радостью помогу вам сделать этот шаг. Однажды я прочла высказывание «Получать готовую информацию и запоминать ее может компьютер, а человек должен думать». – Пусть эти слова будут эпитетом к нашему уроку. А урок у нас не совсем обычный. Каждый из нас согласно основному закону страны, «Конституции РФ», имеет право на образование и право на свободное перемещение. Сегодня мы с вами отправимся в математическое путешествие. - У себя на столах вы можете найти вспомогательные материалы для работы. - Итак, начнем наше путешествие: вам необходимо пройти регистрацию и ознакомиться с проблемными вопросами, решением которых мы будем заниматься в ходе нашего путешествия - Приготовьте свои посадочные карточки. Листы оценивания. 2. Устная работа 1 этап регистрация: «Тест контроль» І вариант 1) Разложение на множители квадратного трехчлена х2 + 6х + 9 имеет вид: а) (х + 2)(х – 3); б) (х + 3)2; в) (х – 3)2. 2) Корнями уравнения (х – 2)(х + 10) = 0, являются: а) 2 и 10; б) 2 и – 10; в) – 2 и 10. 3) Изображение на координатной прямой корней уравнения (х + 2)(х – 7) = 0 а    ) ) -7 2 б    ) ) -2 7 в    ) ) -7 -2 ІІ вариант 1) Разложение на множители квадратного трехчлена х2 – 8х + 16 имеет вид: а) (х + 2)(х – 8); б) (х + 4)2; в) (х – 4)2. 2) Конями уравнения (х + 2)(х – 5) = 0, являются: а) 2 и 5; б) 2 и – 5; в) – 2 и 5. 3) Изображение на координатной прямой корней уравнения (х – 4)(х – 11) = 0: а    ) ) -4 11 б    ) ) -11 -4 в    ) ) 4 11 Ответы: І вариант все б); ІІ вариант все в). Ребята обмениваются регистрационными карточками, проверяют их, производят оценивание: за каждый правильный ответ на вопросы теста по 1 баллу (всего 3 балла). 2 этап: Изучение нового материала. Первая станция «Круг идей» Фронтальная работа с классом. Учитель: Перед нами стоит задача. Надо решить неравенство (х – 4) (х + 1)>0. Учитель: Когда произведение двух выражений положительно? Уч-ся: Если оба сомножителя одновременно положительны или одновременно отрицательны. Значит, нужно решить две системы неравенств: 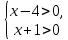 2) 2)  Два ученика у доски, остальные самостоятельно. - Решением первой системы будет промежуток (4; +∞), а решением второй – промежуток (-∞; -1). Таким образом, получаем, что решением исходного неравенства будет объединение этих промежутков, то есть x∈(-∞; -1)∪ (4; +∞). Учитель: Приемлем ли такой способ решения неравенств подобного вида? Уч-ся: Да. Учитель: А если нам потребуется решить неравенство (x + 5)(x + 4)(x – 5) < 0 А для этого неравенства такой способ решения удобен? Уч-ся: Не совсем. Учитель: Итак, для решения второго неравенства необходимо искать другой способ. Учитель: Назовите нули функции Уч-ся: Нули функции: х1= -5, х2 = -4, х3= 5. У   читель: Отметим их на координатном луче. - + - + читель: Отметим их на координатном луче. - + - +  Что они сделали с областью определения Что они сделали с областью определения -5 -4 5 х функции? Уч-ся: Они разбили область определения на промежутки (-∞; -5); (-5;-4); (-4;5); (5; +∞). Учитель: Выясним, каковы знаки функции в каждом из указанных промежутков. Для этого возьмем число из промежутка и подставим в неравенство. Мы видим, что в каждом из промежутков (-∞; -5); (-5;-4); (-4;5); (5; +∞) функция сохраняет знак, а при переходе через точки -5, -4, 5 её знак изменяется. 5. Выберем промежуток, соответствующий знаку неравенства ( «+» – знак >, « – » – знак <) x∈(-2; -1)∪ (2; +∞). Учитель: Итак, мы рассмотрели два метода решения неравенств. Какой метод более рациональный? Уч-ся: Метод интервалов. Сформулируйте тему нашего урока: Метод интервалов при решении неравенств с кратными корнями - Как вы думаете какие цели мы будем ставить в ходе нашего путешествия. -Научиться решать неравенства новым методом; расширить математический кругозор; учиться работать самостоятельно и в группе; проконтролировать уровень усвоения темы. - Итак, уважаемые пассажиры, вы прошли регистрацию и, считаю, готовы отправиться в путешествие. Учитель: Давайте попытаемся обобщить последний метод решения неравенств с одной переменной.
3 этап: Актуализация знаний Повторяем алгоритм решения неравенств методом интервалов. Решить неравенство (с проведением сравнительного анализа решения): (x – 5)(x + 4)(x + 5)2 ≤ 0. Вопросы: Как вы думаете будут сложности в решении данного неравенства? В чём они будут заключатся? - Что вы заметили при решении данных неравенств? (не чередуются знаки на интервалах в неравенстве ) Эта ситуация осложняет решение неравенств? (да, теперь знаки функции необходимо проверять на каждом интервале!) А может, есть способ, все- таки не менять привычный алгоритм решения? (возможно есть) (x – 5)(x + 4)(x + 5)2 ≤ 0 <=> (x - 5)(x+4) ≤ 0, x = - 5; Ответ. х € { - 5} U [- 4; 5] Прежде всего, отметим, что если в разложении многочлена на множители входит сомножитель  , то говорят, что , то говорят, что  - корень многочлена кратности - корень многочлена кратности 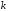 . . Значит, корень х = -5 кратности 2. 4 этап: Проблемное объяснение нового знания Итак, причина затруднения применения метода интервалов: не чередуются знаки на интервалах, что приводит к необходимости проверки знаков функции на каждом интервале. Решим неравенство: (x – 5)(x + 4)(x + 5)2 ≤ 0 другим способом: (x – 5)(x + 4)(x + 5)(x + 5) ≤ 0 Введем функцию f(x) = (x – 5)(x + 4)(x + 5)2; Д(f)=R. 1. Найдем нули функции f(x) = (x – 5)(x + 4)(x + 5)2, решив уравнение (х-5)(х+4)(х+5)2 = 0. x = 5; x = - 4; x = - 5 и x = - 5. - 5 – корень кратности 2 (две слившиеся точки), между ними интервал с началом и концом в точке -5. Давайте введем интервал с началом и концом в точке -5. (его длина равна 0) и на графике его изображают в виде лепестка. Количество лепестков равно k – 1 ( где к – это кратность корня). 2. Изобразим на координатной прямой нули функции не забывая про «лепестки». Нули функции разбивают область определения на интервалы, в каждом из которых функция непрерывна и сохраняет свой знак. Чередуя, расставим знаки в каждом интервале, учитывая «лепесток», т.е. интервал с началом и концом в точке-5, и по рисунку запишем решение исходного неравенства. Ответ: {-5} U [-4; 5] Надо менять алгоритм решения неравенств методом интервалов? Определять знаки функции на каждом интервале? Как поступать с кратными корнями? 5 этап: Первичное закрепление Отправляемся на станцию: «Обучая – учусь» Примеры: №1. Решить неравенство: (x – 1)(3 – x)4 (x – 2) < 0. Введем функцию f(x) = (x - 1)(3 –x)4 (x – 2), Д (f) = R. Нули функции: x =1; x =2; x =3 – корень кратности 4. Сколько «лепестков» рисуем в точке х=3? В точке х = 3 дорисуем 3 «лепестка». Определим знак функции f(x) на любом промежутке, например (-∞; 1) f(0) = (0 -1)(3 – 0) (0 -2) > 0, и, чередуя, проставим знаки. Ответ: (1; 2) U{3} № 2. Решить неравенство № 134 (а,б) с.44 На доске два ученика решают неравенства. Остальные работают в тетрадях. б) Работа в парах. Заполнить пропуски в карточке При решении неравенств с кратными корнями необходимо: 1. Найти ______________ функции f(х) = (х – х1)(х – х2) … (х – хп) 2. Изобразить на ____________________________________ функции. 3. В точках, которые являются кратными корнями, дорисовать нулевые интервалы в виде ______________________. 4. Количество лепестков равно _____________. 5. Определить ____________ функции на одном из интервалов и _________________ знаки на остальных интервалах, включая ________________. 6. При этом знаки____________________ на всех интервалах. 7. Записать _________________, в соответствии с условием. Заполнение проверить по слайду. Определить количество ошибок, расставляя знаки «+» или «- » Каждый получает карточку с алгоритмом. Ее вклеить в тетрадь. 6 этап: Физкультминутка Станция «Спортивная» 7 этап: Самостоятельна работа в группах. Следующая станция « Тайный конверт» Каждая пара получает закрытый конверт с заданием, аналогичным одному из рассмотренных примеров и решает поставленную задачу, затем в виде отчета эксперт записывает ответ на доске и объясняет его. Задания: А) 1) (х + 7)(х + 2)(4 – х)(2х – 10) ≥ 0. ( x Є [-7; -2] v [4; 5] ) 2) (х2 + 4х – 5)(х+7)(х + 3) ≥ 0 (х Є (- ∞; -7]v [-5; -3] v [1; + ∞) ) 3) (х + 4)(х + 1)(х – 1)(х – 8) ≥ 0 (х Є (- ∞; - 4] v [-1;1] ) Б) Самостоятельная работа (с взаимопроверкой в парах). Запишите три любых числа a, b, с, причем a < b < c и решите неравенство: (x – a)(x – b)2(x – c) ≥ 0. 7)Итоги самостоятельной работы Алгоритм решения неравенств с кратными корнями (х – х1)(х – х2)к … (х – хп)≥0 1. Найти нули функции f(х) = (х – х1)(х – х2)к … (х – хп) 2. Изобразить на координатной прямой нули функции. 3. В точках, которые являются кратными корнями, дорисовать нулевые интервалы в виде лепестков. 4. Количество лепестков равно k – 1 ( где к – это кратность корня). 5. Определить знаки функции на одном из интервалов и расставить знаки на остальных интервалах, включая «лепестки», чередуя знаки. 6. Записать ответ, в соответствии с условием. 8. Домашнее задание. Наше путешествие подошло к концу. Мы прибыли на станцию «Домашнее задание» Ваше домашнее задание нескольких уровне. Каждый выбирает уровень себе по силам. Начальный уровень І вариант Решить неравенство методом интервалов 1) (х + 1)(х – 2) > 0 2) х2 – 3х + 2 ≤ 0 3) (х – 4)/(х + 5) < 0 Начальный уровень ІІ вариант Решить неравенство методом интервалов 1) (х + 2)(х – 3) > 0 2) х2 – 3х – 4 ≤ 0 3) (х – 5)/(х +6) < 0 Средний уровень І вариант Решить неравенство методом интервалов 1) х2 – 7х + 12 ≤ 0 2) (х + 10)(х – 4) < 0 3) 2х (8 + х)(х – 12) > 0 4) (х + 2)(7 – х)(х – 13) 5) (х + 5)/(х - 6) >0 Средний уровень ІІ вариант Решить неравенство методом интервалов 1) х2 – 6х + 5 < 0 2) (х + 9)(х – 2) < 0 3) 4х (5 + х)(х – 8) > 0 4) (х + 9)(6 – х)(х – 10) ≤ 0 5) (х – 4)/(х + 7) > 0 Достаточный уровень І вариант Решить неравенство методом интервалов 1) (х – 2)(х +5)/(х + 2) ≥ 0 2) (х + 3)2(х + 1)(х – 2) ≤ 0 3) (16 – х2)(3х2 + 1) > 0 4) (6 – 3х)/(х + 4) ≥ 0 Достаточный уровень ІІ вариант Решить неравенство методом интервалов 1) (х + 1)(х – 9)/(х - 1) ≤ 0 2) (х + 2)(х – 1)(х – 3)2 ≤ 0 3) (25 – х2)(5х2 + 2) ≤ 0 4) (х + 4)/(10 - 2х) ≤ 0 Высокий уровень І вариант Решить неравенство методом интервалов 1) (х4 – 16х2)( - х2 – 5) ≤ 0 2) (– х2 + 8х – 7)/(х2 + х – 2) > 0 3) х3 – 5х2 + 6х ≥ 0 4) (х – 2)(х + 2)2(х + 3)/(х - 1) ≤ 0 Высокий уровень ІІ вариант Решить неравенство методом интервалов 1) (х4 – 25х2)( - х2 – 7) ≥ 0 2) (– х2 + 4х + 3)/( х2 – х – 2) < 0 3) х3 – 6х2 + 5х ≤ 0 4) (х – 3)(х + 3)2(х + 4)/(х - 2) ≥ 0 9.Итог урока. Станция «Рефлексия» Учитель: И вспомним начало нашего урока, ребята. Удалось ли за сегодняшний урок сделать чудные открытия? А какие открытия Вы для себя сделали? А какие цели урока мы ставили перед собой? Как Вы считаете, нам удалось достигнуть поставленных целей? Учитель: Ян Амос Коменский говорил: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию». Я надеюсь, что в сегодняшнем уроке вы найдете для себя хоть крупинку полезного. |
