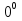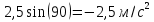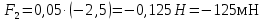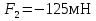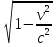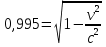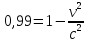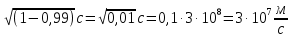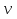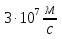         
1.75.Маховик начинает вращаться по закону . φ= 9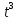 /32 рад Найти линейную скорость и ускорение точки, находящейся на расстоянии R= 0,8 м от оси вращения, в тот момент, когда её тангенциальное ускорение будет равно нормальному. Найти t1. /32 рад Найти линейную скорость и ускорение точки, находящейся на расстоянии R= 0,8 м от оси вращения, в тот момент, когда её тангенциальное ускорение будет равно нормальному. Найти t1.
Дано:
R=0,8м
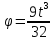
|
Решение.
Определим угловую скорость колеса как первую производную уравнения вращения:
w=(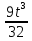 )/= )/=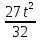
Определим угловое ускорение как вторую производную вращательного уравнения или первую производную угловой скорости:
ε=(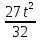 )/= )/=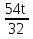
Нормальное ускорение в данный момент времени определим по формуле: аn=w2R=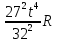
Тангенциальное ускорение определим по формуле:
aτ=εR=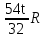
Приравниваем ускорения:
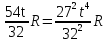
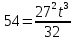 , t= , t=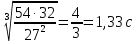
Линейная скорсоть равна:
V=wR=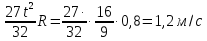
Ускорение равно:
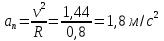
Тангенциальное ускорение:
aτ=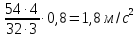
Полное ускорение а=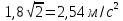
|
v-? a-? t-?
|
Ответ: t=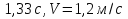 , а= , а=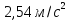
|
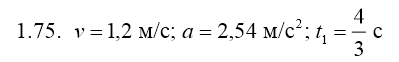
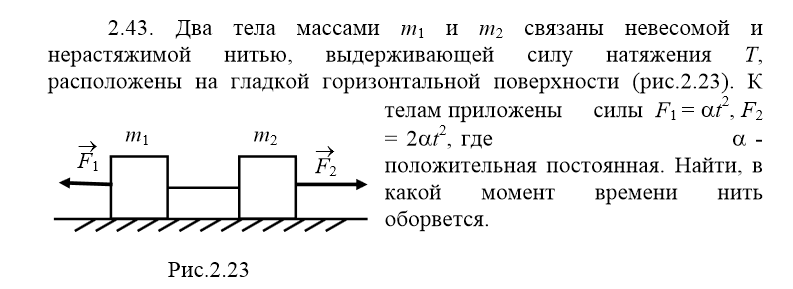
2.44. В условиях предыдущей задачи (2.43) найти скорость системы в момент обрыва нити, если при t = 0 v0 = 0.
Дано:
F1, F2, m1, m2,β, μ
|
Решение.
Указываем на чертеже силы, действующие a х
на каждое тело: F1 N1 N2 F2
Оси направим как на чертеже: Т
Для тела массой , m1 уравнения Ft1 Ft2
динамики в
проекциях на оси координат будут иметь вид:
OX: -F1 +T =m1 a (1)
OY: N1-Ft1 =0 (2)
Для тела второго уравнения в проекциях имеют вид:
OX: F2 -T -Fтр2=m2 a (3)
OY: N2-Ft2 =0 (4)
Сложим уравнения (1) и (3):
F2-F1 = (m1 + m2)
a=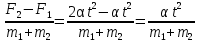
T-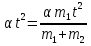 ,( ,( 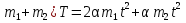
t=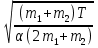
Ускорение а=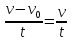
Отсюда находим скосроть:
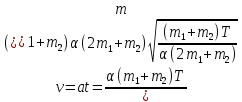
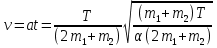
|
T-?
|
Ответ: 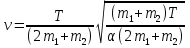
|
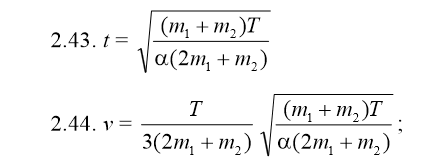
4.62. Математический маятник массы m и стержень массы M (рис.4.32) подвешены к точке А. Длина нити маятника l, длина стержня l. Маятник отклоняют, так что шарик поднимается на высоту h, Затем шарик отпускают и он сталкивается неупруго со стержнем. Как будут двигаться шарик и нижний конец стержня после удара и на какие высоты поднимутся? 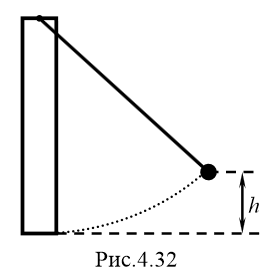
Дано:
l
M
Х=l
m
h
|
Решение.
Момент импульса маятника равен L1=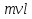 . Скорость пули найдём из формулы: . Скорость пули найдём из формулы: 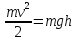 , , 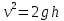 (1) (1)
После столкновения со стержнем момент импульса стержня равен моменту импульса пули по закону сохранения импульса, поэтому запишем: L=Jw2
Момент инерции стержня определим по формуле:
J=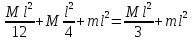 , , 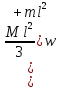 . .
Отсюда определим угловую скорость стержня:
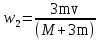
Найдём начальную кинетическую энергию стержня:
Wk=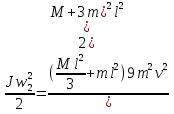 , учитывая (1), получаем: , учитывая (1), получаем:
Wk=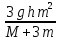
После того, как стержень поднялся на некоторую высоту, его кинетическая энергия превратилась в потенциальную энергию: 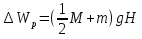 . .
По закону сохранения энергии
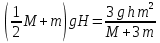
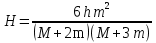
|
H-?
|
Ответ: 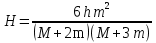
|

5.75. Найти центростремительное ускорение an, с которым движется по круговой орбите искусственный спутник Земли, находящийся на высоте h = 200 км от поверхности Земли.
Дано:
h,R,g0
|
Решение.
Ускорение силы тяжести на поверхности Земли равно: g=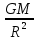 , ,
Отсюда определим величину: GM=g0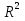 (1) (1)
ускорение силы тяжести на высоте h над поверхностью Земли определим по формуле:
g0=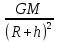 . (2) . (2)
Подставим в (2) формулу (1), получим:
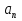 = =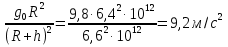 . .
|
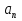 -? -?
|
Ответ: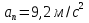
|
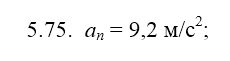
6.15. Написатьуравнение гармонического колебательного движения с амплитудой А = 50 мм, периодом Т = 4 с и ачальной фазой ϕ0 = π/4. Найти смещение x колеблющейся точки от положения равновесия при t = 0 и t = 1,5 c.
Дано:
А=50 мм
T=4c
φ0 = 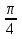
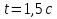
|
Решение.
Зная период колебаний, найдём циклическую частоту колебаний: w=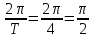 ; ;
Уравнение колебаний имеет вид:
Х=Аsin(wt+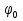 ). ).
Подставим известные величины: Х=50 sin(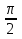 t+ t+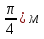 . .
Х1=50 sin(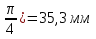
Х2=50 sin(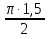 + +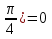
|
Х(t)-? 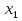 -? -?
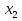 -? -?
|
Ответ: Х=0,1 соs(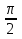 t+ t+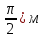 , Х1= , Х1=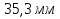 , Х2==0 , Х2==0
|
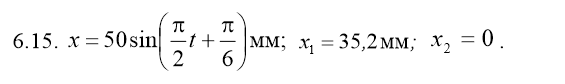
6.45. Материальная точка массой m = 0,05кг совершает гармонические колебания, уравнение которых имеет вид: x = 0,1 sin(5t) м Найти силу F действующую на точку 1) в момент, когда фаза колебания
ϕ = 30°, 2) в положении наибольшего отклонения точки.
Дано:
m=0,05
x =0,1sin5t, м
ϕ = 30°,
|
Решение.
Для определения скорости колебаний найдём производную :
V=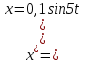
V=0,5cos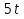 . .
Чтобы найти ускорение, найдём производную от скорости по времени:
а=V/=-2,5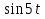
Найдём ускорение в момент времени для фазы ϕ = 30°:
а=-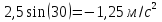
Силу в данный момент найдём по формуле:
F1=ma=0,05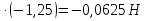 Н=-62,5мН Н=-62,5мН
В момент наибоьшего отклонения x =0,1sin5t
sin5t=1, 5t=9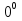
а=-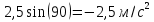
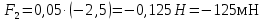
|
F-?
|
Ответ: F1=-62,5мН , 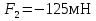
|
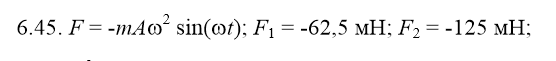
7.11. Стержень движется в продольном направлении с постоянной скоростью относительно инерциальной К-системы отсчета. При каком значении v длина стержня в этой системе отсчета будет на η = 0,5 % меньше его собственной длины?
Дано:
η=0, 5%
|
Решение.
Так как длина стержня изменилась на 0,5%, то его длина теперь равна: L-0,005L=0,995L.
Из следствий теории относительности запишем формулу для изменения продольных размеров движущегося тела:
0,995L=L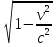 . .
Отсюда найдём скорость движения тела:
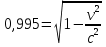 . .
Обе части возведём в квадрат, получим:
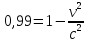 , отсюда найдём скорость: , отсюда найдём скорость:
V=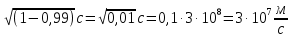
|
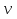 -? -?
|
Ответ: V= V=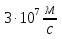
|
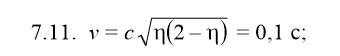 |
 Скачать 117.9 Kb.
Скачать 117.9 Kb.












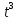 /32 рад Найти линейную скорость и ускорение точки, находящейся на расстоянии R= 0,8 м от оси вращения, в тот момент, когда её тангенциальное ускорение будет равно нормальному. Найти t1.
/32 рад Найти линейную скорость и ускорение точки, находящейся на расстоянии R= 0,8 м от оси вращения, в тот момент, когда её тангенциальное ускорение будет равно нормальному. Найти t1.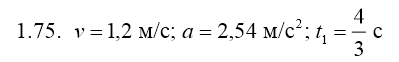

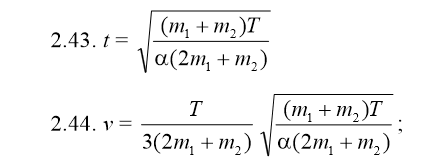


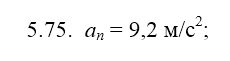
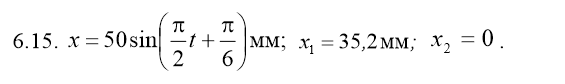
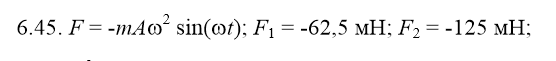
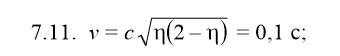

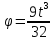
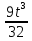 )/=
)/=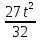
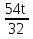
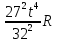
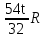
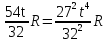
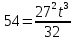 , t=
, t=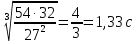
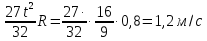
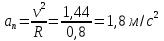
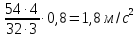
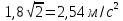
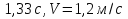 , а=
, а=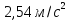
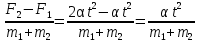
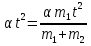 ,(
,( 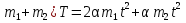
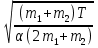
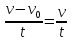
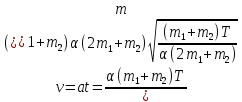
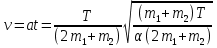
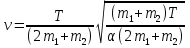
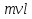 . Скорость пули найдём из формулы:
. Скорость пули найдём из формулы: 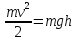 ,
, 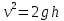 (1)
(1)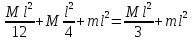 ,
, 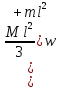 .
. 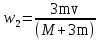
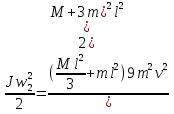 , учитывая (1), получаем:
, учитывая (1), получаем: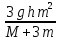
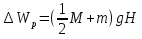 .
.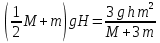
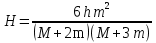
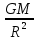 ,
, 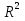 (1)
(1)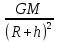 . (2)
. (2)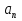 =
=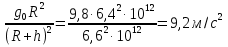 .
.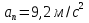
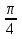
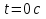
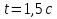
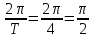 ;
; 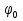 ).
).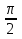 t+
t+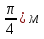 .
.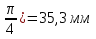
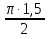 +
+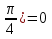
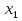 -?
-?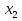 -?
-?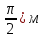 , Х1=
, Х1=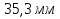 , Х2==0
, Х2==0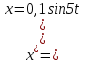
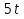 .
. 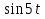
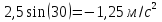
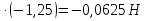 Н=-62,5мН
Н=-62,5мН