Основы электротехники 4 задача 7 вариант. 4задач7вар. Решение Определим входное сопротивление цепи относительно зажимов источника эдс r вх

• Название: Решение Определим входное сопротивление цепи относительно зажимов источника эдс r вх
• Анкор: Основы электротехники 4 задача 7 вариант
• Дата: 24.02.2022
• Размер: 217.21 Kb.
• Имя файла: 4задач7вар.docx
• Тип: Решение; #372154

КОНТРОЛЬНАЯ РАБОТА № 1

Задача 1

Ц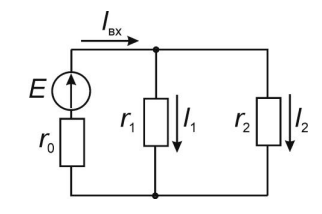
епь (Рис. 1) содержит источник напряжения с ЭДС Е и внутренним сопротивлением r₀. Сопротивления электроприемников равны r₁ и r₂. Определить токи в сопротивлениях r₁ и r₂, напряжение на зажимах электроприемников и составить уравнение баланса мощностей.

Рис. 1. Схема электрической цепи

Дано: r₁ = 13 Ом, r₂ = 10 Ом, E = 160 В, r₀ = 1.6 Ом.

Решение:

1. 
   Определим входное сопротивление цепи относительно зажимов источника ЭДС r_вх: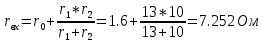
   

Далее, используя закон Ома, определим входной ток I_вх: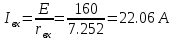



Напряжение U₁₂ на параллельном участке (r₁ и r₂) найдем, используя закон Ома: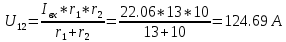



Токи в сопротивлениях r₁ и r₂ определим также, используя закон Ома: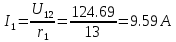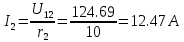

2. 
   Баланс мощностей: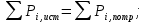
   

Мощность i – того источника ЭДС определяется как P_i,ист = E_i*I_i,

Мощность i – того потребителя (резистора) может быть рассчитана из соотношения: P_i,потр = R_i*I_i².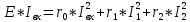



Подставляя в это уравнение рассчитанные токи ветвей, получим: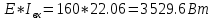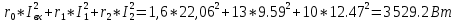





Следовательно, баланс мощности выполняется.

Задача 2

Д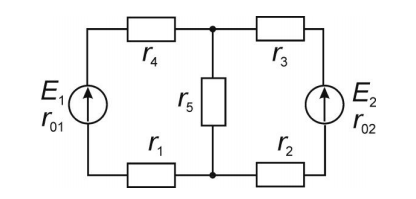
ля разветвленной электрической цепи постоянного тока (рис. 2.1), пользуясь законами Кирхгофа, определить токи во всех ветвях схемы.

Рис. 2.1 Схема разветвленной электрической цепи постоянного тока

Дано: Е₁ = 75 В, Е₂ = 90 В, r₀₁ = 0.18 Ом, r₀₂ = 0.3 Ом, r₁ = 9 Ом, r₂ = 8 Ом, r₃ = 40 Ом, r₄ = 18 Ом, r₅ = 9 Ом.

Решение:

Данная цепь содержит три ветви (в = 3), следовательно, необходимо определить три неизвестных тока. Как известно, число уравнений, составляемых по первому закону Кирхгофа, на единицу меньше, чем общее количество число узлов в схеме (у - 1). В рассматриваемом случае их два (у = 2). Следовательно, необходимо составить одно уравнение по первому закону Кирхгофа. По второму закону Кирхгофа составляют в – (у - 1) уравнений. В нашем случае по второму закону Кирхгофа необходимо составить два уравнения (3 – (2 - 1)). Выбирая условные положительные направления токов в ветвях цепи (рис. 2.2), направления обхода контуров и учитывая правила выбора знаков при записи уравнений по законам Кирхгофа, запишем: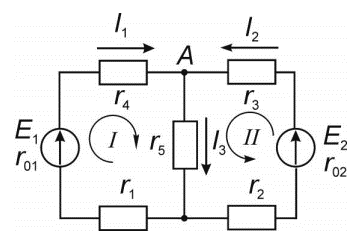



Рис. 2.2 Расчетная схема с выбранными направлениями токов ветвей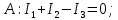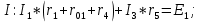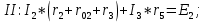







Решая полученную систему уравнений, находим значения токов ветвей I₁, I₂, I₃.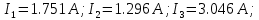



Задача 3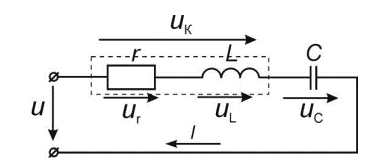

В цепь переменного тока напряжением U и частотой f = 50 Гц включены последовательно катушка с индуктивным сопротивлением xL и активным сопротивлением r и конденсатор емкостью C (Рис. 3.1). Пользуясь данными табл. 3, определить ток, а также, напряжение на зажимах катушки и конденсатора. Вычислить активную и реактивную мощности катушки, конденсатора и всей цепи. Определить, при какой частоте наступит резонанс и каковы при этом будут ток в цепи, напряжение на зажимах катушки и конденсатора, реактивные мощности катушки и конденсатора и активная мощность цепи. Для обоих случаев построить векторные диаграммы.

Рис. 3.1 Схема цепи переменного тока

Дано: U = 400 В, x_L = 50 Ом, r = 40 Ом, С = 500 мкФ.

Полное сопротивление цепи z, состоящей из последовательно соединенных катушки с индуктивным сопротивлением x_L и активным сопротивлением r и конденсатора емкостью C может быть записано в виде: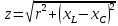



Здесь x_C – реактивное емкостное сопротивление: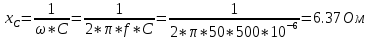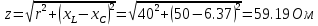





Ток цепи может быть определен на основании закона Ома: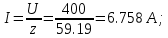



Для определения напряжения на зажимах катушки U_к найдем ее полное сопротивление z_k: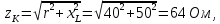



Напряжение на зажимах катушки Uк: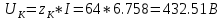



Напряжение на зажимах конденсатора U_С определяем по закону Ома: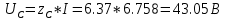



Активная мощность катушки P (это одновременно и активная мощность всей цепи):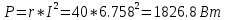



Реактивная мощность катушки Q_L: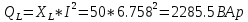



Реактивная мощность конденсатора Q_C: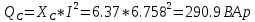



Полная мощность всей цепи S: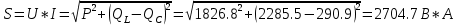



При последовательном соединении катушки и конденсатора возможно возникновение режима резонанса напряжений. Он наступает на частоте приложенного к цепи переменного напряжения, равной резонансной частоте последовательного контура ω₀: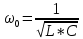



Индуктивность катушки определим из следующего соотношения: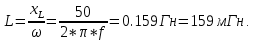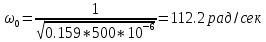





В режиме резонанса напряжений полное сопротивление цепи z₀ составит: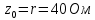



Ток цепи I₀ составит: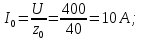



Полное сопротивление катушки на резонансной частоте z_К0: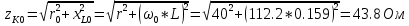



Напряжение на зажимах катушки U_к0 на резонансной частоте: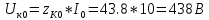



Напряжение на зажимах конденсатора U_С0 на резонансной частоте: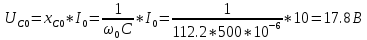



Реактивная мощность катушки Q_L0 на резонансной частоте: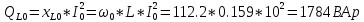



Реактивная мощность конденсатора Q_С0 на резонансной частоте: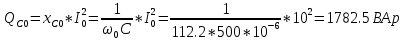



В режиме резонанса реактивная индуктивная мощность Q_L0 равна реактивной емкостной мощности Q_С0.

Активная мощность цепи P₀: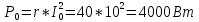



В режиме резонанса активная мощность цепи P₀ максимальна.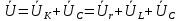



Здесь Ur – падение напряжения на активном сопротивлении катушки;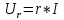



UL – падение напряжения на индуктивном сопротивлении катушки;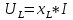



При построении топографической векторной диаграммы учтем, что фазовый сдвиг между напряжением и током составляет:

на резистивном элементе (R) - φ_R = 0°;

на индуктивном элементе (L) - φ_L = 90°;

на емкостном элементе (C) - φ_C = – 90°;

При построении вектор тока направим горизонтально и будем использовать в качестве базового при построении векторов напряжений (Рис. 3.2). Выберем масштаб по напряжению m_u = 20 В/см. Длины векторов напряжений определяются на основе рассчитанных ранее значений с учетом выбранного масштаба по напряжению.

Случай 1: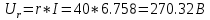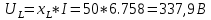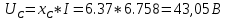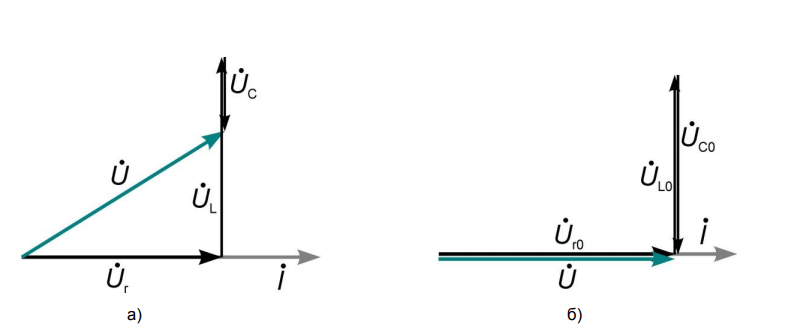







Случай 2 (резонансный режим):







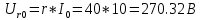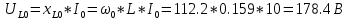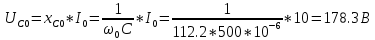Рис. 3.2 Векторные диаграммы для последовательной цепи переменного тока. а) Случай 1; б) Случай 2 (резонансный режим).

Задача 4

Для измерения мощности трехфазной цепи с симметричным линейным напряжением U_Л используются два ваттметра (Рис. 4.1, Табл. 4). Приемник содержит симметричные активно-индуктивные сопротивления z_ab = Z_bс = Z_са, соединенные треугольником. Мощность каждой фазы приемника равна Р_ф при коэффициенте мощности cosφ. Требуется: 1) построить векторную диаграмму цепи; 2) по данным диаграммы вычислить показания каждого ваттметра; 3) убедиться, что сумма показаний ваттметров равна активной мощности трехфазного приемника.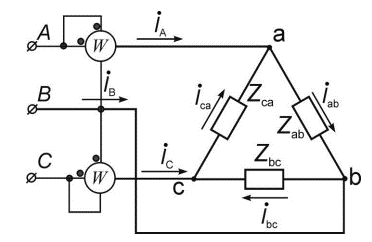



Рис. 4.1 Трехфазный потребитель, схема соединения - «треугольник».

Дано: U_Л = 380 В, P_ф = 7,6 кВт, cos φ = 0,8 Ом.

Решение:

При соединении фаз трехфазного потребителя по схеме «треугольник» фазные напряжения потребителя равны соответствующим линейным напряжениям: Uф = Uл. Для нахождения фазного тока воспользуемся известным значением активной мощности фазы: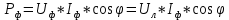

, отсюда фазный ток I_ф может быть рассчитан следующим образом: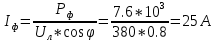



Фазные токи будут одинаковы во всех трех фазах трехфазного потребителя, так как потребитель, согласно условию задачи, является симметричным.

Для построения векторной диаграммы помимо величины фазного тока необходимо знать величину и знак угла фазового сдвига φ между фазным напряжением U_ф и фазным током I_ф. В таблице исходных данных к задаче приведен коэффициент мощности cosφ для каждого варианта, по которому определим угол сдвига фаз φ: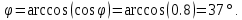



Указанный в задании активно-индуктивный характер сопротивления указывает на то, что фазное напряжение опережает фазный ток, а не наоборот !. Для нахождения линейных токов используют соотношения, которые могут быть получены на основе первого закона Кирхгофа: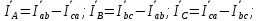



Все сказанное выше позволяет построить векторную диаграмму напряжений и токов. При построении учитывается 120° - сдвиг между фазными напряжениями трехфазного потребителя. Для нахождения показаний ваттметров на векторной диаграмме определяем (измеряем) углы φ₁ и φ₂. φ₁ – угол сдвига фаз между линейным напряжением U_AB и линейным током I_A, φ₂ – угол сдвига фаз между линейным напряжением U_СB и линейным током I_С. Обратим внимание, что линейное напряжение U_СB противоположно по направлению линейному напряжению U_BС, как это видно на векторной диаграмме. Величины линейных токов также измеряем на векторной диаграмме (Рис. 4.2). Показания ваттметров определяются из соотношений: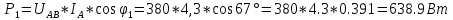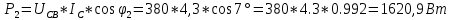





Активная мощность всего трехфазного потребителя P представляет собой сумму показаний обоих ваттметров: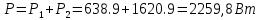



Учитывая симметричный характер сопротивлений трехфазного потребителя, активная мощность P может быть определена другими способами: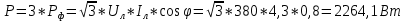



Баланс сошелся, неточность связана из-за погрешности измерения линейки и округления при подсчете.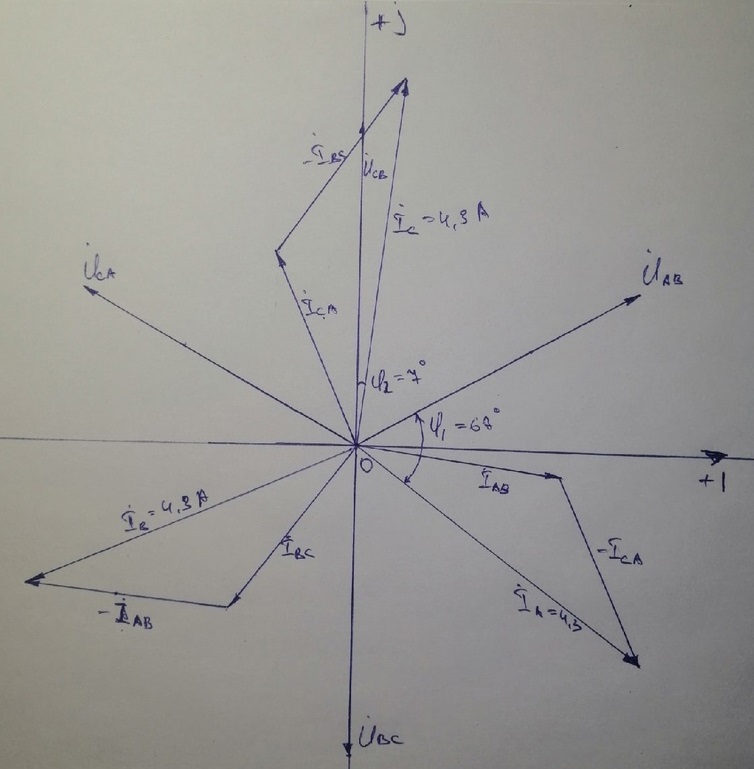



Рис. 4.2 Векторная диаграмма токов и напряжений