Курсовой проект Вариант 20. "Решение оптимизационных задач линейного программирования"

• Название: "Решение оптимизационных задач линейного программирования"
• Дата: 19.09.2022
• Размер: 481.41 Kb.
• Имя файла: Курсовой проект Вариант 20.docx
• Тип: Пояснительная записка; #684793
• страница: 3 из 3

5 Анализ базовой аналитической модели на чувствительность
В окончательной симплекс-таблице, содержащей оптимальное решение, содержится не только само оптимальное решение, но и другая информация. На основе последней симплекс-таблицы решаются задачи анализа на чувствительность – это анализ влияния изменений в постановке задачи (запасов ресурсов, величин прибыли от выпуска изделий и т.д.) на оптимальное решение. Во многих случаях анализ на чувствительность позволяет, не решая задачу заново, найти новое оптимальное решение задачи при изменениях в ее постановке.

Задачи линейного программирования, для решения которых применяются методы искусственного базиса, очень разнообразны по своему содержанию. Методы анализа на чувствительность, используемые для таких задач, и интерпретация результатов полностью зависят от постановки задачи.

5.1 Статус и ценность ресурсов
В рассматриваемой задаче ресурсом являются закупка материалов для производства конфет.

Как видно из остаточной переменной Х₅, которая равна нулю, это сырьё расходуется полностью. Увеличение этого ресурса позволит увеличить прибыль, а снижение приведёт к снижению прибыли.

Ценность ресурса представляет собой коэффициент Е-строки при остаточной переменной Х₅, соответствующей остатку ресурса (закупки сахарого песка), в симплекс таблице с оптимальным решением (Таблица 4). Значит ценность денежных средств, выделяемых предприятием на рекламу составляет 392,5 ден. ед. Это означает, что увеличение возможности закупки сахарного песка, приводит к увеличению прибыли предприятия в среднем на 392,5 ден.ед. Снижение выделяемых средств приведёт к соответствующему снижению прибыли.
5.2 Анализ на чувствительность к изменению количества ресурсов
Проанализируем, как влияют на оптимальный план производства изменения максимально возможной закупки сахарного песка. Пусть максимально возможное количество тонн закупки сахарного песка изменился на d тонн, т.е. составит не 800, а 800+d тонн. Для влияния изменения на оптимальное решение используются коэффициенты окончательной симплекс-таблицы (Таблица 4) из столбца переменной Х₅, так как эта переменная входит в изменившееся ограничение. Новое оптимальное решение определяется следующим образом:

Х₁=1000+1,25·d

Х₄=960+1,25·d (5.1)

Х₆=400−0,25·d

Х₇=120+0·d

Е=314000+392,5·d.
Пусть, например, можно закупать 850 тонн сахарного песка. Подставив в систему уравнений (5.1) d=50, получим оптимальное решение задачи:

Х₁=1000+1,25·50=1062,5

Х₄=960+1,25·50=1022,5

Х₆=400−0,25·50=300

Х₇=120+0·50=120

Е=314000+392,5·50=333625.
Таким образом, так максимально возможное количество закупки тонн сахарного песка, то новое оптимальное решение примет вид: Х₁=1062,5; Х₄=1022,5; Х₆=300; Х₇=120.

Определим диапазон изменения максимально возможной закупки сахарного песка, при котором состав переменных в оптимальном базисе остается прежним (т.е. базис оптимального решения будет состоять из переменных Х_3, Х_4, Х_6, Х₇). Для этого используем условие не отрицательности всех переменных:
Х₁=1000+1,25·d≥0

Х₄=960+1,25·d ≥0

Х₆=400−0,25·d≥0

Х₇=120+0·d≥0
Решая эти неравенства совместно, мы получаем: d≥-400 и 1600≥d.

Таким образом, базис оптимального решения будет состоять из переменных Х_3, Х_4, Х_6, Х_7, если максимально возможное количество закупки сахарного песка от 800-400 до 800+1600. Если же это ограничение выйдет из этого диапазона, то для получения нового оптимального решения необходимо будет перерешать задачу сначало.
5.3 Анализ на чувствительность к изменению коэффициента целевой функции
Выполним анализ на чувствительность к изменению затрат на производство конфет. Предположим, что прибыль от продажи конфет «Мечта» изменилась на d ден.ед. Для анализа влияния этих изменений на оптимальное решение используются коэффициенты окончательной симплекс-таблицы из строки переменной Х₁, так для этой переменной изменился коэффициент целевой функции. Новые значения коэффициентов Е строки при небазисных переменных (т.е. переменных Х₂, Х₃, Х₅) для окончательной симплекс-таблицы (Таблица 4), а так же новое оптимальное значение целевой функции определяется следующим образом:

Здесь F2, F₃, F₅ -новые значения коэффициентов Е-строки при небазисных переменных в окончательной симплекс таблице.

Пусть, например, прибыль от продажи конфет «Мечта» увеличился на 4 ден.ед. Найдем новые значения коэффициентов Е-строки при небазисных переменных для оптимальной симплекс-таблицы (Таблица 4) и новое оптимальное значения целевой функции. Решение будет следующим:

F₂=78,77

F₃= 110,5

F₅=400,5 (5.3)

Е=35400.

Новое оптимальное значение целевой функции Е=35400. Так как все коэффициенты Е-строки остаются не отрицательными, то оптимальное решение не изменяется.

Определим диапазон изменений затрат на производство деталей прямоугольного сечения, при котором останется оптимальным решение, найденное для исходной задачи. Условие оптимальности решения является не отрицательность всех коэффициентов Е-строки:

F₂=76,25+0,63d ≥0

F₃= 107,5+0,75d ≥0

F₅=395,5+1,25d ≥0 (5.3)

Решив эту систему неравенств, получим -_43,25 d. Это означает, что решение, найденное для исходной постановки задачи будет оптимально, если прибыль от продажи конфет «Мечта» составит не больше 270,75 ден.ед. Если же эта прибыль будет меньше, то для получения оптимального решения потребуется решить задачу заново, используя симплекс-метод. Новое оптимальное решение будет отличаться от начального не только значениями переменных, но и составом переменных в оптимальном базисе.
6 Построение модифицированной аналитической модели и анализ результатов модификации
Проанализировав результаты задачи оптимизации, можно сделать некоторые корректировке в системе производства:

Попробуем ввести в закупку сырья некоторые изменения. В нашем случае максимально возможное количество тон сахарного песка, которые можно закупить, составляют 800 тонн. Внесём в это условие небольшое изменение. Пусть это количество тон составит, допустим, 1000 тонн. Внесём изменения в ограничения и решим задачу заново. Решения будут следующие: Х1=1250; Х₂=0; Х₃=0; Х₄=1210; Х₅=0, Х6=350, Х7=120. Целевая функция увеличилась 392500 ден.ед. Следовательно, получается, что чем больше мы сможем закупать сахарного песка, тем больше мы сможем производить карамель «Мечта» и получать прибыль.

Проверку результатов модификации выполним с помощью Simplex-M. Результаты проверки приведены в Приложениях В.

7 Примеры постановок и решение оптимизационных задач
Пример 1.

Денежные средства в размере 200 млн ден.ед. следует вложить в четыре крупнейших банка страны ( все или какую-то их часть). Характеристики процентных ставок этих банков приведены в таблице.

Объект	Процентная ставка, %	Срок, годы	Рейтинг, баллы
№1	10	2	5
№2	9	3	2
№3	8	3	5
№4	11	1	3

Это означает, например, что денежные средства, вложенные в банк №1, будут приносить прибыль, которая составит 10% от вложенной суммы каждый год, т.е. после первого года сумма изменится и будет составлять 1,1 от вложенных денежных средств, следовательно, прибыль полученная после истечения второго года вклада составит 0,1*1,1=0,11, а вся сумма 1,1+0,11=1,21 от вложенных вначале денежных средств, т.е. прибыль за 2 года составит 0,21 от вложенных средств. Вложение средств в банк №1 достаточно престижно и надежно (рейтинг составляет пять баллов).

Существуют определенные требования к тому, каким образом должны быть распределены денежные средства: 1) максимально возможная сумма, вложенная в каждый банк, может составлять 50% от всех предложенных денежных средств; 2) необходимо, чтобы как минимум половина всех средств были вложены на 3 года или более длительный период; 3) в банки, рейтинг которых составляет менее 5 баллов, можно вложить не более одной четверти всех предложенных денежных средств.

Составить план вложения денежных средств, обеспечивающий получение максимальной прибыли.
Составим ограничения на содержание удобрений:

15X1 + 5X2 + 25X3 ≥ 40,

5X1 + 10X2 + 20X3 ≥ 15.

Ограничение, указывающее, что сумма долей удобрений в подкормке должна быть равна 1:

X1 + X2 + X3 = 1.

По физическому смыслу все переменные в этой задаче должны быть неотрицательные:

Xi ≥ 0, i= 1…3.

Целевая функция (стоимость подкормки) будет иметь вид:

Е = 110X1+ 90X2 + 75X3 → min.
Приведём математическую модель в целом:
15X1 + 5X2 + 25X3 ≥ 40,

5X1 + 10X2 + 20X3 ≥ 15,

X1 + X2 + X3 = 1,

Xi ≥ 0, i= 1…3,

Е = 110X1+ 90X2 + 75X3 → min.
Решив задачу симплекс-методом, подробное решение приведено в “Приложении Д”, получим: X1= 0, X2= 0, X3= 1, E= 75. Это значит, что подкормка должна состоять полностью из удобрения Т3, удобрения Т1 и Т2 использовать нецелесообразно. Стоимость одного килограмма подкормки будет 75 д.е.. Очевидно, что в подкормке будет содержаться 25 % азотных добавок и 20 % фосфатов.

Пример 2.

Руководство нового развивающегося коммерческого предприятия А на прошлой неделе заключило три очень выгодных контракта, вложив в сумме 100 млн. ден. ед. Характеристики и все основные данные о прошедших сделках описаны в таблице:

Объект	Предполагаемая прибыль, %	Срок, годы
Контракт №1	10	2
Контракт №2	9	3
Контракт №3	8	3

Это означает, например, что денежные средства, задействованные по первому контракту, через два года принесут прибыль в размере 10% от вложенных средств.

При заключении данных сделок, руководство предприятия А предъявляло определенные требования: 1) доля средств, задействованных по какому-либо одному из контрактов, не может превышать 50% от имеющихся средств; 2) более половины всех средств должны представлять собой долгосрочные инвестиции со сроком получения дохода не менее трех лет. Существует еще одно очень важное условие: чтобы погасить все кредиты в срок, прибыль предприятия А должна составить не менее 10 млн ден. ед.

Несколько дней назад, руководству было предложено заключить еще один контракт сроком на 2,5 года.

Итак, найти какую минимальную прибыль (в процентах) должны предложить руководству компании А, чтобы оно согласилось заключить четвертый контракт и составить план распределение денежных средств.
Введём переменные:

X1 – количество машин стоимостью 6 тыс.р.,

X2 – количество машин стоимостью 3 тыс.р.,

X3 – количество машин стоимостью 2 тыс.р..
Составим ограничение на стоимость машин:

6X1 + 3X2 + 2X3 ≤ 300,

общая стоимость оборудования не должна превышать 300 тыс.р.
Данное оборудование должно быть размещено на территории не более 45 кв.м:

9X1 + 4X2 + 3X3 ≤ 45.
Количество машин стоимостью 6 тыс.р. должно быть не менее 2:

X2 ≥ 3.
По физическому смыслу все переменные в этой задаче должны быть неотрицательные:

Xi ≥ 0, i= 1…3.
Целевая функция (производительность всего участка) будет иметь вид:

Е = 8X1+ 4X2 + 3X3 → max.
Приведём математическую модель в целом:

6X1 + 3X2 + 2X3 ≤ 300,

9X1 + 4X2 + 3X3 ≤ 45,

X2 ≥ 3,

Xi ≥ 0, i= 1…3,

Е = 8X1+ 4X2 + 3X3 → max.
Решив задачу симплекс-методом, подробное решение приведено в “Приложении Е”, получим: X1= 0, X2= 3, X3= 11, E= 45. Это значит, что необходимо приобрести 3 машины за 3 тыс. р., 11 машин за 2 тыс. р., закупать машины за 6 тыс. р. нецелесообразно. Производительность всего участка составит 45 тыс..

Заключение
После решения данной задаче, мы видим, что для того чтобы иметь наибольшую прибыль предприятию достаточно производить карамель «Мечта». Так же определили, что с увеличением возможности закупки сахарного песка, у предприятия будет увеличиваться прибыль. Остальные же материалы для производства конфет можно не изменять. Так как из решения видно, что остаточные переменные не равны нулю. Максимальная прибыль при такой задаче составляет 314000 ден.ед. после того как мы модифицировали условие задачи, видно, что прибыль увеличилась. Значить их производить целесообразно.

Список используемой литературы

1. 
   Математический практикум А.Г.Трифонов. "Постановка задачи оптимизации и численные методы ее решения" - http://matlab.exponenta.ru/optimiz/book_2/1.php.
   

2. 
   Системный анализ и исследование операций. Сборник заданий и методические указания по курсовому проектированию для студентов специальности I – 530102./ C.С. Смородинский, Н.В. Батин. – Мн.: БГУИР, 2006. – 72с.
   

3. 
   Оптимизация решений на основе методов и моделей математического программирования: Учебное пособие по курсу спец. “Системный анализ и исследование операций” дневн. и дистанц. форм обучения/ C.С. Смородинский, Н.В. Батин. – Мн.: БГУИР, 2003. – 136 с.
   

4. 
   Исследование операций / Википедия – свободная энциклопедия, 2007 — http://ru.wikipedia.org/wiki/Исследование_операций.
   

5. 
   Исследование операций. Для продвинутых математиков. Кононов В.А. 113 с. -http://allmath.ru/appliedmath/operations/operations25/operations.htm.-
   

6. 
   Вентцель Е.С. Исследование операций. Задачи, принципы, методология. - М.: Наука, 1980.-208.-библ.: 31.
   

7. 
   Автоматизированные системы управления / примеры задач на оптимизацию - http://www.asu.ru/files/math/2_uprajneniya.html#013.
   

Приложение А

(Справочное)
Решение базовой задачи на программе Simplex-M.
ТаблицаА.1.

ТаблицаА.2.

Таблица В.3.


ТаблицаА.4.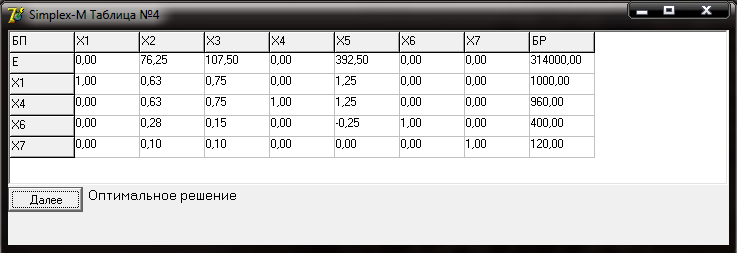

Решение:


Приложение Б

(Справочное)
Решение базовой задачи при помощи Excel.
Таблица Б.1.


Приложение В

(Справочное)
Решение модифицированной задачи 1 (введение дополнительной мельницы) на программе Simplex-M.

Таблица В.1.

Таблица В.2.


Таблица В.3.

Таблица В.4.

Решение:

Приложение Г

(Справочное)
Решение примера 1 на программе Simplex-M.
Таблица Г.1.

Таблица Г.2.

Таблица Г.3.


Таблица Г.4.

Таблица Г.5.

Таблица Г.6.


Таблица Г.7.

Таблица Г.8.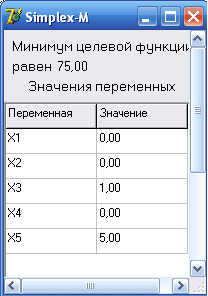



Приложение Д

(Справочное)
Решение примера 2 на программе Simplex-M.
Таблица Д.1.


Таблица Д.2.


Таблица Д.3.



Таблица Д.4.


Таблица Д.5.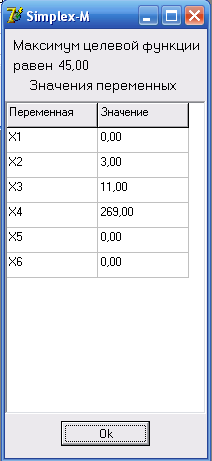