Контрольная работа_11.09_Ебург_ВК_УрГЭУ_Вариант 6. Решение опвп 500 100 580 86,2 Таким образом, выпуск компьютеров в декабре составил 86,2 запланированного выпуска
 Скачать 261.5 Kb. Скачать 261.5 Kb.
|
|
Содержание Задание 1 3 Задание 2 4 Задание 3 5 Задание 4 6 Задание 5 7 Задание 6 8 Задание 7 9 Задание 8 10 Задание 9 Основные направления использования средних величин и показателей вариации в социально-экономических исследованиях (за последние 5 лет) 11 Список источников и литературы 16 Задание 1Определить относительный показатель выполнения планового задания ОПВП фирмы, если в декабре был поставлен план выпустить 580 тыс. компьютеров, а было выпущено 500 тыс. компьютеров. Решение ОПВП = 500 *100/ 580 = 86,2% Таким образом, выпуск компьютеров в декабре составил 86,2 % запланированного выпуска. Задание 2Бригада операторов компьютерного набора из 3 человек выполняет набор книги в 500 страниц. Первый оператор тратит на набор 1 страницы 15 мин., второй - 20 мин., и третий - 30 мин. Сколько времени в среднем требуется операторам на набор одной страницы? Решение 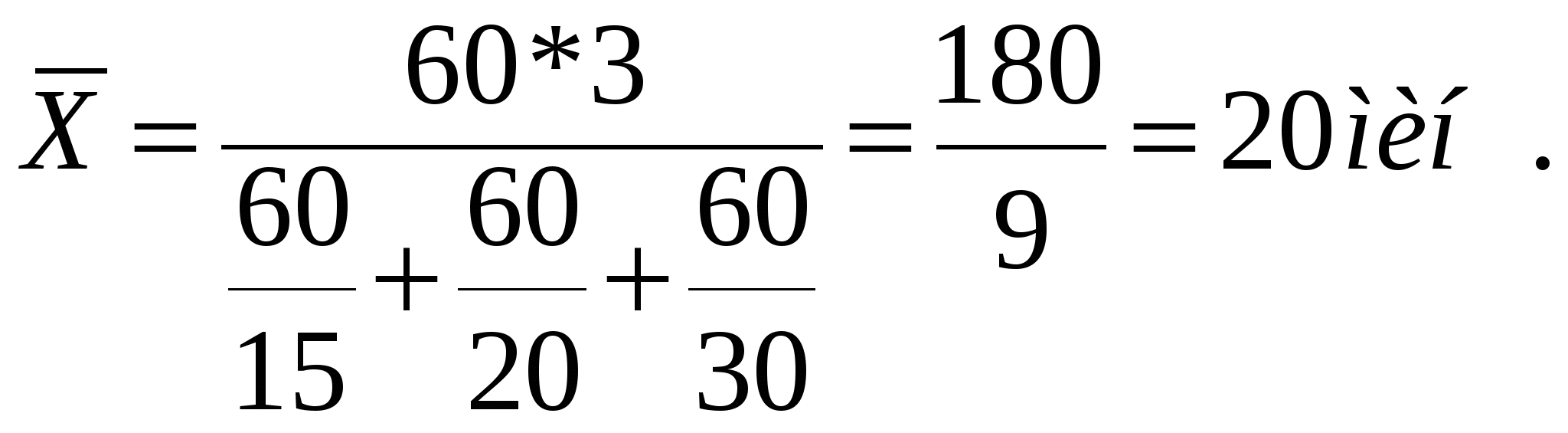 Задание 3Средняя величина признака равна 40, а коэффициент вариации - 15%. Рассчитайте дисперсию признака, дайте характеристику понятия общая дисперсия. Решение Коэффициент вариации определяется Отсюда определим дисперсию Дисперсия означает, что средний квадрат отклонений индивидуальных значений признака от их средней величины (равной 40) составляет 0,245. Задание 4Из партии готовой продукции методом случайного бесповторного отбора отобрано 250 изделий, из которых 50 оказались бракованными. Определить с вероятностью 0,954 возможные пределы процента брака во всей партии. Объем выборки составляет 10% от всего объема готовой продукции Решение Возможные пределы процента брака во всей партии, определяется: где При Р=0,954 t=2 Выборочная доля - это удельный вес единиц с определенным признаком (m) в выборке (n): Число бракованных изделий равно 50. W = 50 / 250 = 0,20 Так как выборка 10%-ая N = n/0,10 = 250 / 0,10 = 2500 изделий Возможные пределы процента брака во всей партии равны Таким образом, процент брака во всей партии будет составлять от 0,152 до 0,248 или от 15,2% до 24,8%. Задание 5Рассчитать средний остаток оборотных средств (с точностью до 0,1 млн руб.) за второй квартал, при условии
Решение Средний остаток оборотных средств равен: 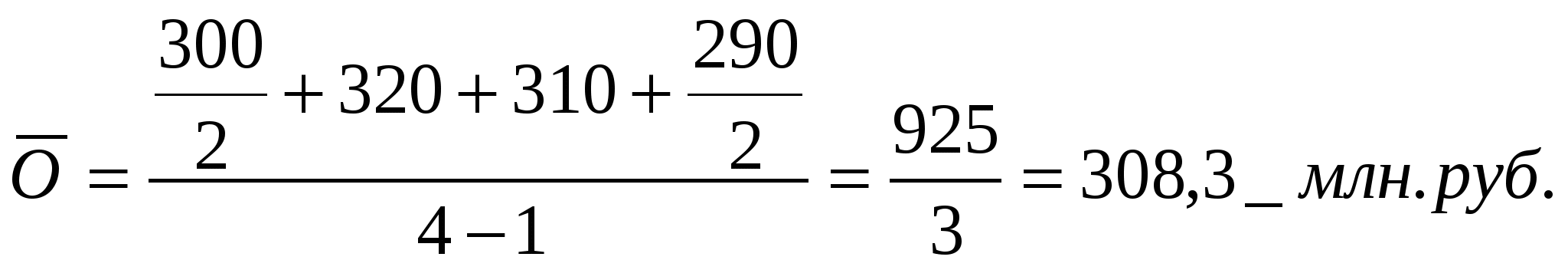 Средний остаток оборотных средств за второй квартал составил 308,3 млн.руб. Задание 6Найти величину индекса средних цен переменного состава при условии, что индекс средних цен постоянного состава 105,4%, а индекс структурных сдвигов 95,2%. Решение Используем взаимосвязь индексов Индекс средних цен переменного состава равен 100,3%. Задание 7Определить численность активного населения по следующим данным: численность занятых в материальном производстве 1000 тыс. чел.; занятых в сфере услуг 500 тыс. чел.; численность официально зарегистрированных безработных 100 тыс. чел.; общая численность трудоспособных лиц в рабочем возрасте, ищущих работу 50 тыс. чел. Решение ЭА = З + Б, где З – занятые; Б – безработные. З = 1000 + 500 = 1500 тыс.чел. Б = 100 + 50 = 150 тыс.чел. ЭА = 1500 + 150 = 1650 тыс.чел. Таким образом, численность активного населения составляет 1650 тыс.чел. Задание 8Известны следующие данные: среднесписочная численность работников предприятия составляла в феврале 310 чел., в марте 320чел. (предприятие начало работать с 10 февраля). Определить среднесписочную численность предприятия в I квартале. Решение Среднесписочная численность предприятия в I квартале составила 210 человек. Задание 9 Основные направления использования средних величин и показателей вариации в социально-экономических исследованиях (за последние 5 лет)Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом или анализом различных по виду и форме выражения статистических показателей. Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Качественная определённость показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью. 7, с. 76 Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина. Средняя величина – обобщающая числовая характеристика изучаемого количественного признака по всем единицам статистической совокупности. Отличительной чертой средних величин является то, что в них взаимно погашаются индивидуальные различия признака. Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака. Известно, что единицы каждого массового явления обладают многочисленными признаками. Какой бы из этих признаков мы ни взяли, его значения у отдельных единиц будут различными, они изменяются, или, как говорят в статистике, варьируют от одной единицы к другой. Так, например, заработная плата работника определяется его квалификацией, характером труда, стажем работы и целым рядом других факторов, поэтому изменяется в весьма широких пределах. Совокупное влияние всех факторов определяет размер заработка каждого работника, тем не менее можно говорить о среднемесячной заработной плате работников разных отраслей экономики. Здесь мы оперируем типичным, характерным значением варьирующего признака, отнесенным к единице многочисленной совокупности. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что характерно для всех единиц изучаемой совокупности. В то же время она уравновешивает влияние всех факторов, действующих на величину признака отдельных единиц совокупности, как бы взаимно погашая их. Уровень (или размер) любого общественного явления обусловлен действием двух групп факторов. Одни из них являются общими и главными, постоянно действующими, тесно связанными с природой изучаемого явления или процесса, и формируют то типичное для всех единиц изучаемой совокупности, которое и отражается в средней величине. Другие являются индивидуальными, их действие выражено слабее и носит эпизодический, случайный характер. Они действуют в обратном направлении, обусловливают различия между количественными признаками отдельных единиц совокупности, стремясь изменить постоянную величину изучаемых признаков. Действие индивидуальных признаков погашается в средней величине. В совокупном влиянии типичных и индивидуальных факторов, которое уравновешивается и взаимно погашается в обобщающих характеристиках, проявляется в общем виде известный из математической статистики фундаментальный закон больших чисел. 5 В зависимости от характера изучаемых явлений, конкретных задач и целей статистического исследования могут применяться различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя хронологическая и структурные средние (мода, медиана). Выбор вида средних зависит от исходных данных и содержания определяемого показателя. Вариация - это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию. Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей. Существует определенная статистика, которая указывает, в каком году был среднемесячный и среднегодовой заработок россиянина в национальной и иностранной наиболее ходовой валюте. Такие статистические данные нужны для того, чтобы отслеживать рост экономики страны, динамику развития. Существуют данные о средней зарплате в России по годам, начиная со времен Советского Союза, и заканчивая текущим годом. Подобная статистика интересна, в первую очередь, историкам, занимающимся изучением хронологических аспектов из области экономики, самим экономистам и потенциальным мигрантам, которые собираются зарабатывать в будущем в РФ. Для изучения данного вопроса детально, следует поинтересоваться исторической статистикой по зарплатам за последние десятилетия и прошлые столетия. А также такие данные помогут работникам приблизительно рассчитать пенсионные начисления для Пенсионного Фонда. Существуют расчетные схемы, по которым можно узнать свою прибыль по начислениям в будущем. Чтобы правильно вычислить коэффициент среднего показателя дохода за месяц, нужно рассчитать соотношение оплаты за какой-то конкретный промежуток времени, к примеру, за 2016 и 2017 год или последние 5 лет до 1 января 2017 года, к средней месячной оплате труда в России за выбранный отрезок по годам. Из вышесказанного становится понятно, что коэффициент средней оплаты труда за 30 дней равняется заработной плате человека, разделенной на среднестатистическую зарплату в месяц. Формула: КСЗ=ЗР/ЗП. Полученная цифра используется для вычисления расчётной пенсии, часть суммы от будущих выплат, которые заработаны за весь 2017 год. Средняя зарплата в России в рублях, 1999-2017, инфографика 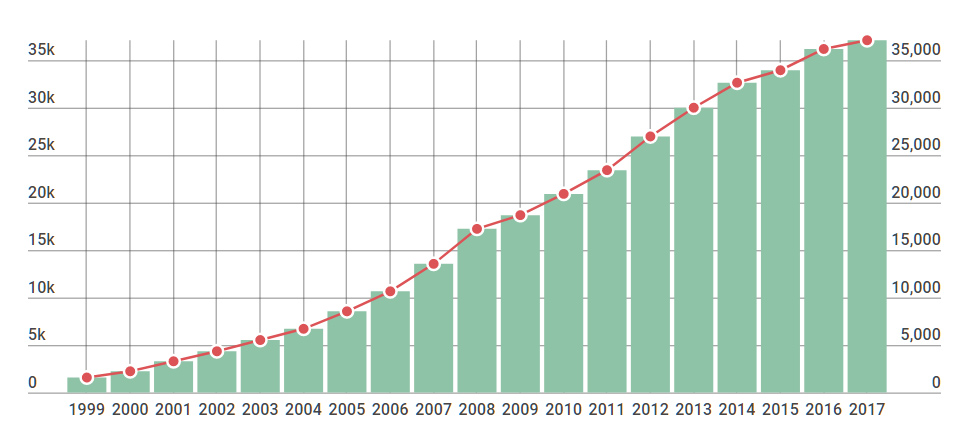 Таблица 1 - Средняя зарплата в России в рублях, 1999-2017
Рост номинальной средней заработной платы в рублях с 1999 года выглядит впечатляющим - с 1,5 до 37 тысяч рублей. Однако, если мы вспомним об инфляции, то поймем, что ориентироваться на рублевые показатели не совсем корректно. Инфляция за это время в сумме составила 230%. Долларовый эквивалент российской зарплаты уже выглядит не так радужно, что мы фактически и ощущаем на своем кармане. Таблица 2
Достигшая своего максимума в $915 в 2013 году зарплата, упала почти на половину в 2014-2015 и понемногу стала восстанавливаться в 2016-2017 гг., достигнув уровня 2009 года. В нынешних реалиях это 69-е место в мире. Вернуться к значениям 2013 года, по оптимистичным прогнозам Минэкономразвития средняя зарплата россиянина сможет не раньше, чем через 20 лет. При этом такую цифру призван обеспечить рост ВВП на более чем 3% в год, что пока представляется маловероятным: за последние 6 лет ВВП вырос на 0,3%. Список источников и литературы
|
