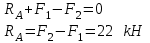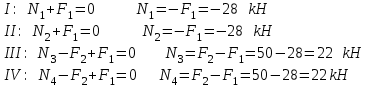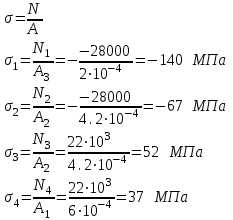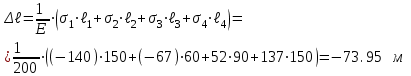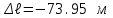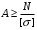ргр. Решение Освободимся от связей и рассчитаем значение реакции r a
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
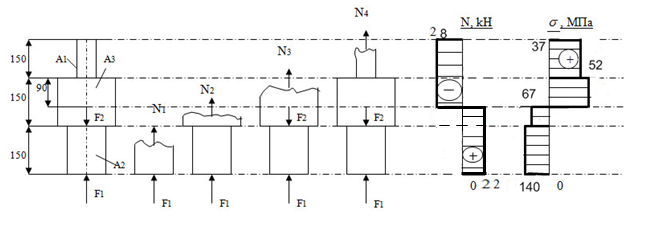
Задача 19.Трехступенчатый стальной брус нагружен силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение бруса, приняв Е=2·105 МН/м2. 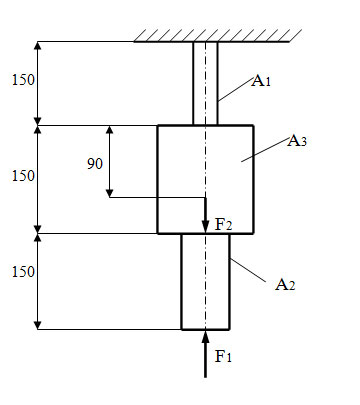

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дано: F1 = 18 кН F2 = 18 кН F3= 46 кН [σр]=50 Н/мм2 [σс]=120 Н/мм2 | |
| А- ? | |
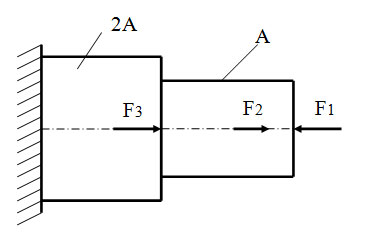

Решение
Брус разбивается на пять участков (в местах приложения сил и местах изменения площади сечения).
На каждом из участков проведем сечения 1, 2, 3, 4, 5. Будем последовательно рассматривать сечения, мысленно отбрасывая левые их части.
3
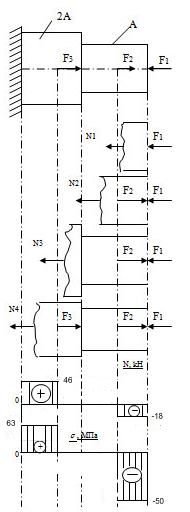
Исходя из уравнений равновесия для каждого сечения, найдем усилия
N
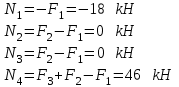
1, N2, N3, N4:
Строим эпюру поперечных усилий.
Теперь, зная у
 силия, возникающие в сечениях, можем определить напряжения σ1,σ2,σ3,σ4 в брусе. Т.к. усилия в нем положительны - брус сжат.
силия, возникающие в сечениях, можем определить напряжения σ1,σ2,σ3,σ4 в брусе. Т.к. усилия в нем положительны - брус сжат.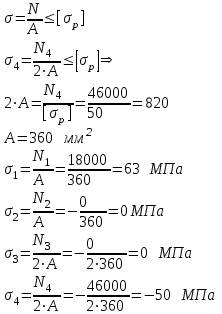
Ответ: A=360
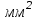
4
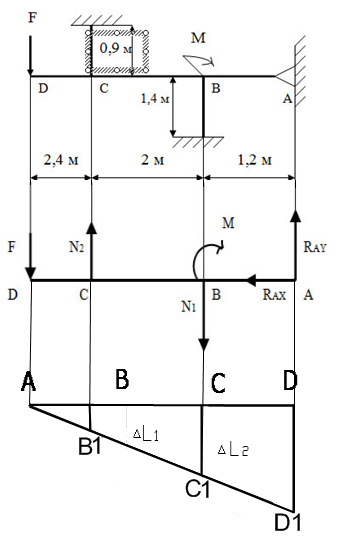
Задача 21. Определить требуемый размер поперечного сечения стальных стержней, удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом, если [σ]=160 МПа. Определить требуемое значение площади А, найти напряжения в поперечных сечениях обоих стержней.
| Дано: F = 19 кН M=30 Н∙м A1=A2 | |
| А- ? | |

Решение
Освобождаемся от связей. Изображаем реакции. Обозначаем характерные точки. Выбираем систему координат.
Составим уравнения равновесия для заданной системы сил:
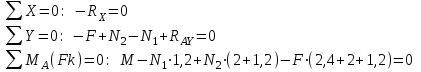
Три неизвестные, два уравнения. Задача статически неопределима. Запишем уравнение перемещений, проиллюстрировав его соответствующей схемой.
Из подобия треугольников и имеем:
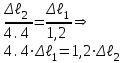
По формуле Гука:
5
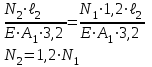
Вернемся к уравнениям равновесия, записанным выше
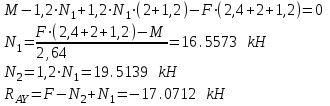
Для определения площади поперечного сечения воспользуемся проектным расчетом:
Максимальное уси
 лие, которое необходимо использовать в этой формуле в нашем случае равно N2.
лие, которое необходимо использовать в этой формуле в нашем случае равно N2.Подставим значения
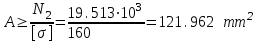
Ответ:
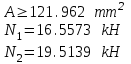
6

Задача 22. Биметаллический провод провод подвешивается на горизонтальном пролете l. Требуется определить:
Стрелу провисания f1 в летних условиях с тем, чтобы в зимних условиях напряжение в проводе не превысило допускаемое.
Распределение усилий и напряжений по различным материалам биметаллического провода в летних и зимних условиях.
«Тяжение» провода в летних и зимних условиях N1 и N2.
Дать заключение о запасе прочности в различных частях провода.
Решение.
1. Составляем таблицы механических характеристик составных частей провода и исходных данных.
Механические характеристики составных частей провода
| Модуль упругости, Н/мм2 | Коэффициент расширения, 1/град | Предел прочности, Н/мм2 (МПа) | Удельные веса, Н/см3 = Н/ммм2 | |||||||
| ЕА | ЕС | А | С | 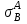 | 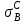 | А | С | |||
| 7104 | 21104 | 2510-6 | 12,510-6 | 200 | 800 | 2710-3 | 7810-3 | |||
Исходные данные
| Сечение | Длина | Температура | Отношение площадей | Отношение нагрузки | Запас прочности | Площади сечений | ||
| А, мм2 | l, м | t1 | t2 | АА/AC | k1 = 2/1 | [S] | АА | АC |
| 360 | 375 | 18 | -16 | 9,0 | 2.5 | 2,7 | 324 | 36 |
2. Определяем приведенные величины биметаллического провода по формулам. Причем для ускорения вычислений эти формулы следует упростить, разделив числители и знаменатели некоторых формул на АС, а одну из формул – на произведение ЕСАС и вводя при этом коэффициенты

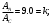
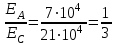 .
.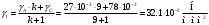 ;
;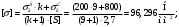 ;
;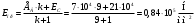 ;
;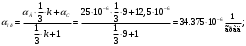
3. По результатам приведенных величин и формулам последовательно получаем вспомогательные коэффициенты:
2 = k11 = 2.5 32.1 10-3 = 80.2510-3
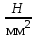 ;
;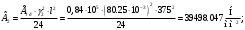
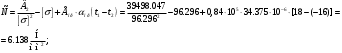
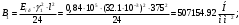
4. По результатам расчетов приведенных величин составляем табл.
Приведенные величины
| Епр, МПа | 1, Н/ммм2 | [], МПа | пр, град-1 | B1, МПа | С, МПа |
| 0,84105 | 32.110-3 | 96.296 | 34.37510-6 | 50.71104 | 6.138 |
Найденные числа позволяют составить «уравнение состояния провода»:
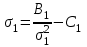 ;
;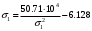 .
.5. Решаем уравнение методом подбора. Окончательно 1 = 51.75 МПа.
6. Определяем и анализируем результаты расчетов, сведенные в табл..
Необходимая стрела провисания:

летом
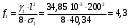 м;
м;зимой
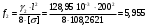 м.
м.Близость результатов указывает на то, что зимняя нагрузка 2 скомпенсировала температурное укорочение провода.
Летнее и зимнее «тяжение» провода:
N1 = 1(AA + AC) = 40,34(460) = 18556 Н;
N2 = [](AA + AC) = 108,2621(460) = 49801 Н.
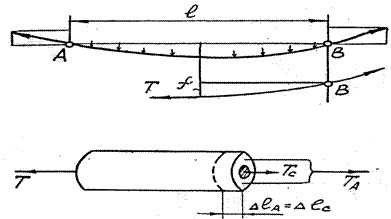
Очень важно вычислить и осмыслить распределение растягивающего усилия N1 и N2 по материалам провода, т. е. в алюминиевой NА и стальной NС частях.
Из соотношения
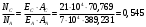
найдем NС и NА в летний и зимний периоды:
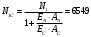 Н;
Н; 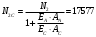 Н.
Н.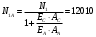 Н;
Н; 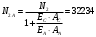 Н.
Н.Усилия в алюминии и стали распределяются прямо пропорционально «жесткостям сечений», то есть произведениям площадей на модули упругости.
Выясняется, что растягивающие напряжения оказываются пропорциональными модулям упругости материалов независимо от площадей. Определим напряжения в частях биметаллического провода:
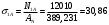 МПа;
МПа; 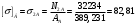 МПа.
МПа.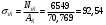 МПа;
МПа; 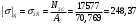 МПа.
МПа.
Оценка прочности частей биметаллического провода:
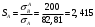 ;
;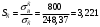 .
.Результаты расчетов
| 1, МПа | f1, м | N1, Н | [], МПа | f2, м | N2, H | N2A, H | N2C, H | 2C, МПа | 2A, МПа | SC | SA |
| 40,34 | 4,3 | 18556 | 108,2621 | 5,955 | 49801 | 32234 | 17577 | 248,37 | 82,81 | 3,221 | 2,415 |
Вывод: т.к. SC>[S], а SA<[S], то это значит, что прочностных характеристик стали достаточно, а алюминия – не достаточно.
Задача 23. Для заданной консольной балки построить эпюры поперечных сил и зигибающих моментов и подобрать размеры поперечного сечения в двух вариантах ( двутавр или прямоугольник с заданным отношением h/b высоты и ширины).
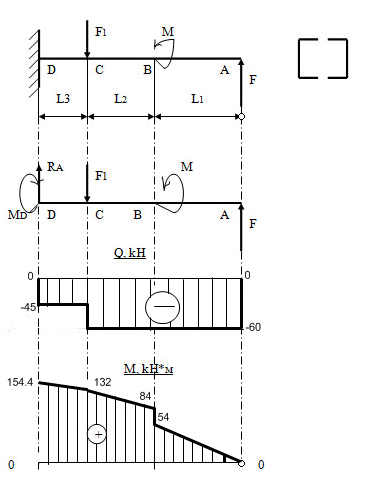
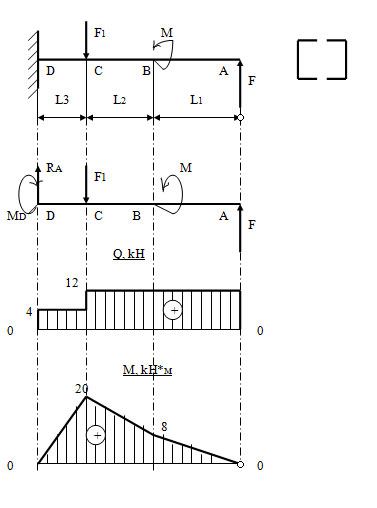
| Дано: F = 60 кН F1=15 кН М = 30кН·м [σ]=160 МПа h/b=3 l1=0.9 l2=0.8 l3=0,5 | |
| Cечение, эпюры ? | |

Решение
Освобождаемся от связей, обозначая реакции. В точке D—глухая заделка, поэтому кроме реакции RD, направленной вертикально, здесь будет еще и момент МD.
Из уравнений равновесия определим реакции:
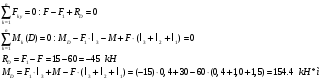
12
 Зная реакции, можно определить поперечные силы в балке
Зная реакции, можно определить поперечные силы в балке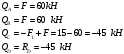
Строим эпюру поперечных напряжений.
Определим изгибающие моменты в характерных точках
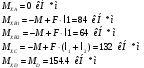
Строим эпюру изгибающих моментов.
Для того, чтобы подобрать размеры поперечного сечения, запишем условие прочности:
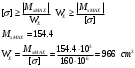
Рассмотрим случай швеллера:
По табл. находим ближайшее большее значение WX=13,5 см2, которому соответствует балка № 12П.
Рассмотрим случай прямоугольника:
WX в этом случае вычисляется по формуле:
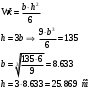
Ответ: h=25.869 cм b=8.633 см
Балка № 33
 Задача 24. Для заданной двухопорной балки построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения(круг или квадрат). Для материала балки (сталь Ст3) с учетом повышенных требований к её жесткости принять[σ]=130 МПа.
Задача 24. Для заданной двухопорной балки построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения(круг или квадрат). Для материала балки (сталь Ст3) с учетом повышенных требований к её жесткости принять[σ]=130 МПа. 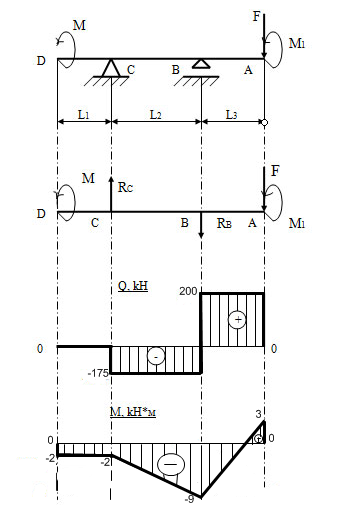
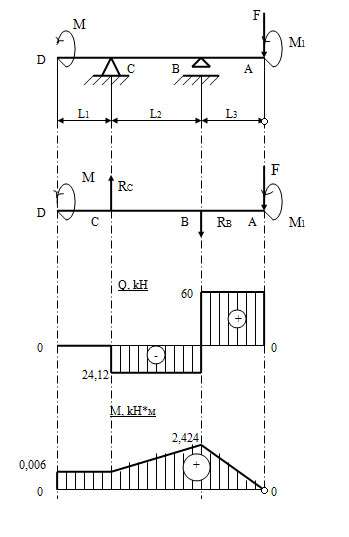
| Дано: F=200 кН M1=3 Н∙м L1=30 мм L2=60 мм L3=60 мм M=2 Н∙м Сечение - круг |
| а - ? |

Решение
Сперва найдем реакции RB и RC. Для этого запишем уравнения моментов относительно точек B и C.
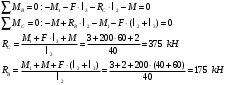
14
Проверка:
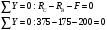
Построим эпюру поперечных усилий Q. Для это найдем поперечные усилия в критических точках A,C,D,B с учетом правила знаков.
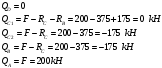
Построим эпюру изгибающих моментов Мх
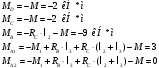
В данной задаче нам необходимо произвести проектный расчет для нахождения диаметра сечения бруса
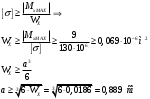
Ответ:
13

Задача 25. Для заданной балки определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и из условия прочности балки на изгиб определить допускаемую нагрузку, если [σ] = 100 МПа.
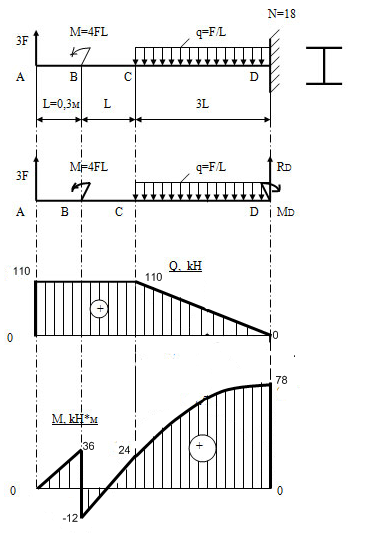
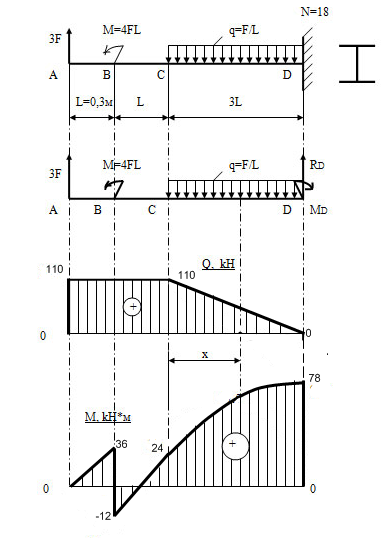
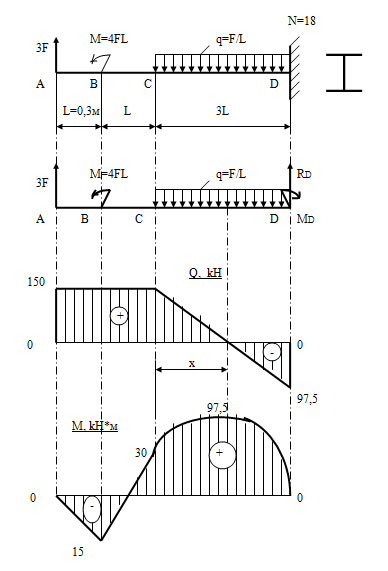
| Дано: F = 40 кН | |
| RA , RC – ? | |

Решение
Сначала вычислим нагрузку:
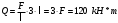
Для нахождения реакций составим уравнения равновесия:
16
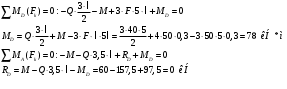
Выполним проверку
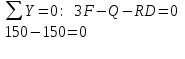
Определим усилия, возникающие в поперечных сечениях балки:
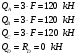
Определим изгибающие моменты в характерных точках:
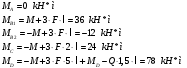
По табл. берем Wx , затем определяем допускаемую нагрузку
17

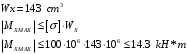
Ответ:
Задача 27. Для стального вала постоянного поперечного сечения с двумя зубчатым колесами, передающего мощность P при угловой скорости , рад/с: а) определить вертикальные и горизонтальные составляющие реакций подшипников; б) построить эпюру крутящих моментов; в) построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях; г) определить диаметр d вала, приняв [] = 70 Н/мм2 и полагая Fr1 = 0,36Ft1; Fr2 = 0,36Ft2.
| Дано: P = 30 кВт ω=48 рад/c σ=60 H/мм2 | |
| RB , RD – ? D - ? | |
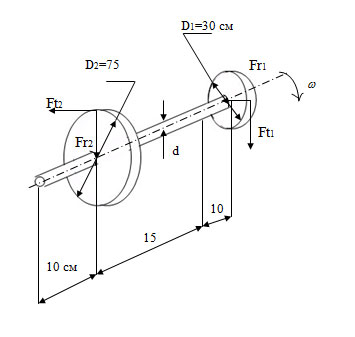
Решение
Для удобства вычислений перейдем в другую изометрию.
Определим Т:
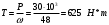
Окружные силы:
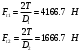

19
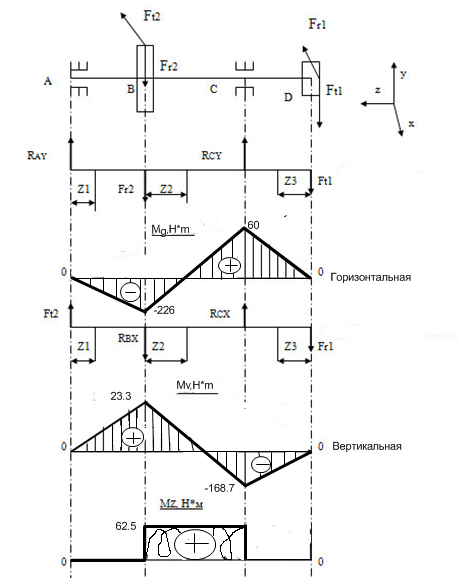

20
Радиальные силы:
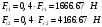
Составляем расчетную схему вала в вертикальной плоскости, определяем реакции опор и строим эпюру Мв
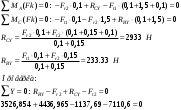
Условно разобьем балку на три участка. На каждом из них мысленно проведем сечение на каком-то расстоянии Z1,Z2,Z3 от характерных точек и рассмотрим изгибающий момент, возникающий в сечении
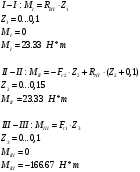

Построим эпюру.
Аналогично будем действовать с горизонтальной плоскостью
21
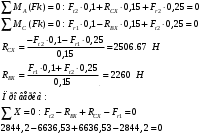
Условно разобьем балку на три участка. На каждом из них мысленно проведем сечение на каком-то расстоянии Z1,Z2,Z3 от характерных точек и рассмотрим изгибающий момент, возникающий в сечении
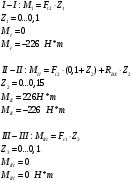
Построим эпюру
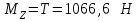
Крутящий момент МZ действует между колесами.
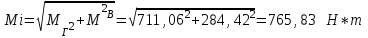
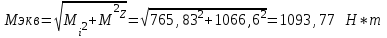

22
Найдем диаметр
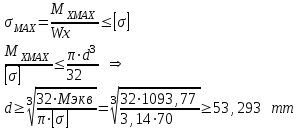
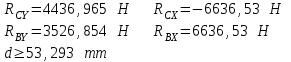
Ответ:

23
Задача 30. Проверит на устойчивость сжатую стойку, если [Sy]=3,5
| Дано: F=55 kH L=3 м Материал – Ст.5 | |
| | |
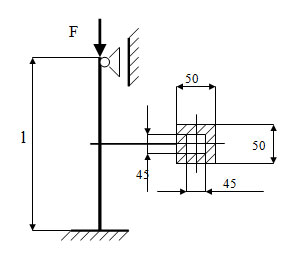
Решение
Условие устойчивости сжатого стержня
Sy=
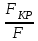
Определяем соответствующее значение коэффициента приведенной длины µ=0,7
Минимальное значение момента инерции площади поперечного сечения стержня:
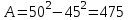
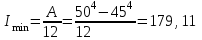
Минимальный радиус инерции сечения
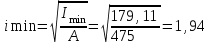
Определим гибкость стержня
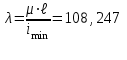
Находим величину предельной гибкости для чугуна, она равна λпред=80

24
Применяем формулу Эйлера т. к. полученная гибкость больше предельной гибкости чугуна. Для чугуна E=1*105 МПа
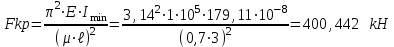
Найдем коэффициент запаса устойчивости
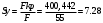
Sy<[Sy]
Отсюда следует, что стойка имеет недостаточный запас устойчивости


 - ?
- ?