лаба 4. ЛАБА 4. Дифракционная решетка
 Скачать 170.92 Kb. Скачать 170.92 Kb.
|
|
Лабораторная работа 4. ДИФРАКЦИОННАЯ РЕШЕТКА Цели работы: исследование дифракции света на прозрачной дифракционной решетке; определение параметров решетки и спектрального состава излучения. Экспериментальная установка (рис. 4.1) состоит из источника света 1 (ртутная лампа), гониометра 4 и дифракционной решетки 6. Излучение лампы освещает щель 2 коллиматора 3 гониометра и дифракционную решетку, установленную в держателе 5 перпендикулярно падающим лучам. Зрительная труба 9 гониометра может поворачиваться вокруг вертикальной оси гониометра. В фокальной плоскости окуляра зрительной трубы наблюдается дифракционный спектр. Угловое положение зрительной трубы определяется по шкале 7 и нониусу 8 лимба гониометра. Цена деления шкалы гониометра 30′, нониуса – 1′. Поскольку начало отсчета по шкале гониометра может не совпадать с направлением нормали к поверхности решетки, то угол дифракции φm определяется разностью двух углов m 0 ( ) − , где 0 – угол, отвечающий центральному m = 0 дифракционному максимуму. Общие сведения Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонением от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Рис. 4.1. Схема экспериментальной установки 25 Различают два вида дифракции. Если лучи света, падающие на препятствие, и лучи, идущие в точку наблюдения, образуют практически параллельные пучки, говорят о дифракции Фраунгофера, в противном случае – о дифракции Френеля. Дифракция Фраунгофера возникает, когда источник и точка наблюдения расположены от препятствия очень далеко или при собирании параллельных лучей линзой. При дифракции на многих однотипных отверстиях в непрозрачном экране проявляется интерференционное взаимодействие дифрагировавших волн. Прозрачная дифракционная решетка представляет собой пластину из прозрачного материала, на поверхности которой нанесено большое число параллельных равноотстоящих штрихов. Ширина прозрачной полосы (щели) b, расстояние между серединами щелей d, общее число щелей N. Пусть на решетку нормально падает плоская монохроматическая волна и дифракционная картина наблюдается на экране Э, установленном в фокальной плоскости линзы Л (рис. 4.2). Рис. 4.2. Дифракционная решетка Строгий расчет дифракционной картины производится по принципу Гюйгенса–Френеля интегрированием излучения вторичных источников в пределах щелей решетки и затем суммирования колебаний, прошедших от всех щелей. Окончательное выражение для интенсивности света, распространяющегося под углом φ к нормали после дифракции на правильной структуре из N щелей, записывается в виде 2 2 0 sin sin δ sinδ u N I I u = (4.1) 26 где u b = (π λ sinφ ) , δ π λ sinφ = ( d ) . Множитель ( ) 2 sinu u характеризует распределение интенсивности в результате дифракции плоской волны на каждой щели и представляет собой функцию распределения интенсивности на экране от одной щели, а множитель ( ) 2 sin Nδ sinδ учитывает интерференцию между пучками, исходящими от всех щелей. Значение 0 I определяет значение потока энергии, излучаемого в направлении φ = 0, т. е. потока энергии недифрагировавшего света. Первый множитель в (4.1) обращается в нуль в точках, для которых b k sinφ= λ , k =1, 2, 3, ... . (4.2) В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю. Распределение интенсивности, обусловленное дифракцией на каждой отдельной щели, изображено на рис. 4.3, б. Второй множитель в (4.1) принимает значения 2 N в точках, удовлетворяющих условию d m sinφ= λ , m =1, 2, 3, ... (4.3) Условие (4.3) определяет положение максимумов интенсивности, называемых главными. Число m дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два. При выполнении условия (4.3) амплитуда световой волны за системой из N щелей возрастает в N раз по сравнению с интенсивностью света, прошедшего через каждую щель, а интенсивность – в 2 N . Между двумя главными максимумами (при одновременном выполнении sin(Nδ) 0 = и sinδ 0 = ) возникает N – 1 минимум, где sin(Nδ) 0 = , но sinδ 0 . Направление добавочных минимумов определяется условием d m p N sinφ = ( )λ (4.4) Здесь p N = − 1, 2, 3, ..., 1 при p N N = 0, ,2 , ... условие (4.4) переходит в (4.3) и вместо минимума формируется максимум. Если считать, что щели излучают по всем направлениям одинаково, то интенсивности главных максимумов будут одинаковыми и равными интенсивности нулевого максимума (рис. 4.3, а). Ширина главных максимумов определяется числом щелей N, а интенсивность каждого из них пропорциональна 2 N . Результирующее распределение интенсивности I представляет 27 собой распределение интенсивности главных максимумов, промодулированное функцией интенсивности одной щели (рис. 4.3, в). 28 а б в Рис. 4.3. Распределения интенсивностей при дифракции света на правильной структуре N щелей Дисперсия и разрешающая способность дифракционной решетки. Положение главных максимумов на экране зависит от длины волны, поэтому если излучение содержит различные длины волн, все максимумы (кроме центрального) разложатся в спектр. Таким образом, дифракционная решетка представляет собой спектральный прибор. Важнейшими характеристиками спектральных приборов служат дисперсия и разрешающая сила. 29 Угловая дисперсия Dφ определяется как φ D = δφ δλ , где δφ – угол между направлениями на дифракционные максимумы m-го порядка, соответствующие излучениям с близкими длинами волн 1 λ и 2 λ , 2 1 δλ= λ λ − . Угловую дисперсию принято выражать в угловых единицах (секундах или минутах) на ангстрем (или нанометр). Из основного уравнения для углов дифракции d m sinφ= λ , переходя к дифференциалам ( d d md cosφ φ= λ ), получаем D d d m d φ = = φ λ cosφ (4.5) Возможность разрешения (раздельного восприятия) двух близких спектральных линий зависит не только от расстояния между ними, но и от ширины спектрального максимума. На рис. 4.4 показана результирующая интенсивность, наблюдаемая при наложении двух близких максимумов. В случае а оба максимума воспринимаются как один. В случае б максимумы видны раздельно. а б Рис. 4.4. Иллюстрация критерия Рэлея: а – линии сливаются; б – линии можно разрешить Критерий разрешения был введен Рэлеем, предложившим считать две спектральные линии разрешенными в том случае, когда максимум для одной длины волны 1 λ совпадает с первым побочным минимумом для другой 2 λ . В этом случае (при равной интенсивности 0 I исследуемых симметричных максимумов) глубина «провала» составляет 0 0,2I . За меру разрешающей способности (разрешающей силы) Rпринимают безразмерную величину, равную отношению длины волны λ , около которой находятся разрешаемые линии, к наименьшему различию в длинах волн 2 1 δλ= λ λ − , которое удовлетворяет критерию Рэлея: =R λ δλ . Для нахождения разрешающей силы дифракционной решетки необходимо учесть, что угловое положение главного максимума для спектральной линии с длиной волны 1 λ должно совпадать с таковым для первого левого побочного минимума (в этом случае в (4.4) p =−1 ) спектральной линии с длиной волны 2 1 λ λ : 1 2 d m m N sinφ = λ ( 1 )λ = − . Откуда 2 2 1 =R mN λ λ -λ λ δλ= = . 30 Указания по подготовке к работе Создайте таблицы (по форме табл. 4.1, 4.2 и 4.3) для записи параметров установки и результатов наблюдений. Таблица 4.1 Измерение углов дифракции для линий цвета* *В протоколе наблюдений должно содержаться три таких таблицы для линий желтого, зеленого и синего цветов. Таблица 4.2 Константы эксперимента Длина волны зеленогоцвета λ λ λ = нм Постоянная решетки d d d = , мкм Длина решетки L, см Число штрихов на решетке N L d = λ 546 5, = = нм с 95% P 1,5 см Таблица 4.3 Определение длины волны и характеристик дифракционной решетки Цвет спектральной линии Угловой коэффициент a a a = Длина волны λ λ λ = нм Порядок спектра, m φ D m d = cosφm мин/нм R mN = = λ λ R, нм Желтая 1 3 Зеленая 1 3 Синяя 1 3 Указания по проведению наблюдений 1. Включить ртутную лампу. Направить коллиматор на ртутную лампу. Наблюдать в зрительную трубу дифракционную картину. Проверить, стоит m 0 1 2 3 α+m α+m φ α α + + m m = − 0 a m = sinφ+m θ cosφ a m = + m θ cosφ a m = − m a m = sinφ−m φ α α − − m m = − 0 α−m α−m 31 ли дифракционная решетка перпендикулярно выходящему из коллиматора пучку лучей. 2. Повернуть зрительную трубу против часовой стрелки вокруг оси гониометра, навести зрительную трубу на желтую спектральную линию 3-го порядка, определить угол α+3 . Затем поворачивать зрительную трубу по часовой стрелке, последовательно совмещая нить окуляра зрительной трубы с яркими спектральными линиями (желтой, зеленой, синей, белой) порядков m = + + + 3; 2; 1;0 (справаотцентральногомаксимумаивцентреего). Определить соответствующие углы α+m и записать их значения для каждого цвета в табл. 4.1. Продолжать далее поворачивать зрительную трубу по часовойстрелке за центральный максимум, последовательно наводить нить зрительной трубы на синюю, зеленую, желтую линии спектра слева от центрального максимума для m = − − − 3; 2; 1;0 . Определить соответствующие углы α−m . Результаты представить в табл. 4.1. Наблюдения по пп. 2, 3 проделать 3 раза для последующей статистической обработки результатов. Запишите длину решетки L с панели установки в табл 4.2. Указания по обработке результатов 1. Выведите формулы погрешностей θa в табл.4.1 и , λi d в пп. 5 и 6. 2. Для каждого значения m = 3; 2; 1;0 в трех таблицах по форме 4.1 рассчитать средние значения углов αm , φ α α m m = − 0 и значения параметра a m i m = sinφ (где λ , i i a d = i =1,2,3 ). Индекс соответствует желтому, i = 2 – зеленому, i = 3 – синему цветам спектральных линий. 3. По полученным выборкам значений i a объема N = 6 по каждой из таблиц по форме 4.1 найти результат косвенного измерения i i i a a a = выборочным методом обработки данных косвенных измерений с доверительной вероятностью P = 95% . Результаты расчетов занести в табл. 4.3. 4. В координатах ( sinφ ; ) m i y a m x m = = = отметить на миллиметровой бумаге положение совместных значений (sinφ ; ) m m для синей, зеленой и желтой линий и через полученные совокупности точек провести аппроксимирующие прямые i y a x = . 5. Используя значение длины волны для зеленой линии в табл. 4.2 рассчитать методом переноса погрешностей постоянную дифракционной решетки d d d = с P = 95 % . Здесь i i d a = , ( 2) i = и 2 2 = + d d a a ( λ λ) ( ) . Результаты расчетов занести в табл. 4.2. i =1 32 6. Используя метод переноса погрешностей, рассчитать длины волн λ λ λ i i i = света, соответствующие желтому i =1 и синему i = 3 участкам спектра ртутной лампы. Здесь λi i = d a , 2 2 λ λ ( ) ( ) i i i i = + d d a a . Результаты расчетов занести в табл. 4.3. 7. По экспериментальным данным трех таблиц по форме 4.1 и соотношению (4.5) определить угловую дисперсию Dφ дифракционной решетки для желтого, зеленого и синего участков спектра для m = 1; 3. Результаты расчетов представить в табл. 4.3. 8. Используя значение длины L и постоянной решетки d (табл. 4.2), рассчитать число штрихов N на решетке. Результат расчета представить в табл. 4.2. 9. По данным табл. 4.2 рассчитать разрешающую способность R решетки для желтого, зеленого и синего участков спектра для m = 1; 3. Результаты расчетов представить в табл. 4.3. 10. Рассчитать минимальный интервал λ длин волн двух близких спектральных линий, которые может разрешить данная решетка, для желтого, зеленого и синего участков спектра для m = 1; 3. Результаты расчетов представить в табл. 4.3. Протокол Наблюдений
Обработка результатов измерений Вывод формулы погрешностей и , (4.6) Т.к. значение m характеризует порядок спектра, то можно принять равным нулю, и если принять , то получим: (4.7) (4.8) (4.9) Для каждого значения в трёх таблицах по форме 4.1 рассчитываем средние значения углов и значения параметра (где , ). Индекс соответствует желтому, - зеленому, - синему цветам спектральных линий. Ввиду того, что снятие показаний производится на виртуальном стенде, при повторных попытках замера углов, значения не изменятся, поэтому можно принять за значение единичного измерения и, следовательно, при данных обстоятельствах . Найдём параметр . Для примера взят угол дифракции желтого цвета третьего порядка. Результаты заносим в таблицы 4.1.1, 4.1.2, 4.1.3 Таблица 4.1.1 Измерение углов дифракции для линий желтого цвета
Таблица 4.1.2 Измерение углов дифракции для линий зеленого цвета
Таблица 4.1.3 Измерение углов дифракции для линий синего цвета
По полученным выборкам значений объема по каждой из таблиц по форме 4.1 найти результат косвенного измерения выборочным методом обработки данных косвенных измерений с . Результаты занести в таблицу 4.3 Для примера приведен расчет углового параметра для зеленого цвета. Находим СКО: при и Находим среднюю приборную погрешность Из таблицы очевидно, что Связано это с уже упомянутым выше фактором виртуального стенда. Значения при m=1 и m=-1 получились равными по модулю, но противоположными по знаку и в сумме каждо такая пара значений противоположных порядков дифракции даёт нуль. Находим полную приборную погрешность : В нашем случае: Как итог, результат косвенного измерения: Аналогично находим угловые коэффициенты для зеленого и синего цветов. Результаты заносим в табл. 4.3. В координатах отметить положение совместных значений для синей, зеленой и желтой линий, и через полученные совокупности точек провести аппроксимирующие прямые График 4.1. Зависимость синуса угла дифракции от порядка дифракции, а также их аппроксимирующая функция для желтого цвета. 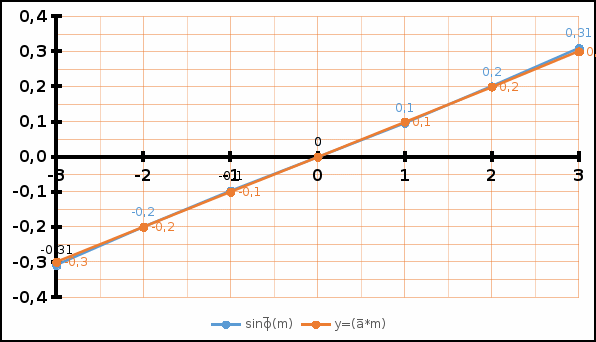 График 4.2. Зависимость синуса угла дифракции от порядка дифракции, а также их аппроксимирующая функция для зеленого цвета. 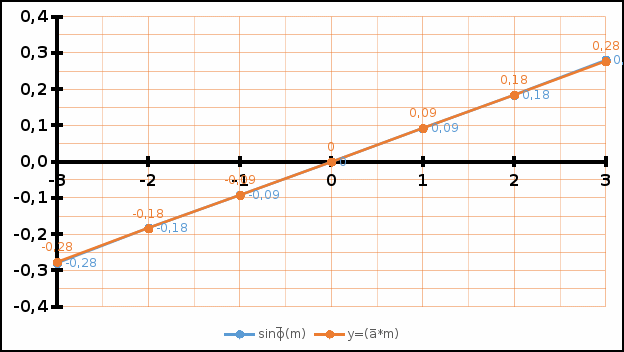 График 4.3. Зависимость синуса угла дифракции от порядка дифракции, а также их аппроксимирующая функция для синего цвета. 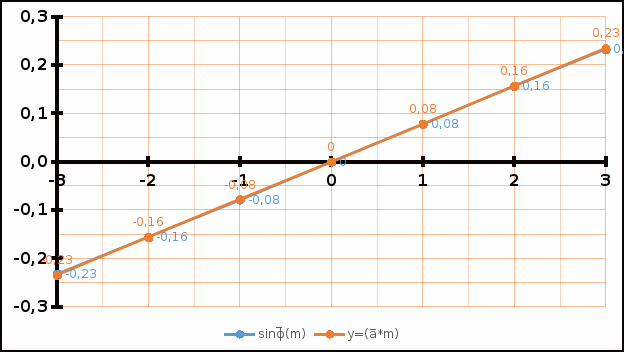 И снова из-за программной природы измерений, зависимость получилась строго линейной и их аппроксимации практически совпали. В случае реального стенда, конечно, зависимость была бы неидеальной и картина получилась бы более информативной с академической точки зрения. Используя значение длины волны для зеленой линии в таблице 4.2 расчитать методом переноса погрешностей постоянную дифракционной решетки . Результаты заносим в табл. 4.2 Таблица 4.2 Константы эксперимента
Используя метод переноса погрешностей, рассчитать длины волн света, соответствующие желтому и синему участкам спектра. Результаты занести в таблицу 4.3. Для примера показан расчёт для желтого участка спектра По экспериментальным данным трех таблиц по форме 4.1 и соотношению (4.5) определить угловую дисперсию дифракционной решетки для желтого, зеленого и синего участков спектра для . Результаты расчетов представить в таблице 4.3. Для примера приведем расчёт для желтого участка спектра третьего порядка: Используя значение длины L и постоянной решетки (таблица 4.2), рассчитать число штрихов N на решетке. Результат расчета представить в таблице 4.2. По данным таблицы 4.2 рассчитать разрешающую способность R решетки для желтого, зеленого и синего участков спектра для . Результаты расчетов представить в таблице 4.3 Для примера приведем расчёт для желтого участка спектра третьего порядка: Рассчитать минимальный интервал длин волн двух близких спектральных линий, которые может разрешить данная решетка, для желтого, зеленого и синего участков спектра для . Результаты расчетов представить в таблице 4.3 Для примера приведем расчёт для желтого участка спектра третьего порядка: Таблица 4.3 Определение длины волны и характеристик дифракционной решетки
|
