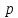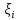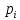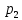Теория вероятностей ПЗ. Теория вероятностей и математическая статистика. Решение По классическому определению вероятности, вероятность события равна где число благоприятных исходов, общее число исходов
 Скачать 22.01 Kb. Скачать 22.01 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Теория вероятностей и математическая статистика Группа Го20Э371 Студент А.И. Ожерельева МОСКВА 2021 Задание №1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет. а) Чему равна вероятность того, что вынимая четыре буквы, получим слово РЕКА? б) Какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение: По классическому определению вероятности, вероятность события 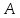 равна равна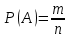 где 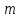 – число благоприятных исходов, – число благоприятных исходов, 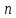 – общее число исходов. – общее число исходов.а) По формуле умножения вероятностей, с учетом того, что буква «А» встречается дважды, вероятность того, что получилось слово РЕКА, равна: 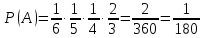 б) Аналогично, вероятность того, что получилось слово КАРЕТА, равна: 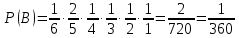 Ответ: 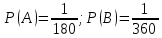 Задание №2. Дискретная случайная величина 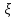 задана следующим законом распределения: задана следующим законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Решение Математическое ожидание 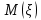 равно: равно: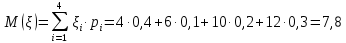 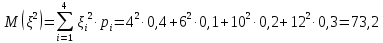 Дисперсия 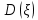 равна: равна: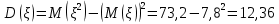 Среднее квадратическое отклонение 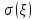 равно равно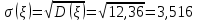 Ответ: 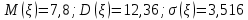 Задание №3. Возможные значения случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание 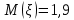 , а так же , а так же 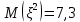 найти вероятности найти вероятности 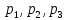 , которые соответствуют дискретным значениям случайной величины. , которые соответствуют дискретным значениям случайной величины.Решение Закон распределения имеет вид:
Математические ожидания 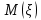 и и 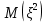 равны: равны: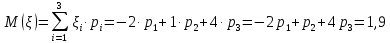 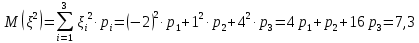 Составим и решим систему: 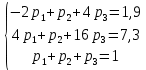 Выражая из третьего уравнения 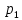 и подставляя его в первые два уравнения, получим: и подставляя его в первые два уравнения, получим: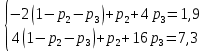 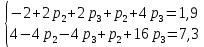 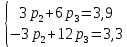 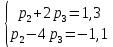 Вычитая из второго уравнения первое, получим: 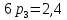 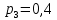 Тогда 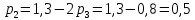 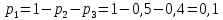 Закон распределения имеет вид:
Ответ: 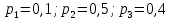 |