a
Материальная точка начинает двигаться из начала координат в момент времени t0 = 0 с нулевой начальной скоростью и ускорением,
изменяющимся со временем по закону
→ ib jkt, где b = 3 м/ с2 , k =
12м / с3 . На каком расстоянии от начала координат окажется точка через время t = 1 c?
Дано
→ ib jkt
a
b = 3 м/ с2 k = 12м / с3 t = 1 c
t0 = 0
|
Решение.
По условию этой задачи имеем закон:
→
a ib jkt
Подставим в него всё, что известно в условии задачи:
→
a i 3 j12 t
В итоге ускорение материальной точки будет равно:
→
a 3 i 12 t j
Тогда для проекций ускорения на координатные оси имеем
аx 3
a 12t.
y
А для проекций скорости на координатные оси имеем
vx 3tdt 3t C1
vy 12tdt 6t C.
2
2
Если в начальный момент времени скорость точки была нулевой, то нулевыми были и проекции скорости на координатные оси. Тогда 3t C1 0,
6t2 C 0.
2
Откуда
C1 0,
C2 0.
Тогда
vx 3t.
2
vy 6t.
Для проекций радиус-вектора точки на координатные оси имеем
x 3tdt 3t C
2 3
y 6t2dt 2t3 C.
4
Если в начальный момент времени точка находилась в начале координат, то
|
Найти S — ?
|

 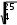 Ответ: S = 2,5 м. Ответ: S = 2,5 м.
Сформулировать уравнения движения частицы массы m: а) в проекциях на оси x,y,z декартовой системы координат; б) в проекциях на направления
касательной и нормали к траектории. Консервативна ли сила
→ → → →
Дано Частица m
оси x,y,z
→ → → →
F axex byey czez
U(x,y,z)
|
Решение.
В любой момент времени для движущейся точки выполняется основное уравнение динамики:
ma F
Вспоминая из кинематики формулу
|
Найти Сформулировать уравнения движения частицы массы m: а) в проекциях на оси x,y,z декартовой системы координат; б) в проекциях на
направления
|
выражающую ускорение через радиус-вектор точки, представим основное уравнение динамики в следующем виде:
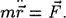
Это равенство, выражающее основное уравнение динамики в дифференциальной форме, называется векторным дифференциальным уравнением движения материальной точки.
Векторное дифференциальное уравнение
|
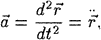 F axex byey czez? В случае положительного ответа найти потенциальную энергию U (x,y,z). F axex byey czez? В случае положительного ответа найти потенциальную энергию U (x,y,z).

касательной и нормали к траектории.
Консервативна ли сила
→ → → →
F axex byey czez
? В случае положительного ответа найти потенциальную энергию U (x,y,z). а) F — ?
б) F — ?
Консервативна ли сила
→ → → →
F axex byey czez
?
U (x,y,z) — ?
|
эквивалентно трем скалярным дифференциальным уравнениям того же порядка. Они получаются, если основное уравнение динамики спроектировать на координатные оси и записать в координатной форме:
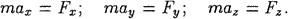
Полученные равенства называются дифференциальными уравнениями движения материальной точки в декартовой системе координат. В этих уравнениях x, y, z- текущие координаты точки, Fx, Fy , Fz — проекции на координатные оси равнодействующей сил, приложенных к точке.
Проектируя основное уравнение динамики на естественные координатные оси, получаем равенства:
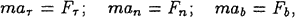
где a , an , ab— проекции ускорения на касательную, главную нормаль и бинормаль траектории в текущем положении
точки; F , Fn , Fb— проекции равнодействующей силы на эти же оси. Вспоминая формулы кинематики для проекций ускорения на естественные оси и подставляя их в написанные равенства, получим:
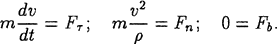
Это дифференциальные уравнения движения материальной точки в естественной форме.
Здесь v— проекция скорости на направление касательной, — радиус кривизны траектории в текущем положении точки.
Консервативные силы — это силы, работа которых не зависит от вида
траектории точки приложения этой силы и закона её движения и определяется только начальным и конечным положением этой точки.
Следовательно сила F axex byey czez
|

Ответ: а)
F axex byey czez; б)
F axex byey czez; эта сила является
2
консервативной (потенциальной); x
Ux, y, z a ex
2
b2 ey
c2 ez
Определить величины
a,→ a, соответствующие изменению
и
a
ано
ектора
|
Решение.
Чтобы найти приращение вектора надо из его конечного значения вычесть начальное. Начальное значение вектора равно а, конечное его значение равно
− а. Тогда изменение вектора Δа = (− а) − а = − 2а. Модуль изменения вектора, очевидно, равен 2а, то есть
| Δа | = 2а.
Найдем изменение модуля вектора: Этого и следовало ожидать, ведь изменилось только направление вектора, а модуль остался прежним, его изменения не произошло.
|
Найти
a — ?
→ — ?
a
a — ?
|
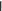 направления вектора а на противоположное. Д вОтвет: Δ а = − 2 а; | Δ а | = 2а; Δа = 0.
Колесо вращается вокруг своей оси симметрии так, что зависимость угла поворота радиуса колеса от времени дается уравнением At Bt2 Ct3
, где А=2 рад/с, В=0,5 рад/с 2 , С=0,5рад/с 3 . Найти радиус R колеса, если в момент времени t = 2 c нормальное ускорение точки на ободе колеса равно an = 36м/ с2 .
Дано
|
Решение.
По условию этой задачи зависимость угла поворота радиуса колеса от времени дается уравнением:
At Bt2 Ct3
Подставляем то, что задано:
2t 0,5t2 0,5t3
Угловая скорость есть:
t
2 t1,5 t2
в момент времени t = 2 с составляет:
t 2 2 2 1,5 22 10 рад/ с.
Линейная скорость связана с угловой по формуле:
v R
Нормальное ускорение вычисляется по формуле:
v2 2 R2 2
an R R R
Тогда радиус колеса можно вычислить по формуле:
R an
2
R 36 0,36м.
100
|
Колесо
|
At Bt2 Ct3
|
А=2 рад/с
|
В=0,5 рад/с 2
|
С=0,5рад/с 3
|
t = 2 c
|
an = 36м/ с2
|
Найти
|
R — ?
|
Ответ: R=0,36 м.
Найти для идеального газа уравнение такого процесса, при котором теплоемкость газа изменяется с температурой по закону С = α/T, где α = const.
Дано Идеальный газ С = α/T
α=const
|
Решение.
Процесс не политропный. Поэтому применив первое начало термодинамики в форме:
Q dU A
для одного моля газа:
dT CdT pdVT V
Используя уравнение Менделеева-Клапейрона перепишем это уравнение в виде
dT CdT RTdVT VV
Разделив левую и правую части на RT, после интегрирования получаем
1 ln T lnV constRT 1
Отсюда находим искомое уравнение процесса:
VT1/( 1)e( / RT) const
|
Найти Найти для идеального
газа уравнение такого процесса, при котором теплоемкость газа изменяется с температурой по закону С = α/T, где α =
const.
|
Ответ: VT1/( 1)e( / RT) const |
 Скачать 38.89 Kb.
Скачать 38.89 Kb.

 Ответ: S = 2,5 м.
Ответ: S = 2,5 м.
 направления вектора а на противоположное. Д
направления вектора а на противоположное. Д 