Гидравлика+. Решение. При нагревании происходит увеличение объема, занимаемого жидкостью v t t v
 Скачать 21.54 Kb. Скачать 21.54 Kb.
|
|
Задача 1. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры tк = (35 +x) °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина tн = (15 + y) °С. Модуль объемной упругости бензина Еж = 1300 МПа, коэффициент температурного расширения βt= 8*10-4 1/град. (tк = 45°С, tн = 16°С) Решение. При нагревании происходит увеличение объема, занимаемого жидкостью: ΔVt = βtV (tк – tн) = βtVΔt. При сжатии происходит уменьшение объема, занимаемого жидкостью: ΔVр = - β рV (рк – рн) = - β рVΔр = - VΔр / Еж. где: β р = 1/ Еж – коэффициент объемного сжатия. Так как канистра абсолютно жесткая, то суммарное изменения объема равно нулю, то есть: ΔVt + ΔVр = 0 или βtVΔt - VΔр / Еж = 0 Откуда: Δр = βtΔt Еж = 1300*8 10-4 (45 - 16) = 30,2 МПа. Определить объемный модуль упругости жидкости, если под действием груза А массой m = 270 кг поршень опустился на расстояние Δh = 5 мм. Начальная высота положения поршня (без груза) Н = 2,5 м, диаметр поршня d = 80 мм, а резервуара D =300 мм, высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким Решение: 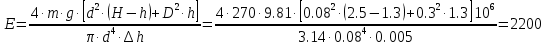 МПа МПаЗадача 3. Воздух поступает в горизонтальную трубу с внутренним диаметром d = 152 мм под давлением p1 = 4,86 МПа при температуре t = 220 °С со скоростью v1 = 60 м/с. Предполагая газ идеальным, а течение изотермическим, найти скорость и расстояние от входа до того сечения, где давление p2 = 1,07 МПа. Принять, что величина коэффициента гидравлического сопротивления постоянна и равна λ = 0,16. Решение: v2 = v1 p2/p1=60*1,07*106/4,86*106=13,2 м/с L = (d/ λ){ (RT/ v1 2 )[1 - (p2/p1) 2 ] - 2 ℓn(p1/p2)} = (0,152/0,016){(287*295/602)[1 – (1,07/4,86)2 ] – 2 ℓn(4,86/1,07)} = 187 м Задача 4. Найти распределение температуры и давления по длине газопровода при установившемся изотермическом в поперечном сечении y течении идеального газа (метана), если объемный расход газа приведенный к нормальным условиям Qат = 20 млн м /сут, плотность ρат = 0,714 кг/м , температура газа при подаче в трубопровод Tн = 324 K, давление pн = 5,4 МПа. Длина газопровода L = 230 км, диаметр d = 720 мм. Температура грунта Tг = 275 K, коэффициент теплопередачи α = 1,5 Вт/м 2 ·град; коэффициент гидравлического сопротивления λ = 0,01. Газовая постоянная метана Rг = 519,625 Дж/кг·град, теплоемкость сp = 2,31 кДж/кг·град. Решение: Определим секундный массовый расход газа Qм = Qат ρат/t = 2*106*0,714/ 86400 = 82,8 кг/с. где t = 24*3600 = 86400 с – продолжительность суток в секундах. Распределение температуры по длине газопровода определяется по формуле Шухова T(x) = Tг + (Tн - Tг) exp[- (απd)/(ср Qм)x] = = 275 +(323 – 275) exp[- (1,5*3,14*0,72)/(2310*82,8)] = 275 + 48exp[- 1,77*10-5 x]. Распределение давления по длине трубопровода определяется по формуле p(x) = {pн 2 – (16λ Qм 2 Rг)/(π2 d 5 )[ xTг + (Tн - Tг) ср Qм/(απd)* *(1 - exp[- (απd)/(ср Qм)x])}1/2 = {(5,4*106 ) 2 – (16*0,01* 82,82 519,625 )/(3,142 0,725 )[ 275x + (323 - 275) 2310*82,8/(1,5*3,14*0,72)(1 - exp[- (1,5*3,14*0,72)/(2310*82,8)x]}1/2 = = {29,2*1012 – 3*105 [ 275x + 27,1*105 (1 - exp[-1,77*10-5 x]}1/2 . Расчеты сведем в таблицу
Задача 5. Определить режим течения и потери давления на трение при перекачке неньютоновской (степенной) жидкости со степенным реологическим законом τ = k(du/dr)n при величине меры консистенции жидкости k = 2,2 Па·с 0,9 и степени нелинейности n = 0,9. Плотность жидкости ρ = 1200 кг/м 3 . Длина горизонтального трубопровода L = 1100 м, внутренний диаметр трубопровода d = 0,5 м, средняя скорость перекачки u = 1м/с. Труба – гидравлически гладкая. Решение: Определяем величину критической скорости перекачки, ниже которой имеет место ламинарный режим течения Uкр = {239,6(2n+1)(5n+3)/(3n+1)/(4n+1)[(3n+1)/n]n k/ρ(2/d)n } 1/(2-n) = ={239,6(2*0,9+1)(5*0,9+3)/(3*0,9+1)/(4*0,9+1)[(3*0,9+1)/0,9]0,9* *1,2/1200/0,250,9} 1/(2-0,9) = 3,27 м/с. Поскольку u < Uкр - режим течения ламинарный. Для заданных условий перекачки определяем число Рейнольдса степенной жидкости Rec = 9,6{(3n+1)/(4n+1)/(2n+1)/(5n+3) )[n/(3n+1)]n ρ(d/2)n u 2-n /k = = 9,6{(3*0,9+1)/(4*0,9+1)/(20,9+1)/(5*0,9+3) )[0,9/(30,9+1)]0,9* *1200*12-0,9*0,250,91 2-0,9 /1,2 = 625,45. Коэффициент гидравлического сопротивления степенной жидкости рассчитывается по формуле λс = 64/ Rec = 64/625,45 = 0,102. Эффективный коэффициент гидравлического сопротивления λэ = 6/5(3n+1)(4n+1)/(2n+1)/(5n+3) λс = = 6/5(3*0,9+1)(4*0,9+1)/(2*0,9+1)/(5*0,9+3) 0,102 = 0,0995. Потери давления рассчитываются по формуле Δp = λэ L/d ρ u2 /2 = 0,0995*1000/0,5*1200*12 /2 = 11,94 кПа. Задача 6. Определить перепад давления при движении по трубопроводу длиной L = (1+0,2x) км диаметром d = 1,1 м вязкопластичной жидкости с начальным напряжением сдвига τ0 = 7,5 Па, пластической вязкостью μp = 0,95 Па*с и плотностью ρ = 1200 кг/м 3 , перекачиваемой со средней скоростью v = 2,83 м/с. Принять, что режим течения – турбулентный. Решение: При турбулентном режиме течения коэффициент гидравлического сопротивления зависит от числа Рейнольдса и числа Хёдстрема, которые определяются выражениями Re = dρv/(2µp) = 1*1200*2,83/(2*0,95) = 1787,4 He = τ0 ρd 2 / µp 2 = 7,5*1200*12 /0,952 = 9972,3. Коэффициент гидравлического сопротивления рассчитывается по формуле 1/λ1/2 = 1/81/2{Re (λ/8)1/2[1 – (1- δ) 4 ]/4 + He(2/λ)1/2 /(3Re)[(1 – δ) 3 – 1] + φ(δ)}, 32 φ(δ) = - 5,714ℓn δ – 2,86 – аппроксимирующая численные расчеты турбулентная составляющая зависимости коэффициента гидравлического сопротивления от безразмерной толщины вязкого подслоя δ, которая определяется выражением δ = 11(λ/8)1/2 Re-1 (1 – ξр) -1 где ξр = 8He Re-2 λ -1 – безразмерный радиус условной стержневой зоны течения. Величина λ, рассчитываемая методом последовательных приближений с использованием трех последних зависимостей, равна λ = 0,052. Потери давления равны Δp = λ L ρv2 /(2d) = 0,052*1000*1200*2,832 /(2*1) = 0,25 Мпа Задача 7. Определить коэффициент проницаемости пористой среды (в Дарси), если известно, что коэффициент фильтрации с = 0,4*10-4 см/с, а кинематический коэффициент вязкости фильтрующейся жидкости ν = 10-6 м /с. Фильтрация жидкости происходит по закону Дарси. Решение: k = с ν/g = 0,4*10-4 *10-6 *104 /981 = 4,06*10-10 см 2 = 4*10-2Д = 40 мД Ответ: k = 40 мД Задача 8. Определить коэффициенты проницаемости и фильтрации для цилиндрических горизонтальных образцов пористой среды диаметром d = 15 см, длиной ℓ= 30 см, если разность давлений на концах образца составляет p1–p2 = 300 мм рт. ст., расход жидкости Q = 1,70 л/ч, динамическая вязкость жидкости μ = 5 мПа*с, плотность ρ = 0,85 г/см 3 . Найти также скорость фильтрации. Решение: Из закона фильтрации Дарси получим, что коэффициент фильтрации определяется выражением с = Q ℓ/(Н1 – Н2)/S где Н1 = p1/( ρg) + z1, Н2 = p2/( ρg) + z2, – полные напоры в начальном и конечном сечениях образца; S =πd2 /4 - площадь поперечного сечения образца. С учетом того, что z1 = z2, а плотность ртути ρрт = 13,6 г/см3 , получим с = Q ℓ ( ρg)/( p1 – p2)/( πd2 /4) = = (1,7*103 /3600)*20*(0,85*981)/(30*13,6*981)/(3,14*152 /4) = 10-3 см/с. Коэффициент проницаемости k и коэффициент фильтрации с связаны соотношением k = с (µ /ρ)/g. С учетом того, что 1Д = 1,02*10-8 см 2 , получим (все единицы переведены в см и с) k = с (µ /ρ)/g = 10-3 *(5*10-3 *104 /850)/981 = 5,99*10-8 см 2 = 5,87Д. Скорость фильтрации определяется выражением w = k( p1 – p2)/( µ ℓ) = 5,99*10-8 *(30*13,6*981)/(5*10-3 *102 *20) =0,024 см/с Задача 9. Определить по формуле Щелкачева, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q = (200+5y) м 3 /сут, мощность пласта h = 5 м, коэффициент пористости m = (16+x) %, коэффициент проницаемости k = 0,2 Д, плотность нефти ρ = 0,8 г/см 3 , динамическая вязкость μ = 5 мПа*с . Скважина гидродинамически совершенна, радиус её rc = 0,1 м. Решение: Определим скорость фильтрации w = Q/(T2πhrc)=200/(24*3600*2*3,14*5*0,1) = 7,372*10-4м/с = 7,372*10-2 см/с. Здесь T = 24*3600 с – продолжительность суток в секундах. Используя величину кинематической вязкости ν = µ/ρ в размерности см 2 /с, определяем число Рейнольдса по Щелкачеву Re=10wk1/2/(m2,3ν)=10*7,372*10-2 *(0,2*1,02*10-8 ) 1/2/(0,162,3*5,88*10-2 ) =0,038. Поскольку Re = 0,038 < Reкр = 1÷ 12, режим течения является ламинарным, а значит, фильтрация в пласте происходит по закону Дарси Задача 10. Определить дебит дренажной галереи шириной В = 100 м, если мощность пласта h = 20 м, расстояние до контура питания ℓ = 11 км, коэффициент проницаемости пласта k = 1 Д, динамический коэффициент вязкости жидкости μ= 1 сП, давление на контуре питания pк = 9,8 МПа и давление в галерее pг = 7,35 МПа. Движение жидкости напорное, подчиняется закону Дарси. Решение: 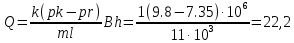 м3/сут м3/сут |
