Решение-1. Решение При выборе регулирующих воздействий руководствуемся следующими соображениями

• Название: Решение При выборе регулирующих воздействий руководствуемся следующими соображениями
• Дата: 01.10.2022
• Размер: 1.47 Mb.
• Имя файла: Решение-1.docx
• Тип: Решение; #708018

Решение

1. 
   При выборе регулирующих воздействий руководствуемся следующими соображениями:
   

а) Регулирующее воздействие должно быть легко осуществимо. Поэтому в качестве таких воздействий выбираем расходы.

b) Регулирующее воздействие должно сильно влиять на регулируемую величину. При оценке влияния руководствуемся значениями коэффициентов усиления, т.к. инерционность каналов примерно одинакова.

Исходя из этого, выбираем следующие регулирующие воздействия:

Для х_см – G₂ (k= -6)

Для L – G₁ (k=5)

Т.к. перекрестное влияние достаточно сильно, требуется дополнительная коррекция. Кроме того, учитывая сильные изменения G₁ по каналу регулирования G₁ – L и G₂ по каналу регулирования G₂ – х_см потребуется ввести каскадную АСР с внутренним расходным контуром.

Структурная схема объекта управления представлена на рис.1

2. 
   Структурная схема системы связанного регулирования представлена на рис. 2.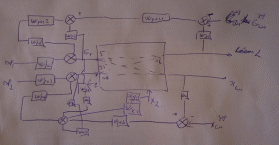
   

3. 
   Принципиальная функциональная схема автоматизации изображена на рис.3.
   

4. 
   Регулирующие органы выбираем из соображений техники безопасности. Это клапаны типа Н3, закрывающиеся при прекращении подачи воздуха. Таким образом, при перебоях в подаче воздуха, смеситель будет отключен от процесса.
   
5. 
   Определим знаки передаточных функций регуляторов и компенсаторов.
   

Исходя из предположения что знаки в сумматорах такие, как изображено на рис.2. Определим знаки передаточных функций регуляторов и компенсаторов из условий реализации отрицательной обратной связи.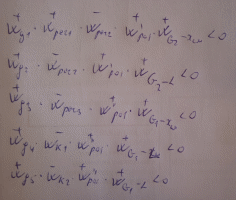

6. 
   Определим передаточные функции реальных компенсаторов.
   

Для определения передаточной функции первого компенсатора запишем передаточную функцию системы по каналу G_2-xсм.



Из условия инвариантности эта передаточная функция должна быть равна нулю, что возможно, если числитель дроби равен нулю.


Первый компенсатор представляет собой усилительное звено, физически реализуем. Имеет коэффициент усиления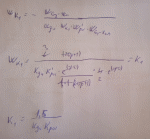



Для определения передаточной функции второго компенсатора запишем передаточную функцию системы по каналу х₂-х_см.



Из условия инвариантности эта передаточная функция должна быть равна нулю, что возможно, если числитель дроби равен нулю. Считая датчики и регулирующие органы усилительными звеньями, получим .Тогда



Первый компенсатор представляет собой сложное звено, физически реализуем, т.к. порядок знаменателя передаточной функции равен порядку числителя. Статический компенсатор имеет коэффициент усиления.

Для получения передаточной функции реального компенсатора сократим два множителя, с близкими постоянными времени.
Таким образом, реальный компенсатор представляет собой усилительное звено.