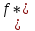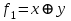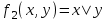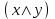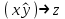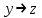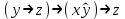КР 4 Булева Алгебра_7. Решение Придаем все аргументам все возможные значения и последовательно заполняем таблицы истинности
 Скачать 374.75 Kb. Скачать 374.75 Kb.
|
|
Вариант 7  Решение: Придаем все аргументам все возможные значения и последовательно заполняем таблицы истинности.
Видим, что таблицы истинности данных формул не совпадают. Значит, данные формулы не равносильны.  Решение: 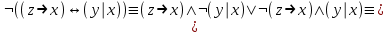 (воспользовались выражением штриха шефера через конъюнкцию и отрицание) (воспользовались выражением штриха шефера через конъюнкцию и отрицание)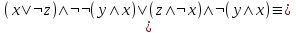 (закон двойного отрицания и закон Моргана) (закон двойного отрицания и закон Моргана)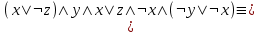 (законы поглощения) (законы поглощения)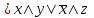 Получили ДНФ нашей формулы. Она не является СДНФ, так как в каждом конъюнкте не все переменные. Построим СДНФ: 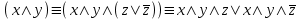 ; ;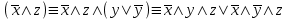 ; ;Подставляем, получаем СДНФ 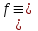 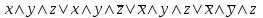 Теперь представим ту же функция в виде КНФ и СКНФ. Для этого берем полученную ДНФ 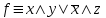 и преобразовываем, используя дистрибутивность, и преобразовываем, используя дистрибутивность,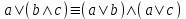 ;получаем: ;получаем: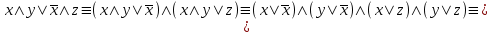 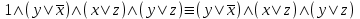 (воспользовались законом исключенного третьего и правилом работы с константой) Получили КНФ данной функции. Она не является СКНФ, так как в каждом дизъюнкте не все три переменные. Преобразуем каждый дизъюнкт: 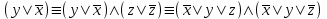 ; ;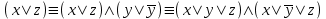 ; ;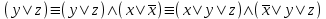 Подставляем, убираем повторяющиеся дизъюнкты (последние 2), получаем СКНФ: 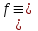 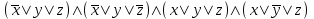 Строим контактную схему СДНФ. СДНФ у нас 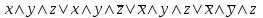 (параллельно соединяем 4 последовательных цепей, соответствующих конъюнктам СДНФ) 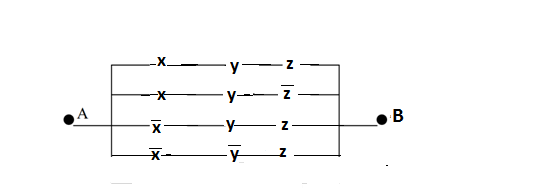 Строим контактную схему СКНФ. 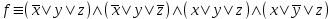 (последовательно соединяем 4 параллельных участка цепи, соответствующих дизъюнктам СКНФ) 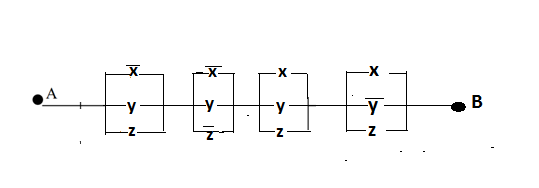 Строим многочлен Жегалкина. Будем преобразовывать ДНФ 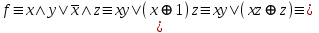 (закон Моргана и закон исключенного третьего) (закон Моргана и закон исключенного третьего) 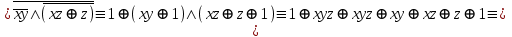 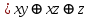 Ответ: СДНФ: 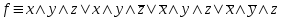 ; ;СКНФ: 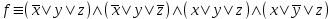 ; ; Многочлен Жегалкина: 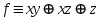  Решение: Таблица истинности:
По строкам где значение функции единица составляем СДНФ: 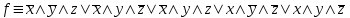 Далее, по строкам, где значение функции ноль составляем CКНФ: 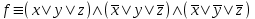 Минимизируем СДНФ. В последнем столбце будем ставить, принадлежит ли соответствующий конъюнкт в предпоследнем столбце полученной СДНФ. Если не принадлежит, ставим *в последнем столбце и во всех клетках соответствующей строки вычеркиваем её. Затем вычеркиваем вычеркнутые в какой-либо строке конъюнкты и в остальных строках такие же. Потом из каждой строки оставшейся выбираем конъюнкт с наименьшим числом переменных 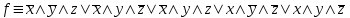
Осталось 4 строчки без *, из каждой выбираем конъюнкт с наименьшим числом переменных (если он уже выбран, переходим к след. строке). В 5 строке получилось 2 выбранных конъюнкта. Это нормально. Поскольку у нас 5 строк и все конъюнкты без звездочек встречаются не более 2 раз, нужно выбрать минимум 3 из них, чтобы из каждой строки был хоть один. Получили минимальную ДНФ: 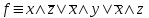 . .Теперь строим минимальную КНФ. Для этого рассматриваем двойственную функцию. У неё будет таблица истинности:
Значит, снова по теоремам Шеннона, СДНФ двойственной имеет вид: 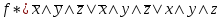 Строим её минимальную ДНФ:
Получаем МДНФ двойственной функции: 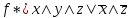 ; ;И по ней строим двойственную функцию. Получаем МКНФ исходной функции: 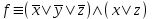 Ответ: СДНФ: 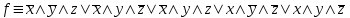 СКНФ: 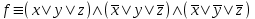 МДНФ: 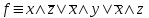 МКНФ: 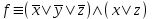 . .Решение: Обозначим для краткости 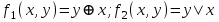 . Записываем их таблицы истинности: . Записываем их таблицы истинности:
По теореме Поста, достаточно проверить, лежат ли наши функции целиком в одном из замкнутых классов. По таблице истинности видим, что 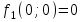 , то есть первая функция сохраняет ноль. , то есть первая функция сохраняет ноль. 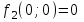 . То есть, обе функции лежат в классе функций, сохраняющих ноль. Значит, данная система не является полной (и, в том числе, не образует базис). . То есть, обе функции лежат в классе функций, сохраняющих ноль. Значит, данная система не является полной (и, в том числе, не образует базис).Ответ: не является. 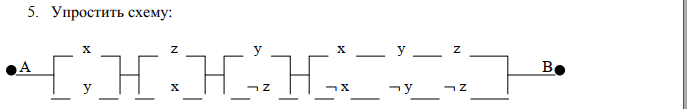 Решение: Запишем формулу соответствующую этой схеме: 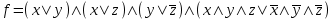 ; ;Преобразовываем эту формулу. Сначала раскрое первые 2 скобки 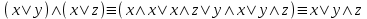 (по закону поглощения). (по закону поглощения).Умножаем на 3-юю скобку. 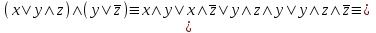 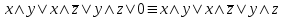 . Теперь умножим это на последнюю скобку . Теперь умножим это на последнюю скобку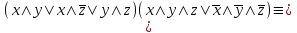 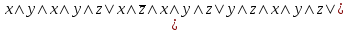 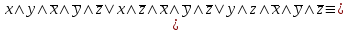 (закон противоречия) (закон противоречия)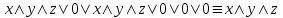 . Понятно, что никак ещё проще не запишешь. . Понятно, что никак ещё проще не запишешь.Получаем упрощенную эквивалентную схему 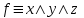 : : Решение: Введем обозначения для утверждений: 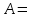 ” земля вращается вокруг Юпитера”; ” земля вращается вокруг Юпитера”; 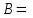 ”завтра начнется зомби апокалипсис”. ”завтра начнется зомби апокалипсис”.Конъюнкция 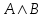 : Земля вращается вокруг Юпитера и завтра начнется зомби апокалипсис. : Земля вращается вокруг Юпитера и завтра начнется зомби апокалипсис.Дизъюнкция: 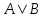 : Земля вращается вокруг Юпитера или завтра начнется зомби апокалипсис (или и то и другое). : Земля вращается вокруг Юпитера или завтра начнется зомби апокалипсис (или и то и другое).Импликация: 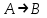 : Если Земля вращается вокруг Юпитера то завтра начнется зомби апокалипсис. : Если Земля вращается вокруг Юпитера то завтра начнется зомби апокалипсис.Эквивалентность 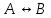 : : Земля вращается вокруг Юпитера в том и только том случае, если завтра начнется зомби апокалипсис. Штрих Шеффера 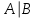 : Или Земля не вращается вокруг Юпитера, или завтра не начнется зомби апокалипсис (или и то и другое). : Или Земля не вращается вокруг Юпитера, или завтра не начнется зомби апокалипсис (или и то и другое). Стрелка Пирса: 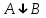 : Земля не вращается вокруг Юпитера и завтра не начнется зомби апокалипсис. : Земля не вращается вокруг Юпитера и завтра не начнется зомби апокалипсис.Решение: Построим таблицу истинности данной формулы: 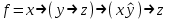
(если заключение верно, то импликация истинна, независимо от посылки) Видим, в последнем столбце все единицы, Значит, наша формула является тождественно истинной.  Решение: Обозначим утверждения: 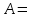 ”капиталовложения останутся постоянными”; ”капиталовложения останутся постоянными”;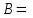 ”правительственные расходы возрастут”; ”правительственные расходы возрастут”;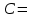 ”возникнет безработица”: ”возникнет безработица”: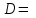 ”налоги будут снижены”. ”налоги будут снижены”.Тогда схема рассуждений имеет вид: 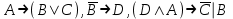 Слева 3 посылки, справа заключение. Чтобы выяснить, является ли заключение верным, можно показать, что всегда, когда истинны посылки, истинно и заключение. Чтобы доказать, что умозаключение неверно, достаточно привести пример истинностных значений переменных, когда посылки истинны, а заключение ложно. Сделаем последнее. Пусть 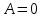 , то есть капиталовложения не останутся постоянными. , то есть капиталовложения не останутся постоянными.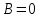 , то есть правительственные расходы не возрастут. Ну и доопределим , то есть правительственные расходы не возрастут. Ну и доопределим 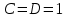 . .Тогда первая посылка верна 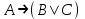 , так как ложна посылка в импликации, , так как ложна посылка в импликации,Вторая посылка 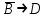 тоже верна, так как истинно заключение D, третья посылка тоже верна, так как истинно заключение D, третья посылка 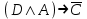 снова верна, так как ложна посылка в импликации. Все три посылки верны, но заключение B ложно. Итак доказали, что данное умозаключение не является правильным. Можно показать, что данное умозаключение станет верным, если добавить дополнительную посылку, что капиталовложения останутся постоянными. снова верна, так как ложна посылка в импликации. Все три посылки верны, но заключение B ложно. Итак доказали, что данное умозаключение не является правильным. Можно показать, что данное умозаключение станет верным, если добавить дополнительную посылку, что капиталовложения останутся постоянными.Решение: Будем рассуждать от противного. Предположим, что существует такой набор истинностных значений переменных, на котором формула 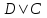 ложна. На этом наборе формулы ложна. На этом наборе формулы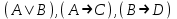 все три являются истинными (так как они тождественно истинны). все три являются истинными (так как они тождественно истинны). Значит истинна и их конъюнкция 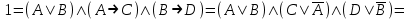 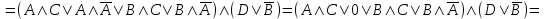 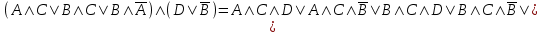 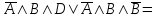 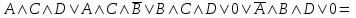 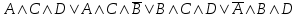 . .Однако, раз 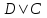 ложна, получаем, что на рассматриваемом наборе ложна, получаем, что на рассматриваемом наборе 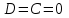 .Но тогда каждый из 4 дизъюнктов ложен, а в итоге дизъюнкция истинна. Противоречие. Значит, наше предположение не верно, что и значит, что формула .Но тогда каждый из 4 дизъюнктов ложен, а в итоге дизъюнкция истинна. Противоречие. Значит, наше предположение не верно, что и значит, что формула 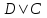 тождественно истинна. тождественно истинна. |

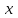
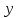
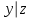
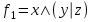
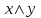
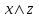
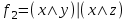
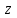
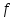
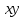 *
*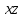 *
* *
* *
* *
*
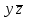
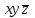
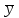 *
*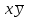 *
*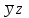 *
*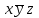 *
*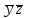 *
*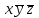
 *
*
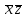 *
*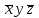
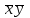 *
*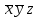
 *
*