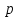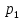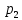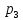теория вероятнестей 2 курс. теория вероятностей. Решение. Применим классическое определение вероятности число благоприятных исходов число всевозможных исходов
 Скачать 19.42 Kb. Скачать 19.42 Kb.
|
|
Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» 1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет. а) Чему равна вероятность того, что вынимая четыре буквы, получим слово РЕКА; б) какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение. Применим классическое определение вероятности: 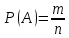 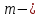 число благоприятных исходов. число благоприятных исходов.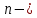 число всевозможных исходов. число всевозможных исходов. а) Из 6 карточек с буквами выбирают четыре; так как последовательность карточек важна, то 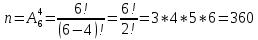 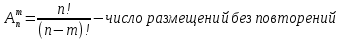 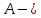 получится слово «река». получится слово «река».Буква «А» повторяется дважды, поэтому возможны перестановки, при которых слово не изменяется. 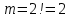 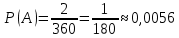 б) Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие 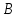 состоит в получении нужного слова «карета». Элементарные события являются перестановками из 6 букв, значит, имеем состоит в получении нужного слова «карета». Элементарные события являются перестановками из 6 букв, значит, имеем 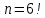 Буква «A» повторяется 2 раза, поэтому возможны перестановки, при которых слово не изменяется. Их число равно 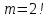 Таким образом: 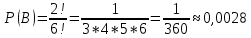 Ответ: а) 1/180; б) 1/360. 2. Дискретная случайная величина 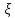 задана следующим законом распределения. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение. задана следующим законом распределения. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение.
Решение. Математическое ожидание: 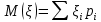 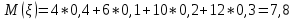 Дисперсия: 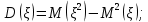 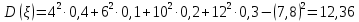 Среднее квадратическое отклонение: 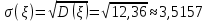 Ответ: 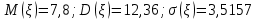 3. Возможные значения дискретной случайной величины равны: -2; 1; 4. При условии, что заданы математическое ожидание 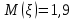 , а также , а также 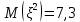 , найти вероятности , найти вероятности 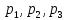 , которые соответствуют дискретным значениям случайной величины. , которые соответствуют дискретным значениям случайной величины.Решение. Закон распределения:
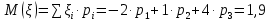 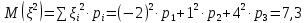 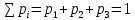 Решая систему трех уравнений с тремя неизвестными: 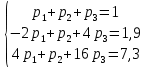 получаем: 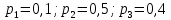 Ответ: 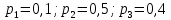 |