теор. Решение. Пронумеруем узлы и стержни фермы
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
 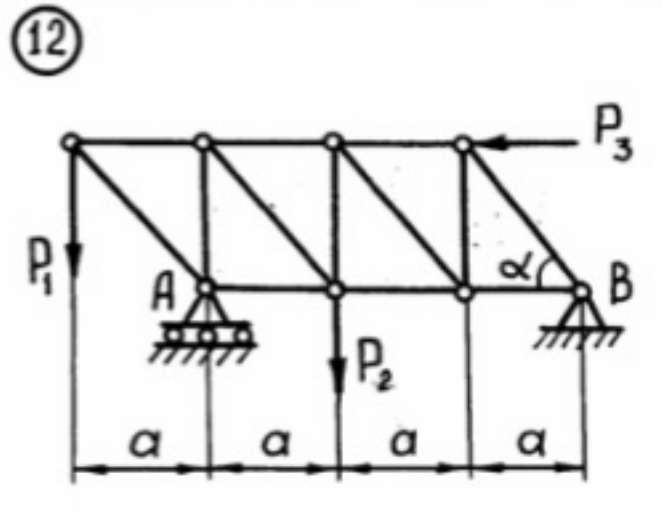 Дано: 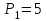 кН, кН, 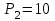 кН, кН, 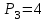 кН, кН, 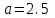 м, м, 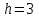 м. м. 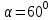 Определить опорные реакции и усилия в стержнях методом вырезания узлов, и методом сквозных сечений. 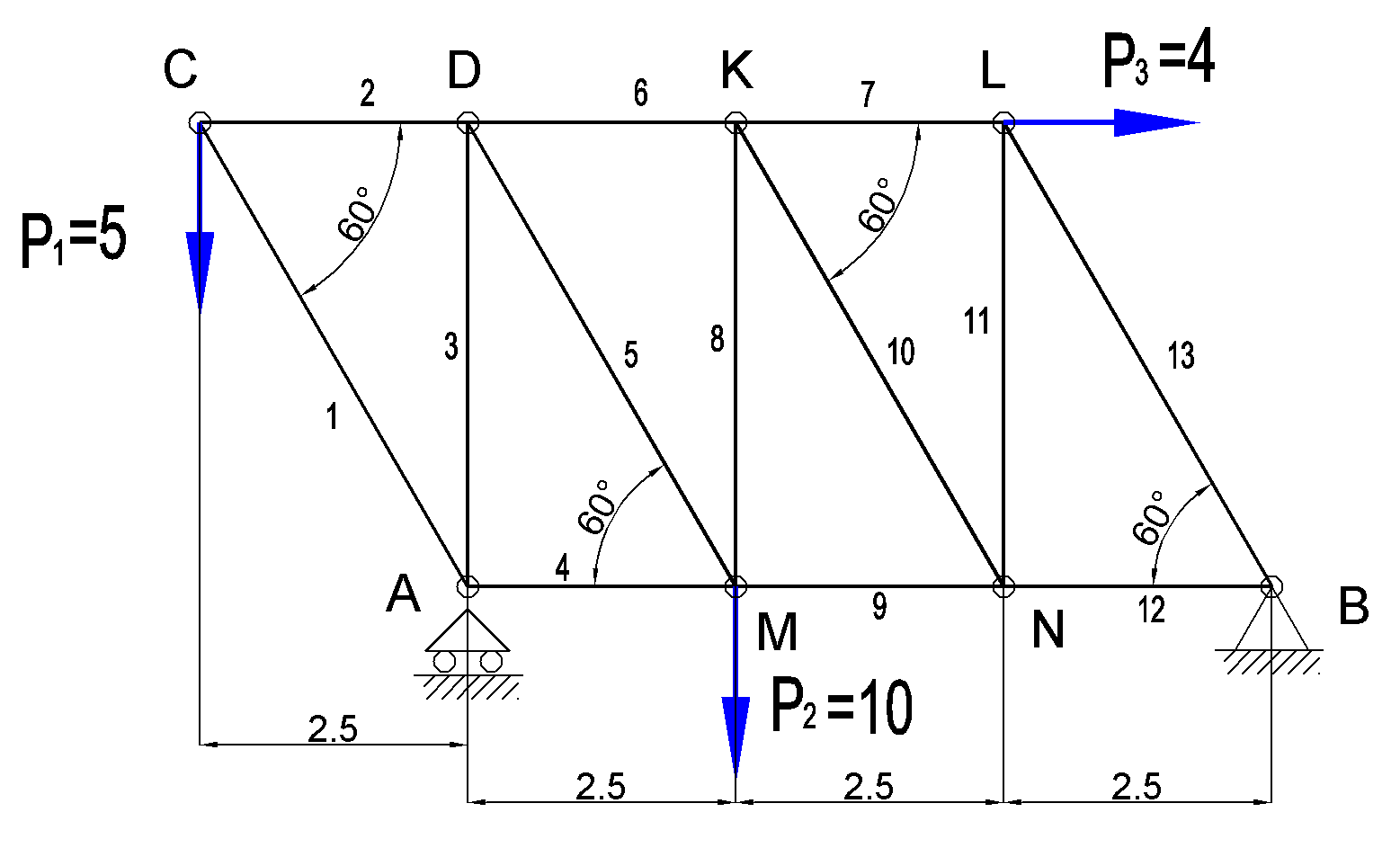 Рис. 1 Решение. Пронумеруем узлы и стержни фермы Узлы фермы (n) нумеруем римскими цифрами, а стержни фермы (m) – арабскими. m = 13; n = 8. 2. Проверим ферму на геометрическую жёсткость и статическую определимость Ферма считается жёсткой и статически определимой, если выполняется условие: m = 2 n – 3. 7 = 2 *8 – 3,7=12,3 Условие выполнено, следовательно, ферма является геометрически жёсткой и статически определимой. При определении опорных реакций ферма рассматривается как твёрдое тело. Опоры в узлах А и В мысленно отбрасываются и заменяются соответствующими реакциями: 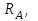 в узле А, составляющие в узле А, составляющие 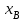 и и 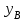 в узле В (рис. 2). в узле В (рис. 2).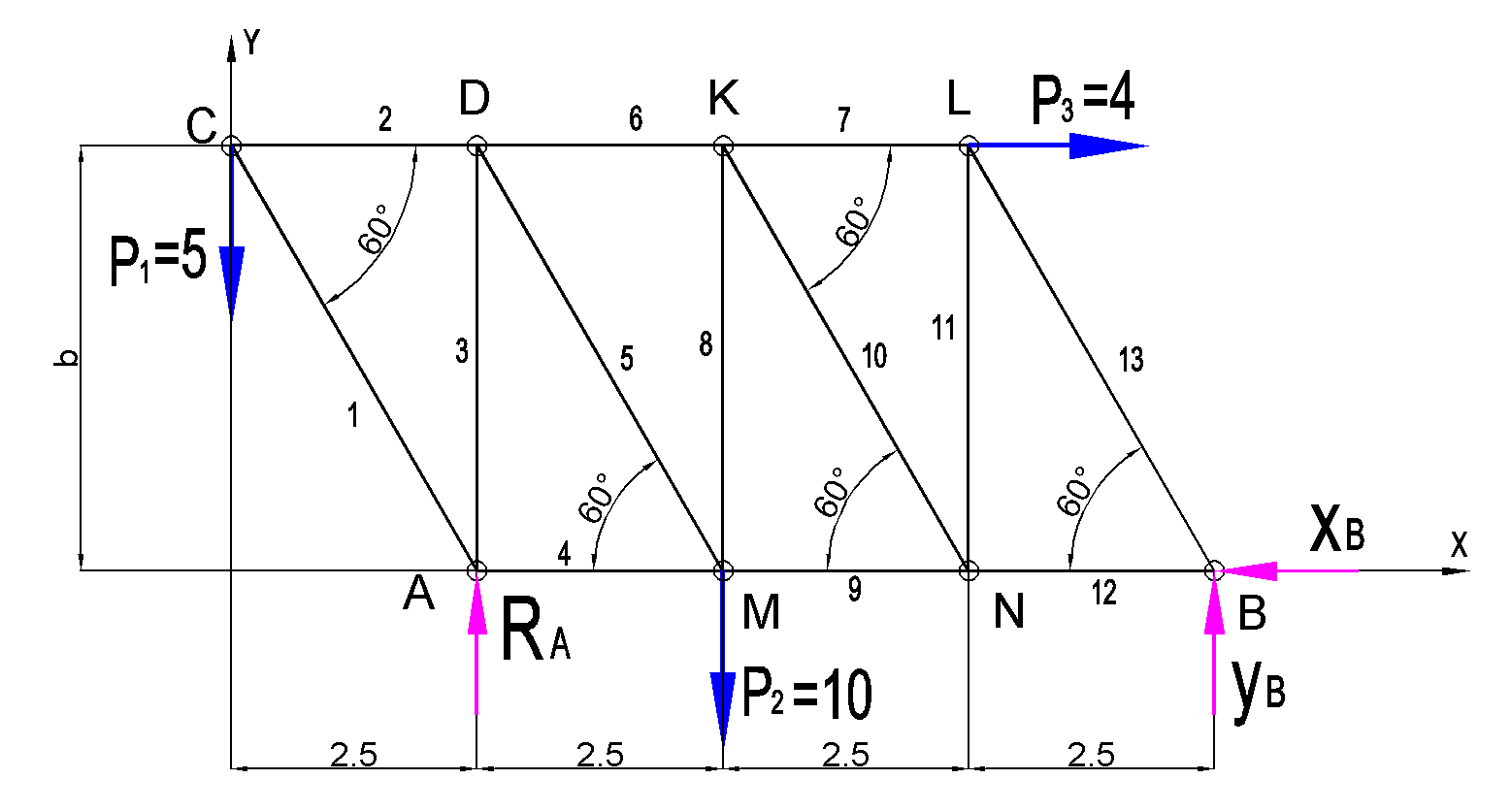 рис. 2 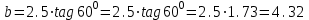 м мСоставляются три уравнения равновесия: 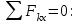 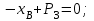 (1) (1) 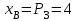 Кн Кн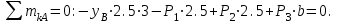 (2) (2)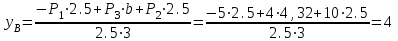 кН кН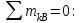 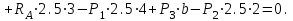 (3) (3)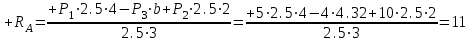 Кн КнПроверка 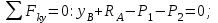 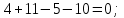 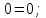 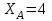 Кн. Кн. 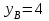 кН. кН. 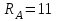 Кн КнПри определении усилий в стержнях методом вырезания узлов сначала мысленно вырезается узел C (в нём сходятся два стержня, усилия в которых неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 3). 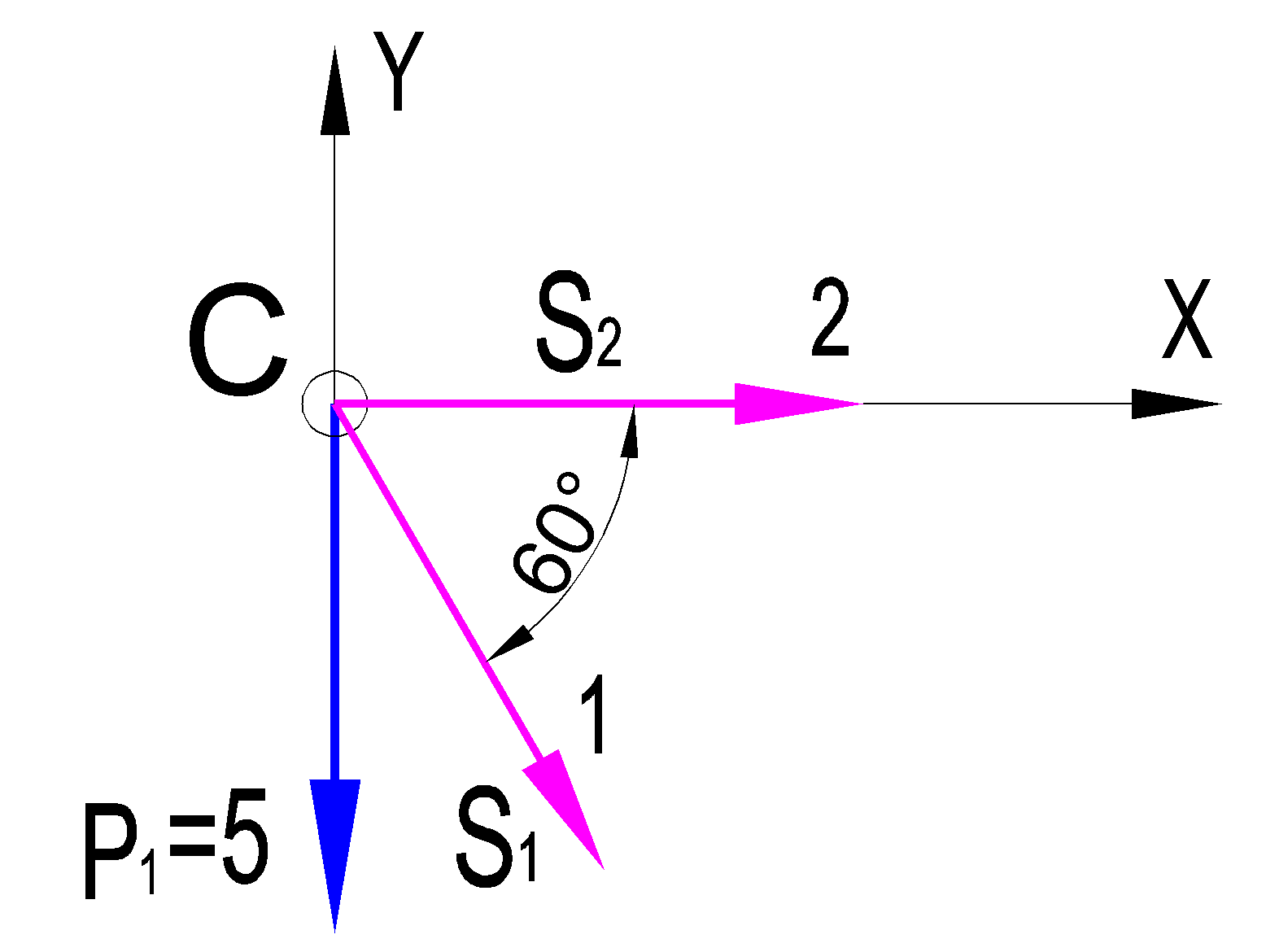 рис. 3 здесь неизвестны усилия 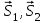 ; ;Составляются уравнения равновесия: 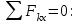 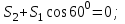 (4) (4)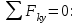 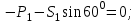 (5) (5)Из (5) 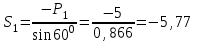 Кн КнИз (4) 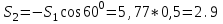 Кн КнПри определении усилий в стержнях методом вырезания узлов сначала мысленно вырезается узел А (в нём сходятся 4 стержня, усилия в двух неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 4). 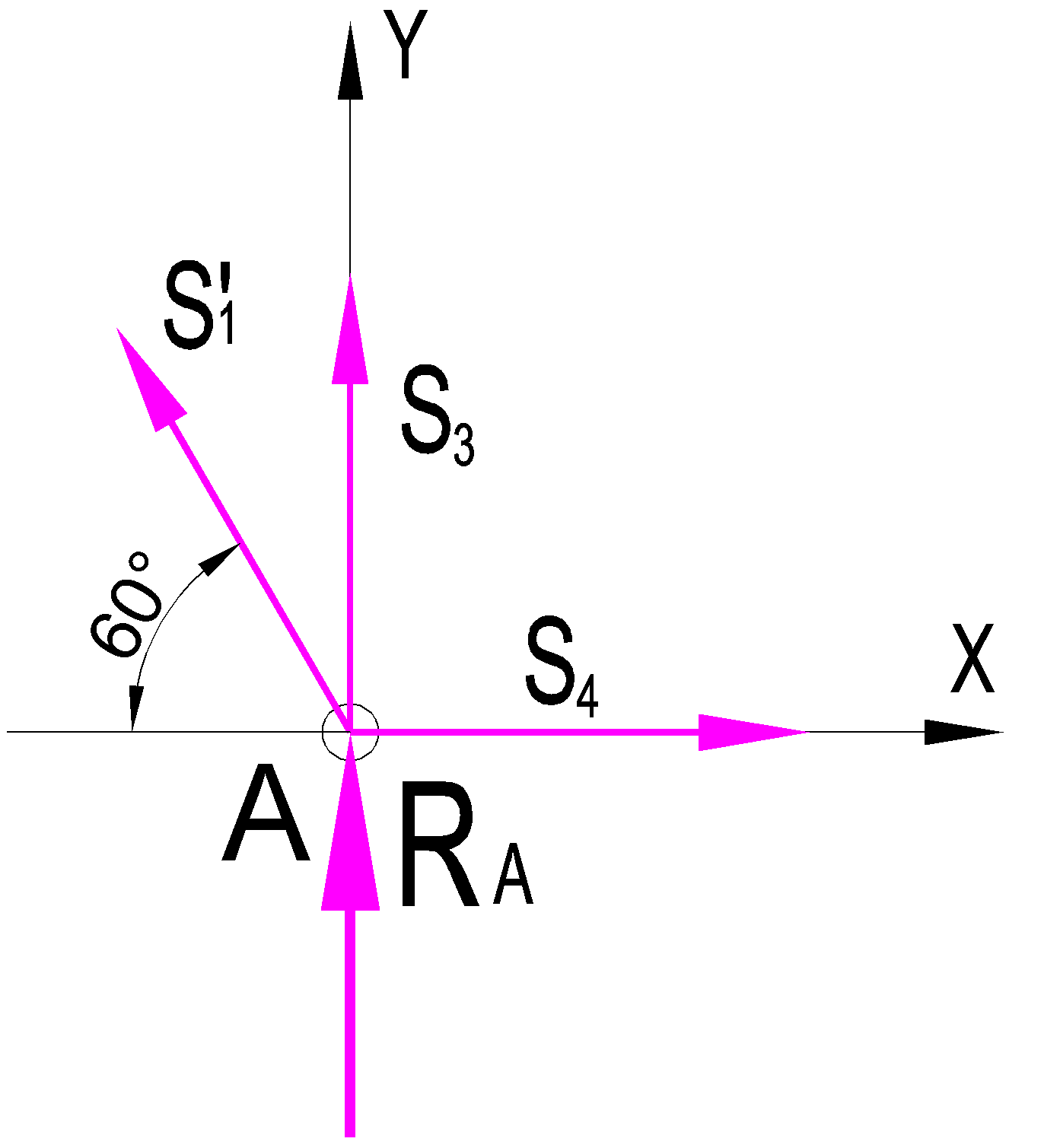 Рис. 4 здесь неизвестны усилия 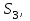 ; ; 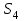 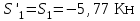 Составляются уравнения равновесия: 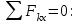 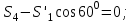 (6) (6)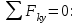 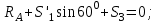 (7) (7)Из (7) 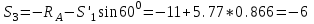 Кн КнИз (6) 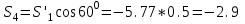 Кн КнВырезается узел D (в нём сходятся 4 стержня, усилия в 2-х неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 5). 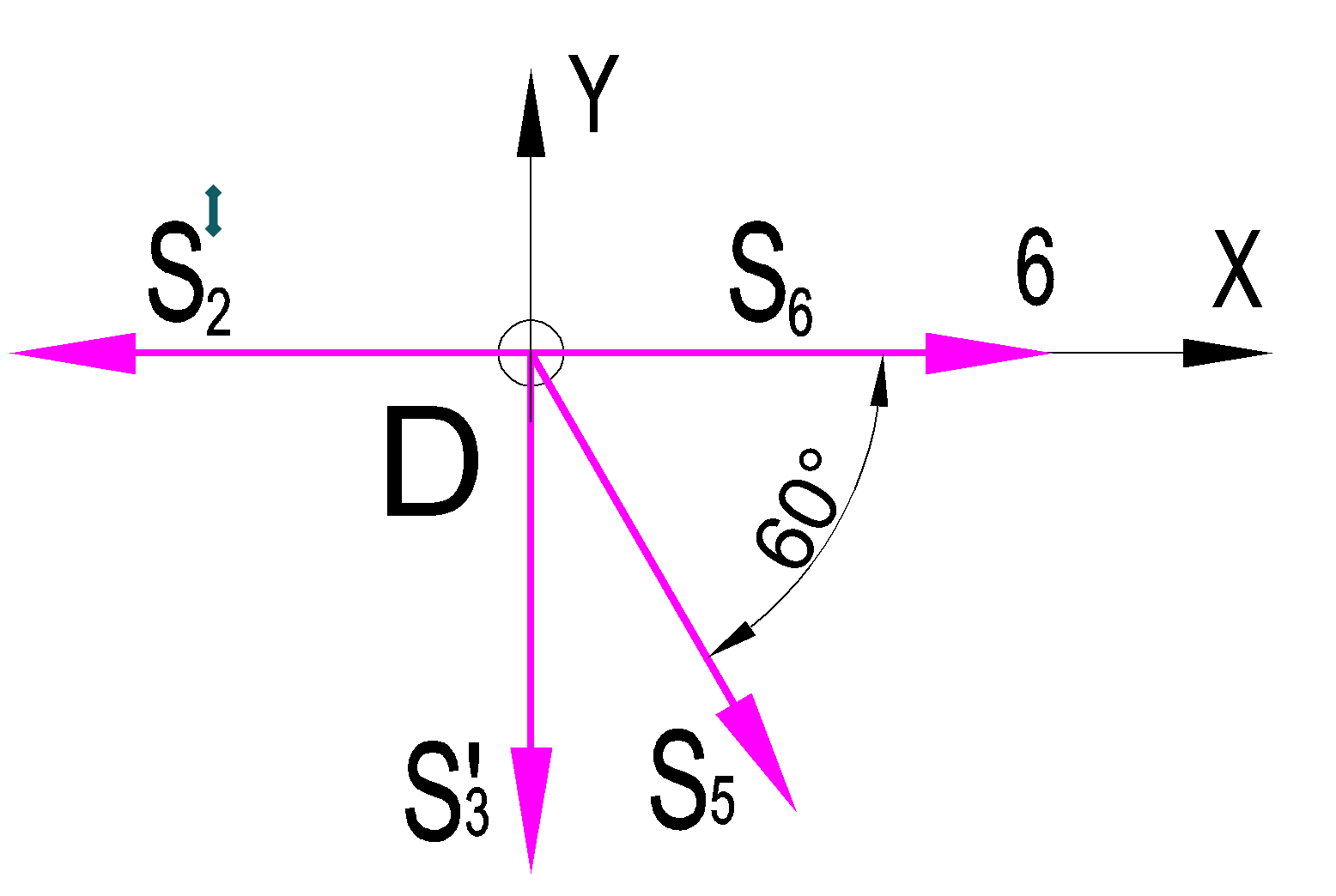 Рис. 5 здесь неизвестны усилия 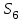 ; ; 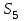 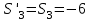 Кн КнСоставляются уравнения равновесия: 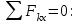 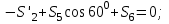 (8) (8)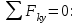 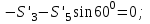 (9) (9)Из (9) 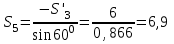 Кн КнИз (8) 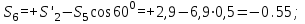 Кн КнВырезается узел M (в нём сходятся 4 стержня, усилия в 2-х неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 6). 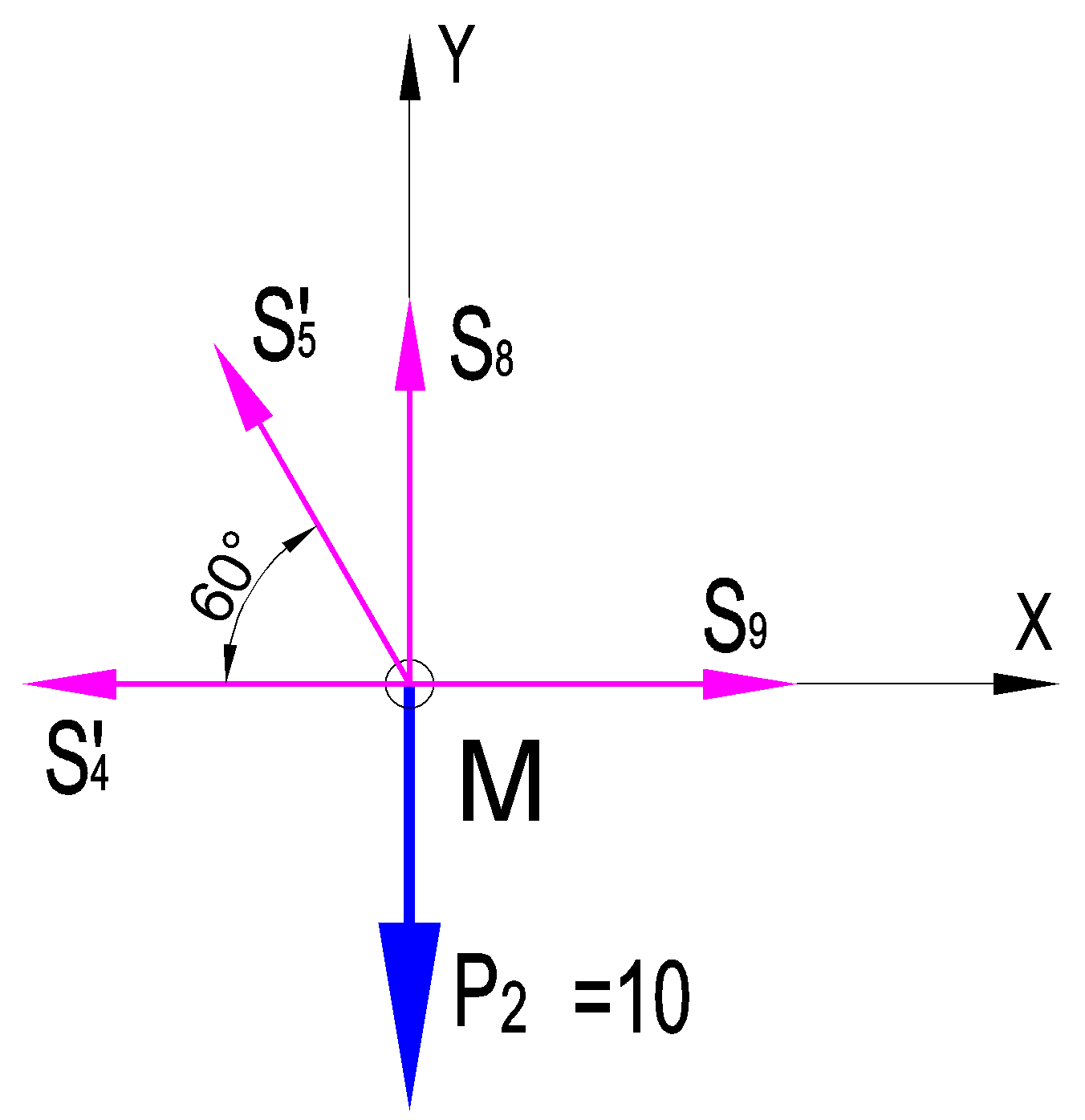 Рис. 6 здесь неизвестны усилия 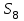 ; ; 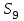 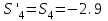 Кн Кн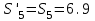 Кн КнСоставляются уравнения равновесия: 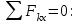 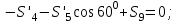 (10) (10)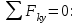 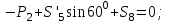 (11) (11)Из (11) 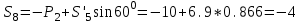 Кн КнИз (10) 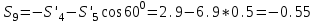 Кн КнВырезается узел K (в нём сходятся 4 стержня, усилия в 2-х неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 7). 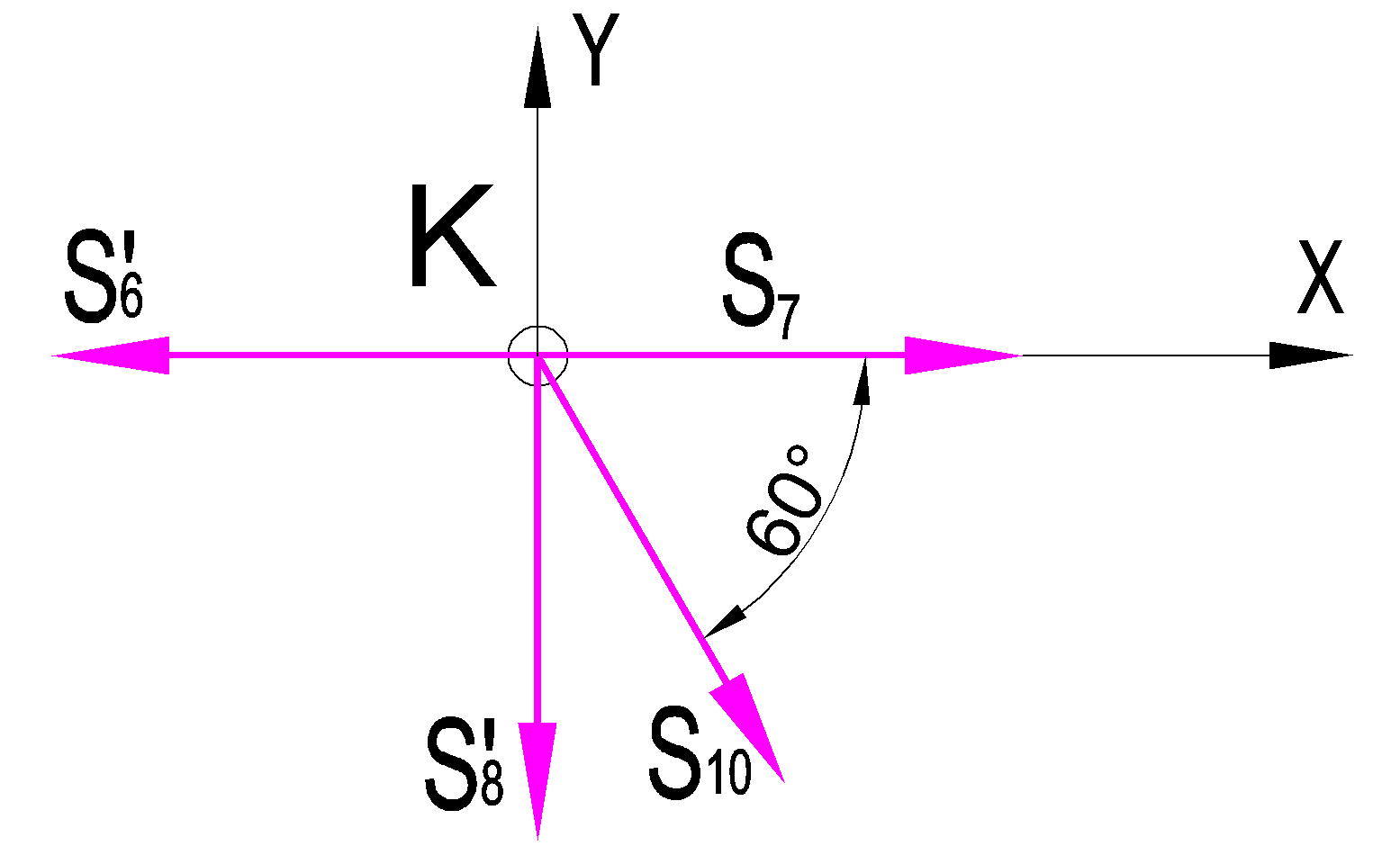 рис. 7 здесь неизвестны усилия 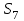 ; ; 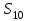 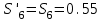 Кн Кн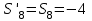 Кн КнСоставляются уравнения равновесия: 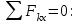 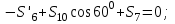 (12) (12)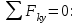 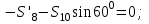 (13) (13)Из (13) 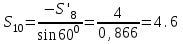 Кн КнИз (12) 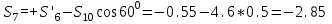 Кн КнВырезается узел N (в нём сходятся 4 стержня, усилия в 2-х неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 8). 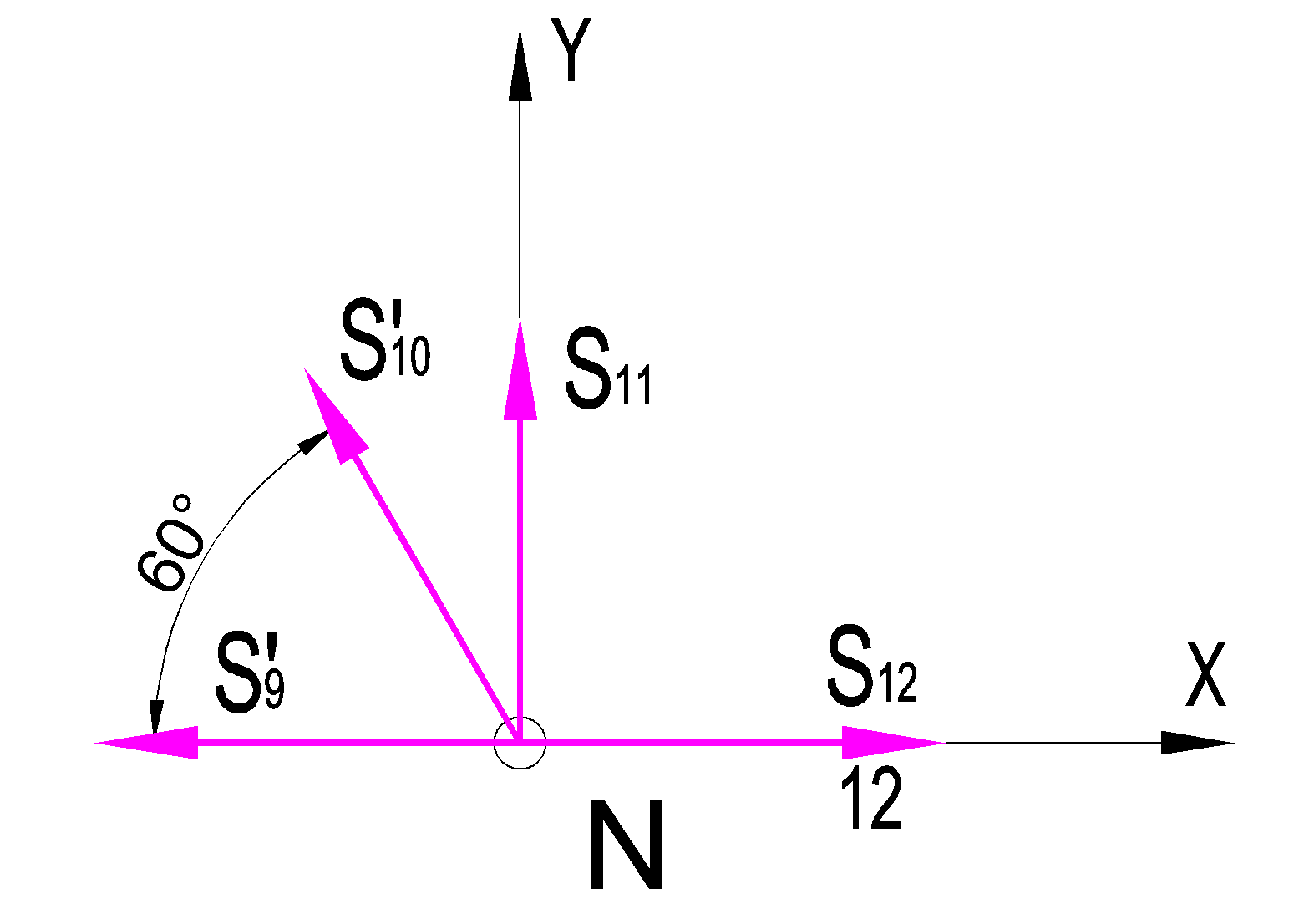 рис. 8 здесь неизвестны усилия 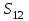 ; ; 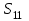 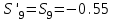 Кн Кн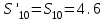 Кн КнСоставляются уравнения равновесия: 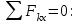 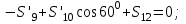 (14) (14)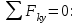 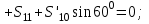 (15) (15)Из (15) 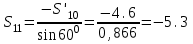 Кн КнИз (14) 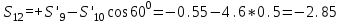 Кн КнВырезается узел B (в нём сходятся 2 стержня, усилия в 1 неизвестны), и изображаются все приложенные к нему силы и реакции (рис. 9). 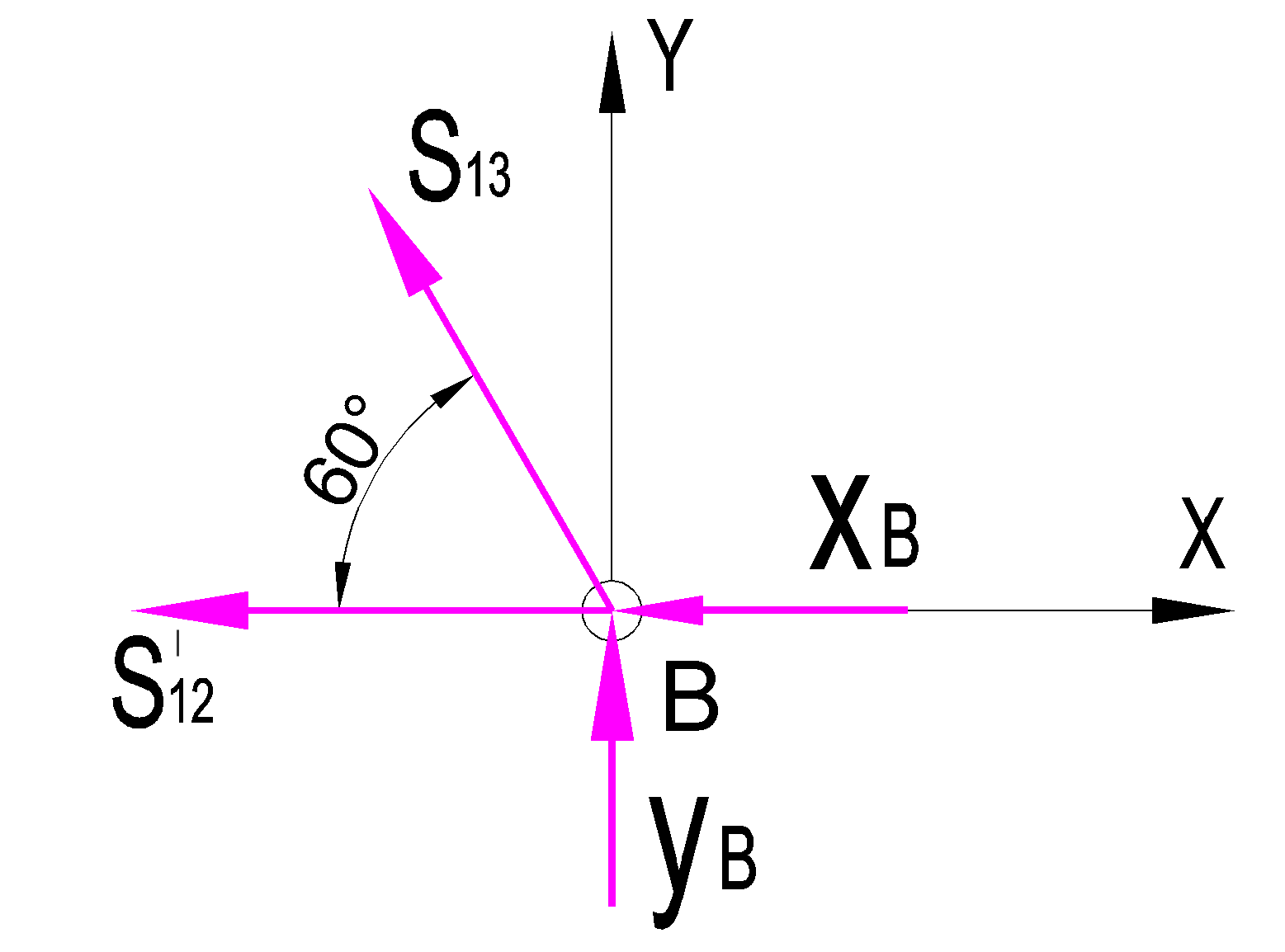 рис. 9 здесь неизвестны усилия 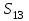 ; ; 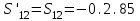 Кн Кн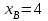 Кн. Кн. 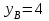 Кн КнСоставляются уравнения равновесия: 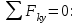 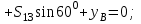 (15) (15)Из (15) 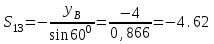 Кн КнПри определении усилий в стержнях методом Риттера ферма рассекается по этим 2-м стержням на две части (1-1). Одна из частей вместе с приложенными к ней нагрузками мысленно отбрасывается, а её действие на оставшуюся часть заменяется усилиями, которые направлены вдоль соответствующих стержней в сторону отброшенной части (рис. 10). 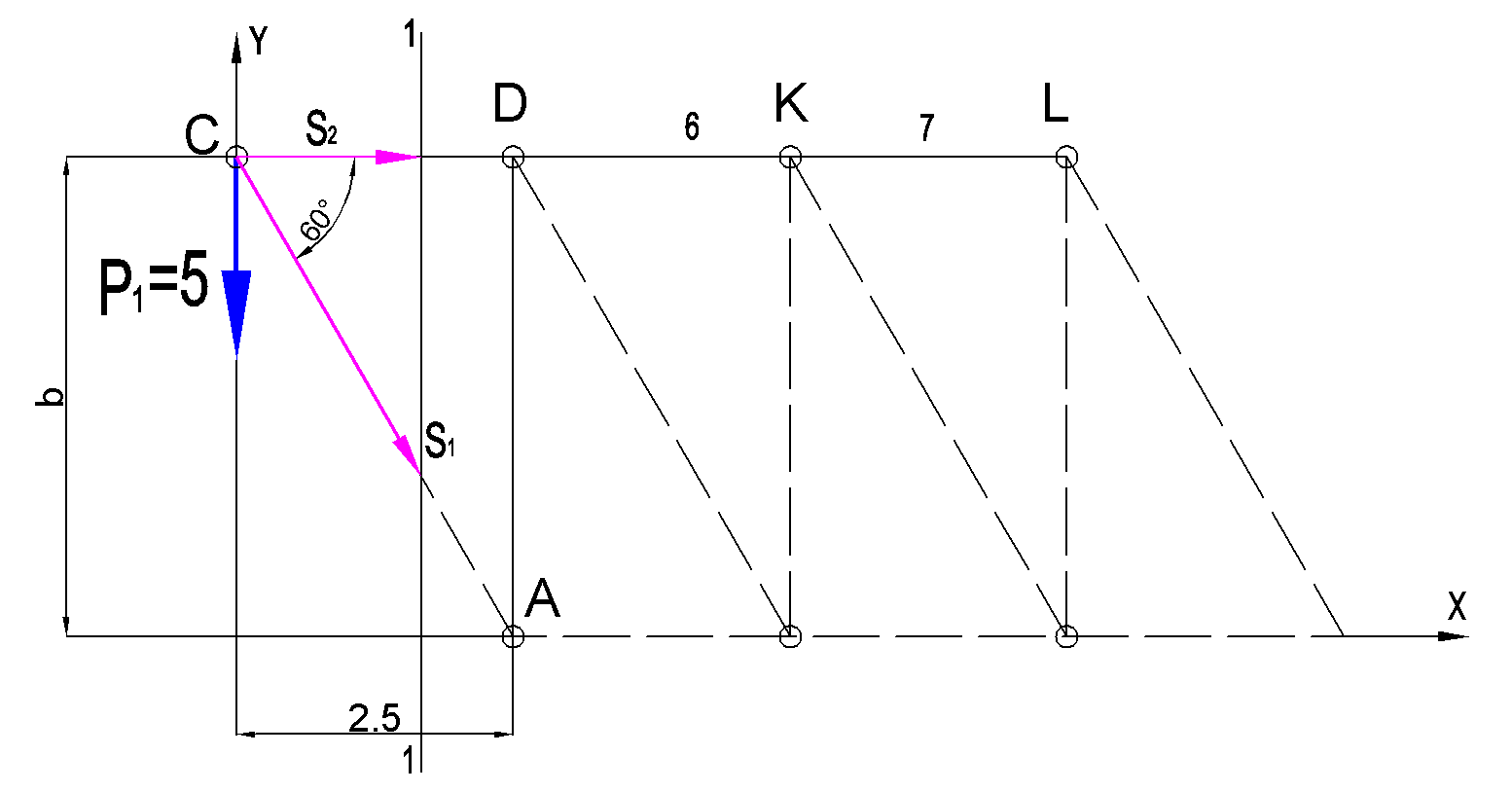 рис. 10 Для определения 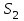 составляется уравнение моментов от сил, приложенных к оставшейся части фермы, относительно точки пересечения А (точка А). составляется уравнение моментов от сил, приложенных к оставшейся части фермы, относительно точки пересечения А (точка А).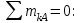 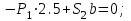 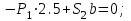 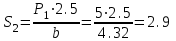 кН кН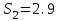 кН – что совпадает с вычисленным раннее кН – что совпадает с вычисленным раннееДля определения 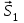 составляется уравнение моментов относительно точки L. составляется уравнение моментов относительно точки L.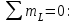 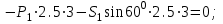 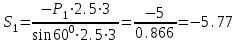 кН кН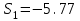 кН– что совпадает с вычисленным раннее кН– что совпадает с вычисленным раннее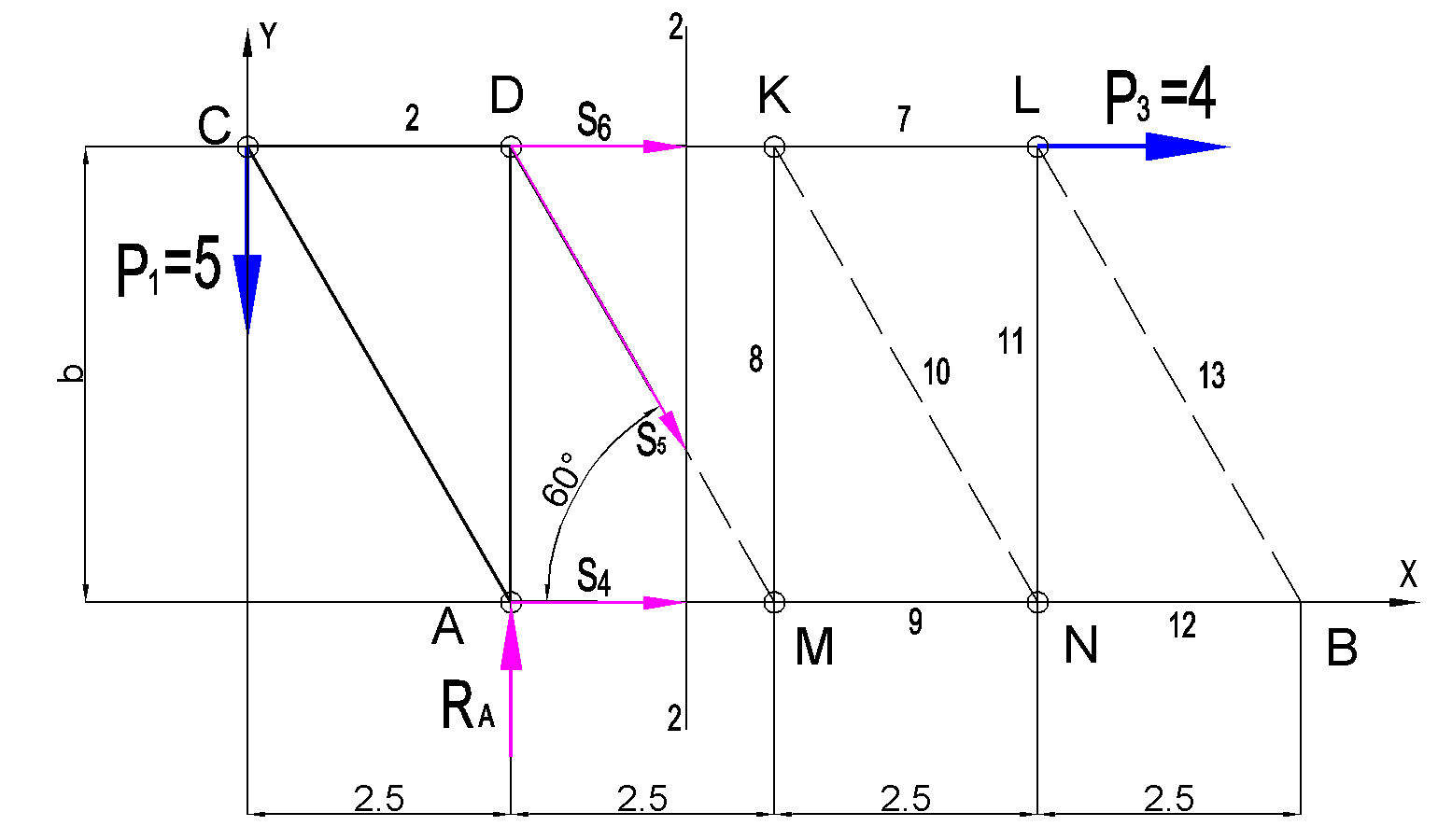 рис. 11 При определении 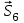 составляется уравнение моментов относительно точки M. составляется уравнение моментов относительно точки M.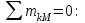 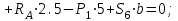 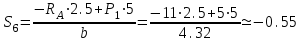 кН. кН.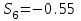 кН. – что совпадает с вычисленным раннее кН. – что совпадает с вычисленным раннееДля определения 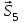 составляется уравнение моментов относительно точки L. составляется уравнение моментов относительно точки L.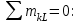 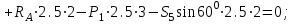 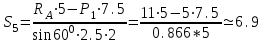 кН– что совпадает с вычисленным раннее кН– что совпадает с вычисленным раннеечто является дополнительной проверкой результатов счёта. Ответ: 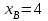 кН; кН; 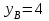 кН; кН; 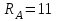 кН; стержни со знаком минус – сжаты, стержни со знаком плюс растянуты. кН; стержни со знаком минус – сжаты, стержни со знаком плюс растянуты. |
